В полярной системе координат основными постоянными элементами, по отношению к которым определяется положение точки на плоскости, является точка O - полюс и ось OP, которая называется полярной осью.
Если M - произвольная точка плоскости, не совпадающая с полюсом O, то ее положение на плоскости вполне определено заданием двух чисел: r - ее расстояния от полюса, выраженного в единицах масштаба, и 
- угла, на который следует повернуть полярную ось против часовой стрелки, чтобы она совпала с лучом OM. Числа r и называются полярными координатами точки M. Из них первой координатой считается r, а второй . Координата r называется полярным радиусом точки M (иногда радиус-вектором точки M), а координата - ее полярным углом (полярный угол измеряется в радианах). Полярные координаты записываются в скобках справа от ее обозначения, причем на первом месте в скобках записывается координата r, а на втором - координата , например,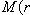 
. Полярный угол считается положительным, если он отсчитывается от полярной оси против часовой стрелки, и отрицательным, если он отсчитывается от полярной оси по часовой стрелке.
В определенной таким образом полярной системе координат полярный радиус r - всегда величина положительная или равная нулю (
), так как под r понимается расстояние от полюса O до точки M, а расстояние, как и всякая длина, не может быть отрицательным.
Однако на практике удобнее пользоваться такой системой полярных координат, в которой полярный радиус r может принимать и отрицательные значения. Система полярных координат, в которой полярный радиус r может принимать любые значения (положительные, отрицательные и равные нулю), называется обобщенной системой полярных координат. Этой системой мы и будем пользоваться.
Если точка M имеет координаты + r и 
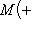
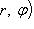, то она имеет также и координаты - r и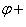 
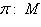
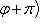, так как угол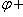 
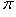характеризует направление полярного радиуса, прямо противоположное тому, которое соответствует углу .
Отметим, что какой бы из двух систем полярных координат мы не использовали, всегда паре чисел r и соответствует на плоскости единственная точка.
Если полюс полярной системы координат находится в начале прямоугольной системы координат, а положительная полуось Ox совпадает с полярной осью, ось же Oy перпендикулярна оси Ox и направлена так, что ей соответствует полярный угол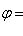 
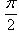, то по известным полярным координатам точки ее прямоугольные координаты вычисляются из формул
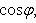
(1)
Если же известны прямоугольные координаты x и y точки, ее полярные координаты определяются по формулам
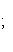
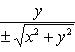
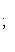
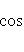
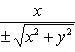
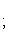(2)
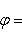
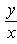
(3)
Как видно из (2), у корня в формуле для определения r стоят два знака - плюс и минус, что соответствует обобщенной системе полярных координат, а потому и в формулах для определения 
и 
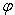перед корнем стоят два знака. Два знака в формуле для определения r появились потому, что r находится из выражения r 2 = x 2 + y 2. Если за r оставляется право быть только величиной положительной или нулем, то 
. Если же r, как это имеет место в обобщенной системе полярных координат, может быть и отрицательной величиной, то из r 2 = x 2 + y 2 следует, что 
.
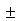
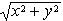В заключение укажем, как вести вычисления по формулам (2), чтобы по известным прямоугольным координатам точки найти ее полярные координаты. Прежде всего следует определить r, выбрав под корнем любой знак, затем вычислить и 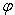, сохранив перед корнем в формулах (2) уже выбранный знак, и по знакам и 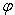установить четверть, в которой находится полярный угол . Само вычисление угла по таблицам тригонометрических функций следует вести по формуле (3).
Укажем также, как следует в полярной системе координат построить точку M по ее полярным координатам r и . По заданному полярному углу строим ось, проходящую через полюс под углом к полярной оси, причем положительное направление построенной оси должно совпадать с тем направлением, которое бы имела полярная ось, если бы ее повернули против часовой стрелки на угол . На этой оси откладываем отрезок длиной | r | от полюса O в положительном направлении построенной оси, если r > 0, и в отрицательном - если r < 0.
