Аналитическая геометрия и линейная алгебра. Теоретический курс.
Координаты точки на прямой и плоскости. Расстояние между двумя точками
Расстояние d между точками A (x 1) и B (x 2) на оси:


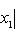

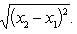
Величина AB (алгебраическая) направленного отрезка на оси:
AB = x 2 - x 1.
Если известны координаты концов отрезка прямой, то тем самым положение отрезка на плоскости вполне определено. Координаты точки записываются в скобках рядом с названием точки, причем всегда на первом месте в прямоугольной системе координат записывается абсцисса точки, а на втором - ее ордината. Например, если x 1 - абсцисса точки A, а y 1 - ее ордината, то это записывается так: A (x 1, y 1).
У точки, лежащей на оси абсцисс, ордината равна нулю; у точки, лежащей на оси ординат, абсцисса равна нулю. Обе координаты начала координат равны нулю.
Расстояние d между точками A (x 1, y 1) и B (x 2, y 2) плоскости определяется по формуле:

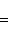
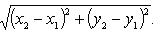
Проекции на оси координат направленного отрезка, или вектора  на плоскости с началом A (x 1, y 1) и концом B (x 2, y 2):
на плоскости с началом A (x 1, y 1) и концом B (x 2, y 2):





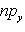



Тангенс угла между отрезком и положительным направлением оси Ox определяется по формуле (этот угол отсчитывается от оси Ox против часовой стрелки):
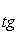




Определенный по этой формуле 
 является угловым коэффициентом прямой.
является угловым коэффициентом прямой.
Деление отрезка в заданном отношении. Координаты середины отрезка. Определение площади треугольника по известным координатам его вершин. Площадь многоугольника
1. Если x 1 и y 1 - координаты точки A, а x 2 и y 2 - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении 

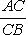 , определяются по формулам
, определяются по формулам








Если 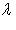
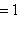 , то точка C (x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам
, то точка C (x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам





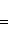


2. Площадь треугольника по известным координатам его вершин A (x 1, y 1), B (x 2, y 2), C (x 3, y 3) вычисляется по формуле





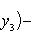



Полученное с помощью этой формулы число следует взять по абсолютной величине.
3. Площадь многоугольника с вершинами A (x 1, y 1), B (x 2, y 2), C (x 3, y 3),..., F (xn, yn) равна
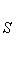










Выражение вида 
 равно x 1 y 2 - x 2 y 1 и называется определителем второго порядка.
равно x 1 y 2 - x 2 y 1 и называется определителем второго порядка.
Уравнение линии как геометрического места точек. Различные виды уравнений прямой. Исследование общего уравнения прямой. Построение прямой по ее уравнению
Уравнением линии называется уравнение с переменными x и y, которому удовлетворяют координаты любой точки этой линии и только они.
Входящие в уравнение линии переменные x и y называются текущими координатами, а буквенные постоянные - параметрами.
Чтобы составить уравнение линии как геометрического места точек, обладающих одинаковым свойством, нужно:
1) взять произвольную (текущую) точку M (x, y) линии;
2) записать равенством общее свойство всех точек M линии;
3) входящие в это равенство отрезки (и углы) выразить через текущие координаты точки M (x, y) и через данные в задаче.
В прямоугольных координатах уравнение прямой на плоскости задается в одном из следующих видов:






