Элементы теории корреляций

Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует определенной значение другой. Однако, в практической деятельности часто встречаются переменные величины, которые являются зависимыми, причем каждому значению одной из них соответствует не одно, а некоторое множество значений другой.

Переменные X и Y связаны статистически, если каждому значению одной из них соответствует распределение другой, меняющейся с изменением первой и по вариантам, и по частотам. Как правило, статистически зависимые величины задаются с помощью корреляционной таблицы:

y x	y ₁	y ₂	…	y_j	…	y_t	Всего
x ₁	n ₁₁	n ₁₂		n _{1 j}		n _{1 t}	n
x ₂	n ₂₁	n ₂₂		n _{2 j}		n _{2 t}	n
_…
x _i	n_i ₁	n_i ₂		n_ij		n_it	n

x_s	n_s ₁	n_s ₂		n_sj		n_st	n
Всего	n	n	…	n	…	n	n

Здесь частота n_ij показывает, что из n членов совокупности имеется n_ij таких, у которых переменная x принимает значения x_i, а переменная y – значения y_j.

Основными характеристиками корреляционной таблицы являются:

1. Общая средняя переменной X и переменной Y

;

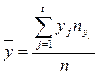
2. Дисперсия переменной X и переменной Y

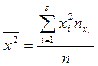
, где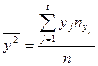

3. Групповые средние

, .

Групповые средние называются также математическими ожиданиями: – это математическое ожидание переменной Y, вычисленное в предположении, что переменная X приняла значение x; аналогично, .

Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием (групповой средней) другой. Корреляционная зависимость может быть представлена в виде

М_x (y)= f (x) (1) и M_y (x)=j(y) (2).

Уравнение (1) называется корреляционной зависимостью y на x; (2) – x на y. Эти уравнения называются также корреляционными уравнениями или уравнениями регрессии.

Для отыскания уравнения регрессии необходимо знать закон распределения двумерной случайной величины (X, Y). На практике исследователь располагает лишь выборкой пар значений (x_i, y_i) ограниченного объема. Поэтому можно говорить лишь об оценке (приближенном выражении) функций регрессии. Основными задачами регрессионного анализа являются:

1. установление формы и изучение зависимости между переменными, то есть вида функций (1) и (2). Предположение о виде этих функций можно сделать на основании эмпирических линий регрессии. Это ломаные, вершины которых находятся в точках (x_i, 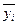) и (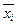, y_i) соответственно. Если обе функции линейные, то получим линейные корреляционные уравнения, а их графики называются прямыми регрессии.

2. оценка тесноты связи, то есть оценка степени рассеяния значений y около линии регрессии для разных значений x (или рассеяния значений x для разных значений y).

В случае линейной парной регрессии уравнения регрессии записываются в виде

и ,

где ; – коэффициенты регрессии y на x и x на y соответственно.

Важным числовым показателем зависимости пары случайных величин является значение ковариации их совместного распределения, а точнее, коэффициент корреляции.

Ковариация двух случайных величин

cov (X, Y) = m =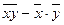

является величиной размерной, поэтому вместо нее обычно используют коэффициент корреляции. Коэффициент корреляции – это отношение ковариации к произведению средне квадратичных отклонений величин X и Y:

Коэффициент корреляции и коэффициенты регрессии взаимно связаны и взаимно выражаются друг через друга:

, ,

Коэффициент корреляции является показателем тесноты связи: чем ближе он к 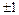, тем теснее связь, тем ближе значения Y расположены к прямой регрессии Y на X, а значения X к прямой X на Y. Коэффициент корреляции является показателем направления связи: если r >0, то связь между переменными прямая, то есть с увеличением одного фактора другой в среднем также увеличивается, если r <0, то связь между переменными обратная, то есть с увеличением одной переменной, другая в среднем уменьшается.

Упражнения.

9.1. Распределение 100 рабочих по стажу работы (X лет) и производительности труда (Y деталей/ч) дано в таблице:

Y X	5 – 10	10 - 15	15 - 20	20 – 25	25 - 30	Итого
1 – 3
3 – 5
5 – 7
7 – 9
9 – 11
Итого

Необходимо: 1) вычислить групповые средние и построить эмпирические линии регрессии; 2) найти уравнения прямых регрессии и построить их графики; 3) вычислить коэффициент корреляции; на уровне значимости a=0,05 оценить его достоверность и сделать вывод о тесноте и направлении связи между переменными X и Y; 4) оценить среднюю производительность рабочего со стажем 7 лет, используя соответствующие уравнения прямой регрессии.

9.2. Распределение 250 спортсменов по росту X(см) и весу Y(кг) дано в таблице:

Y X	60 – 70	70 – 80	80 - 90	90 – 100	100 - 110	Итого
165-170
170-175
175-180
180-185
185-190
190-195
Итого

Необходимо: 1) вычислить групповые средние и построить эмпирические линии регрессии; 2) найти уравнения прямых регрессии и построить их графики на том же чертеже; 3) вычислить коэффициент корреляции, на уровне значимости a=0,05 оценить его достоверность и сделать вывод о тесноте и направлении связи между переменными X и Y; 4) найти средний вес спортсмена ростом 180см, используя соответствующее уравнение регрессии.

9.3. Дано распределение 100 га земли по количеству внесенных удобрений X (ц/га) и по урожайности Y (ц/га):

Y X							Итого




Итого

Вычислить групповые средние и построить эмпирические линии регрессии; найти уравнения прямых регрессии и построить их графики на том же чертеже;

вычислить коэффициент корреляции, на уровне значимости a=0,05 оценить его достоверность и сделать вывод о тесноте и направлении связи; найти среднюю урожайность при внесении удобрений 20 ц/га.

9.4. Дано распределение 200 растений по массе каждого из них X(г) и по массе семян Y(г):

Y X						Итого





Итого

Найти групповые средние и построить групповые линии регрессии; вычислить коэффициент регрессии; вычислить коэффициент корреляции, решить вопрос о тесноте и направлении связи; составить уравнения прямых регрессии.

Варианты контрольных работ

Контрольная работа № 1

Вариант первый.

1. Найти предел: .

2. Найти производную функции: .

3. Найти уравнение касательной к кривой , которая перпендикулярна прямой 3y-x+3=0. Сделать чертеж.

4. Исследовать функцию y=x²(x-1)² и схематично построить ее график.

Вариант второй.

1. Найти предел: .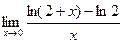

2. Найти производную функции: .

3. Составить уравнение касательной к графику функций y= , проведенной перпендикулярно прямой, проходящей через точки А(1;1) и В(3;-1). Сделать чертеж.

4. Исследовать функцию и схематично построить ее график.

Вариант третий.

1. Найти предел: .

2. Найти производную функции: .

3. Составить уравнение прямой, проходящей через вершину параболы y =2 x ²+6 x +4 перпендикулярно прямой x =-3. Сделать чертеж.

4. Исследовать функцию и схематично построить ее график.

Вариант четвертый.

1. Найти предел:

2. Найти производную функции: .

3. Составить уравнение касательной к графику функций y = , проведенной в точках пересечения его с прямыми x =1 и x =-1. Сделать чертеж.

4. Исследовать функцию и схематично построить ее график.

Вариант пятый.

1. Найти предел: .

2. Найти производную функции: .

3. Составить уравнения прямой, параллельно касательной к графику , проведенной в точке, которая является вершиной параболы y=x²+4x+5. Сделать чертеж.

4. Исследовать функцию и схематично построить ее график.

Вариант шестой.

1. Найти предел: .

2. Найти производную функции: .

3. Составить уравнения касательных к гиперболе , перпендикулярно прямой . Сделать чертеж.

4. Исследовать функцию и схематично построить ее график.

Вариант седьмой.

1. Найти предел: .

2. Найти производную функции:

3. Составить уравнения касательных к графику функции , параллельно прямой, проходящей через точки A(1;-2) и B(-1;3) Сделать чертеж.

4. Исследовать функцию и схематично построить ее график.

Вариант восьмой.

1. Найти предел: .

2. Найти производную функции: .

3. Найти уравнение касательной к параболе проходящей через левую точку пересечения параболы с прямой . Сделать чертеж.

4. Исследовать функцию и схематично построить ее график.

Вариант девятый.

1. Найти предел: .

2. Найти производную функции: .

3. Составить уравнения касательных к графику функции , проведенной перпендикулярно прямой, проходящей через точки и 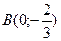. Сделать чертеж.

4. Исследовать функцию 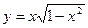и схематично построить ее график.

Вариант десятый

1. Найти предел: .

2. Найти производную функции: .

3. Составить уравнения прямой, проходящей через точку 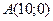, перпендикулярно касательной к графику функции , проведенной через точку пересечения его с осью абсцисс. Сделать чертеж.

4. Исследовать функцию и схематично построить ее график.

Контрольная работа № 2

Вариант первый.

5. Найти неопределенный интеграл:

6. Вычислить определенный интеграл:

7. Найти площадь фигуры, ограниченной линиями: , , . Сделать чертеж.

8. Исследовать сходимость ряда:

Вариант второй.

1. Найти неопределенный интеграл:

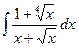
2. Вычислить определенный интеграл:

3. Найти площадь фигуры, ограниченной линиями: , 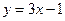. Сделать чертеж.

4. Исследовать сходимость ряда:

Вариант третий.

1. Найти неопределенный интеграл:

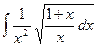
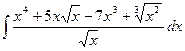
2. Вычислить определенный интеграл:

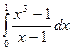
3. Найти площадь фигуры, ограниченной линиями , . Сделать чертеж.

4. Исследовать сходимость ряда по признаку сравнения:

Вариант четвертый.

1. Найти неопределенный интеграл:

2. Вычислить определенный интеграл:

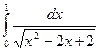
3. Найти площадь фигуры, ограниченной линиями 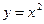, . Сделать чертеж.

4. Определить интервал сходимости ряда:

Вариант пятый.

1. Найти неопределенный интеграл:

2. Вычислить определенный интеграл:

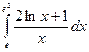
3. Найти площадь фигуры, ограниченной линиями , , . Сделать чертеж.

4. Исследовать сходимость ряда по признаку Даламбера: .

Вариант шестой.

1. Найти неопределенный интеграл:

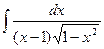
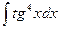
2. Вычислить определенный интеграл:

3. Найти площадь фигуры, ограниченной линиями , . Сделать чертеж.

4. Определить интервал сходимости ряда:

Вариант седьмой.

1. Найти неопределенный интеграл:

2. Вычислить определенный интеграл:

3. Найти площадь фигуры, ограниченной линиями , , , 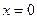. Сделать чертеж.

4. Исследовать сходимость ряда по признаку Даламбера:

Вариант восьмой.

1. Найти неопределенный интеграл:

2. Вычислить определенный интеграл:

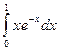
3. Найти площадь фигуры, ограниченной линиями 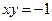, , 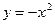. Сделать чертеж.

4. Разложить в ряд Маклорена функцию: ln(1+x)

Вариант девятый.

1. Найти неопределенный интеграл:

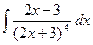
2. Вычислить определенный интеграл:

3. Найти площадь фигуры, ограниченной линиями , . Сделать чертеж.

4. Разложить в ряд Тейлора .

Вариант десятый.

1. Найти неопределенный интеграл:

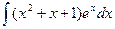
2. Вычислить определенный интеграл:

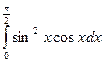
3. Найти площадь фигуры, ограниченной линиями 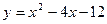, . Сделать чертеж.

4. Написать три первые члена ряда Маклорена для функции .

Контрольная работа № 3

Вариант первый.

1. В партии из 100 ламп имеется 30 бракованных. Наудачу отбираются 3 лампы. Найти вероятность того, что: 1) все 3 отобранные лампы бракованные; 2) среди отобранных ламп имеется одна бракованная.

2. В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30% - с заболеванием I и 20% -заболеванием М. Вероятность полного излечения болезни К равна 0,7; болезни I - 0,8 и болезни М - 0,9. Больной, поступивший в больницу был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К.

3. Стрелок поражает мишень с одинаковой вероятностью 2/3 в
каждом выстреле. Сделано три выстрела. Дискретная случайная
величина X- число попаданий в мишень. Найти закон распределения данной дискретной случайной величины X, а так же числовые характеристики (математическое ожидание, дисперсию и среднее квадратическое отклонение) этой случайной величины и построить многоугольник распределения.

4. По данным значениям величин x_i и y_i, предполагая наличие линейной зависимости между ними, установить тесноту этой связи, вычислив выборочный коэффициент корреляции, а также найти уравнение линейной регрессии Y на X _.Построить график вычисленной линейной зависимости и эмпирических точек.

x_i	1,0	1,2	1,3	1,4	1,5	1,6
y_i	17,0	21,5	22,0	23,8	25,0	26,5

Вариант второй

1. В пачке из 12 общих тетрадей имеется 7 тетрадей в клетку и 5 линейку. Наугад отобрано 6 тетрадей. Найти вероятность того, что:1) среди них будет одинаковое количество тетрадей в клетку и в линейку; 2) среди них будут тетради только в клетку.

2. В ящике сложены детали: 16 деталей с первого участка, 24 со второго и 20 с третьего. Вероятность того, что деталь, изготовленная на втором участке, отличного качества, равна 0,6 а для деталей,изготовленных на первом и третьем участках, эти вероятности равны 0,8. Найти вероятность того, что наудачу извлечённая деталь окажется отличного качества.

3. Брошены три монеты. Дискретная случайная величина X -
число выпадения герба при бросании трех монет. Найти закон распределения данной дискретной случайной величины X, а так же числовые характеристики (математическое ожидание, дисперсию и среднее квадратическое отклонение) этой случайной величины и построить многоугольник распределения.

x_i	1,0	1,2	1,4	1,6	1,8	2,0
y_i	0,9	1,8	2,1	2,9	3,3	3,4

Вариант третий

1. В коробке имеется 5 одинаковых изделий, причем 3 из них окрашены. Наудачу вынуты 2 изделия. Найти вероятность того, что среди вынутых изделий: 1) одно окрашенное; 2) оба окрашенных.

2. В одной урне 5 белых и 6 черных шаров, а в другой урне 4 белых и 8 черных шаров. Из первой урны наудачу вынимают 3 шара опускают во вторую урну. После этого из второй урны наудачу вынимают 4 шара. Найти вероятность того, что все вынутые из второй урны шары - белые.

3. Устройство состоит из трех независимо работающих элементов. Вероятность безотказной работы в течении определенного периода времени для первого элемента равна 0,8; для второго - 0,6;
для третьего -- 0,5. Дискретная случайная величина X - число элементов устройства, безотказно работающих в течении данного периода времени. Найти закон распределения данной дискретной случайной величины X, а так же числовые характеристики (математическое ожидание, дисперсию и среднее квадратическое отклонение) этой случайной величины и построить многоугольник распределения.

x_i	0,2	0,6	1,0	1,4	1,8	2,2
y_i	4,5	8,5	11,0	12,8	17,0	18,0

Вариант четвертый

1. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди вынутых деталей: 1) нет бракованных; 2) нет годных.

2. В первом ящике имеются 8 белых и 6 чёрных шаров, а во втором 10 белых и 4 чёрных. Наугад выбирают ящик и шар. Известно, что вынутый шар чёрный. Найти вероятность того, что был выбран первый ящик.

3. В урне 4 белых и 8 черных шаров. Вынули два шара. Дискретная случайная величина X- число вынутых белых шаров. Найти закон распределения данной дискретной случайной величины X, а так же числовые характеристики (математическое ожидание, дисперсию и среднее квадратическое отклонение) этой случайной величины и построить многоугольник распределения.

x_i
y_i	3,2	7,8	11,2	13,0	19,1	23,6

Вариант пятый

1. В ящике 30 исправных предохранителей и 5 с дефектами. Необходимо заменить 3 предохранителя, которые выбираются наудачу их ящика. Найти вероятность того, что: 1) все 3 выбранных предохранителя исправны; 2) один предохранитель оказался с дефектом.

2. Из двух близнецов первым родился мальчик. Какова вероятность того, что вторым тоже родится мальчик, если среди близнецов вероятность рождения двух мальчиков равна p, а вероятность рождения двух девочек равна q, а для разнополых близнецов вероятность родиться первым для обоих полов одинакова?

3. Брошено три игральных кости. Дискретная случайная величина X— число появления шестерки. Найти закон распределения данной дискретной случайной величины X, а так же числовые характеристики (математическое ожидание, дисперсию и среднее квадратическое отклонение) этой случайной величины и построить многоугольник распределения.

x_i	-0,2	0,3	0,6	0,9	1,1	1,4
y_i	-0,3	0,5	0,8	2,0	2,1	3,1

Вариант щестой

1. В урне находятся 3 белых, 4 черных и 5 красных шаров. Найти вероятность того, что: 1) вынутый наудачу шар белый; 2)вынутый наудачу шар черный; 3) вынутый наудачу шар желтый; 4)вынутый наудачу шар красный; 5) среди двух вынутых наудачу шаров один будет белым.

2. Из 18 стрелков 5 попадают в мишень с вероятностью 0,8; 7 -с вероятностью 0,7; 4 - с вероятностью 0,6 и 2 - с вероятностью 0,5. Наудачу выбранный стрелок не попал в мишень. К какой группе вероятнее всего принадлежал этот стрелок? (Найти условные вероятности всех-гипотез).

3. Вероятность того, что саженец груши приживется равна 0,8; яблони - 0,9. Куплено два саженца груши и один - яблони. Дискретная случайная величина X -число прижившихся саженцев. Найти закон распределения данной дискретной случайной величины X, а так же числовые характеристики (математическое ожидание, дисперсию и среднее квадратическое отклонение) этой случайной величины и построить многоугольник распределения.

x_i	0,5	1,0	2,0	2,7	3,5	4,0
y_i	3,8	5,8	6,9	9,8	10,3	13,1

Вариант седьмой

1. В группе 12 студентов, среди которых 8 отличников. По списку наугад отобрано 9 студентов. Найти вероятность того, что среди отобранных студентов: 1) 5 отличников; 2) 8 отличников.

2. При переливании крови надо учитывать группу крови донора и больного. Человеку, имеющему четвертую группу крови, можно перелить кровь любой группы; человеку со второй или третьей группой крови можно перелить кровь либо той же группы, либо первой; человеку с первой группой крови можно перелить кровь только первой группы. Среди населения города 33,7% имеют первую группу крови, 37,5% - вторую, 20,9% - третью, 7,9% - четвертую. Найти вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора.

3. Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания в мишень для первого стрелка равна 0,5, для второго - 0,4. Дискретная случайная величина X – число попаданий в мишень. Найти закон распределения данной дискретной случайной величины X, а так же числовые характеристики (математическое ожидание, дисперсию и среднее квадратическое отклонение) этой случайной величины и построить многоугольник распределения.

x_i	-3	-2	-1	0,1
y_i	11,2	3,9	0,8	-5,1	-5,7	-10,1

Вариант восьмой

1. В урне находятся 12 белых и 8 красных шаров. Найти вероятность того, что: 1) среди двух вынутых наудачу шаров будет один белый шар; 2) среди вынутых наудачу 8 шаров будет 3 красных.

2. На двух автоматах производятся одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата втрое больше производительности второго. Первый автомат в среднем производит 80% деталей первого сорта, а второй - 90%. Взятая наудачу с конвейера деталь оказалась первого сорта. Найти вероятность того, что эта деталь произведена первым автоматом.

3. В партии из 6 деталей имеется 4 стандартных. Наудачу отобрано три детали. Дискретная случайная величина X – число стандартных деталей среди отобранных. Найти закон распределения данной дискретной случайной величины X, а так же числовые характеристики (математическое ожидание, дисперсию и среднее квадратическое отклонение) этой случайной величины и построить многоугольник распределения.

x_i	0,3	0,8	1,2	1,7	2,2	2,7
y_i	0,7	1,7	1,6	3,1	3,3	4,6

Вариант девятый

1. В цехе работают 6 мужчин и 4 женщины. Наудачу отбираются 7 человек. Найти вероятность того, что среди отобранных
будет: 1)3 женщины; 2) 6 мужчин.

2. Агентство по страхованию автомобилей разделяет водителей по трем классам: класс H₁, (мало рискует), класс H₂ (рискует средне), класс H₃ (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат к кассу H₁ 50% - к классу H₂, 20% - к классу H₃. Вероятность того, что в течение года водитель класса H₁, попадет в хотя бы одну аварию, равна 0,01; для водителя класса H₂ - 0,02; для водителя класса H₃ - 0,08. Некоторый водитель страхует свою машину и в течение года попадает в аварию. Найти вероятность того, что этот водитель принадлежит классу: 1)H₁; 2)H₂; 3)H₃.

3. Улов состоит из 60 рыб, среди которых 10 имеют вес, меньший требуемого. Наугад отобрано пять экземпляров. Дискретная случайная величина X - число отобранных рыб, имеющих вес меньше требуемого. Найти закон распределения данной дискретной случайной величины X, а так же числовые характеристики (математическое ожидание, дисперсию и среднее квадратическое отклонение) этой случайной величины и построить многоугольник распределения.

x_i	1,1	1,3	1,5	1,6	1,9	2,1
y_i	2,6	5,0	5,4	6,1	6,6	7,9

Вариант десятый

1. Устройство состоит из 5 элементов, из которых 2 изношены. При включении устройства случайным образом включаются 2 элемента. Найти вероятность того, что: 1) включенными окажутся неизношенные элементы; 2) включатся один изношенный и один неизношенный

2. Имеются три партии деталей по 30 штук в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 30, 25 и 20. Из произвольно выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию, а затем вторично наудачу извлекают деталь, которая также оказывается стандартной. Найдите вероятность того, что детали были извлечены из третьей партии.

3. На пути движения лосося к месту нереста находится 4 шлюза. Вероятность прохода лосося через каждый шлюз равна 3/5. Дискретная случайная величина X -- число шлюзов, пройденных лососем до первого задержания у шлюза. Найти закон распределения данной дискретной случайной величины X, а так же числовые характеристики (математическое ожидание, дисперсию и среднее квадратическое отклонение) этой случайной величины и построить многоугольник распределения.

x_i	1,0	1,1	1,3	1,5	1,6	1,7
y_i	16,5	21,5	22,0	24,0	24,5	27,0

Контрольные тесты