Выборочный метод исследования – метод, позволяющий по результатам изучения сравнительно небольшой части всей совокупности получить с достаточной для практики достоверностью необходимую информацию.
Различные значения признака, встречающиеся у членов совокупности, называются вариантами (xi). Число, показывающее с6колько раз вариант встречается в совокупности, называется частотой (ni).
Вариационным рядом называется ранжированным (то есть расположенный в порядке возрастания и убывания) ряд вариантов с соответствующими частотами.
Вариационный ряд называется дискретным, если значения признака отличаются друг от друга на некоторую постоянную величину, и непрерывным, если значения признака могут отличаться на сколь угодно малую величину.
Графически вариационные ряды изображают в виде полигона и гистограммы.
Полигон, как правило, служит для изображения дискретного вариационного ряда и представляет собой ломаную, вершины которой имеют координаты (xi, ni).
Гистограмма служит только для изображения интервальных вариационных рядов и представляет собой фигуру из прямоугольников с основаниями, равными интервальным разностям и высотами, равными частотам.
Основными характеристиками вариационного ряда являются: средняя арифметическая 
, дисперсия 
, среднее квадратическое отклонение s =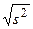 
.
Упрощенные формулы вычисления характеристик:
, 
,
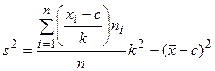где C – значение варианты с наибольшей частотой; k – наибольший общий делитель разностей xi-C.
Эмпирические числовые характеристики выборки считаются точечными оценками этих же характеристик всей генеральной совокупности.
Точечной оценкой генеральной средней (математического ожидания) является выборочная средняя 
. При достаточно большом объеме выборки n выборочную среднюю можно с достаточной степенью точности считать нормально распределенной случайной величиной с параметрами M (X)= a, σ(X)= 
, где – среднее квадратическая ошибка выборки, она вычисляется по одной из следующих формул в зависимости от цели и вида выборки.
| Цель | Выборка | |
| Повторная | Бесповторная | |
| для средней | 
| 
|
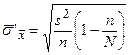
| для доли |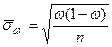 
| 
|
Доверительная вероятность определяется по формуле P (| X – a |≤Δ)=Ф(Δ/σ).
Если обозначить Δ/σ= t, то предельная ошибка выборки Δ= t .
Зная предельную ошибку выборки, можно найти ( –Δ; +Δ) – доверительный интервал для генеральной средней, или (ω–Δ; ω+Δ) – доверительный интервал для генеральной доли.
Необходимый объем выборки при фиксированных предельной ошибке Δ и доверительный вероятности p вычисляется в зависимости от вида и цели выборки по одной из следующих формул:
| Цель | Выборка | |
| Повторная | Бесповторная | |
| для средней | 
| 
|
| для доли | 
| 
|
Если объем генеральной совокупности не задан, то либо в условии задачи указывается, что N значительно превосходит n, либо это выясняется из содержания задачи. В таких случаях, полагая N →∞, получим 1– n / N →1, тогда 
, 
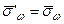. Это значит, что расчетные формулы для повторной и бесповторной выборок будут одинаковыми.
Заметим, что при одних и тех же точности и надежности оценок объем бесповторной выборки n ' всегда меньше объема повторной выборки n. Этим объясняется тот факт, что на практике, в основном, используется бесповторная выборка.
Пример. Для определения средней заработной платы 200 рабочих совхоза по схеме собственно-случайной бесповторной выборки было отобрано 50 рабочих. Результаты выборки приведены в таблице:
| Зарплата, руб. | 1000-1800 | 1800-2600 | 2600-3400 | 3400-4200 | свыше 4200 | Всего |
| Число рабочих | 4 | 6 | 20 | 12 | 8 | 50 |
Найти: 1)вероятность того, что средняя заработная плата всех рабочих совхоза отличается от средней заработной платы в выборке не более, чем на 100 рублей по абсолютной величине;
2)границы, в которых с вероятностью 0,869 заключена доля рабочих совхоза, имеющих заработную плату не менее 3000 рублей;
3)каким должен быть объем выборки, чтобы с вероятностью 0,9011 можно было утверждать, что отклонение средней заработной платы всех рабочих совхоза от средней заработной платы в выборке составит не более 150 рублей.
Решение. Найдем основные характеристики выборки по упрощенным формулам для чего составим таблицу вспомогательных расчетов (предварительно проведя «замыкание» вариационного ряда и переходя к дискретному распределению).
| xi | ni | xi – c | 
| 
| 
|
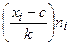
| -1600 -800 | -2 -1 | -8 -6 | 16 6 0 12 32 | ||
| Всего | 50 | 14 | 66 |
Возьмем c =3000, k =800. Используя упрощенные формулы, найдем
(руб) – средняя заработная плата рабочих в выборке,
- дисперсия,
s = 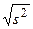≈891,42 (руб) – среднее квадратичное отклонение.
1) Вероятность того, что средняя заработная плата всех рабочих совхоза отличается от средней заработной платы в выборке не более, чем на 100 рублей, найдем по формуле доверительной вероятности P (| X-a |≤Δ)=Ф(Δ/σ), где Δ=100, a = =3224, 
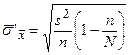= , n =50, N =200, s 2=794624,
≈109,18,
P =Ф(100/109,18)=Ф(0,92)=0,6424.
2) Для того, чтобы найти доверительный интервал для генеральной доли, найдем долю рабочих в выборке, у которых заработная плата не менее 3000 рублей:
,
предельная ошибка выборки Δ= t 
, где t найдем из условия P =Ф(t)=0,869, откуда t =1,51, а величина
= 
=0,049.
Следовательно, Δ=1,51∙0,49≈0,07, а доверительный интервал имеет границы (ω–Δ;ω+Δ)=(0,8–0,07;0,8+0.07)=(0.73;0,87).
1) Необходимый объем выборки , где ; по условию P =Ф(t)=0,9011, значит t =1,65; Δ=150. Имеем 
, 
(человек).
Упражнения.
8.1. Для определения средней зарплаты 1000 учителей города было отобрано выборочным путем 100 учителей. Полученное при обследовании распределение приведено в таблице:
| Зарплата, тыс.руб | 500 – 1000 | 1000 - 1500 | 1500 - 2000 | 2000 –2500 | 2500 - 3000 | Свыше 3000 | Итого |
| Число учителей |
Найти: 1) границы, в которых с вероятностью 0,95 заключена средняя зарплата учителей города; 2) определить, каким должен быть объем выборки, чтобы те же границы можно было гарантировать с вероятностью 0,99? 3) вероятность того, что в данном городе доля учителей, зарплата которых более 2000 рублей, отличается от доли таких учителей в выборке не более, чем не 5%. (Выборка бесповторная).
8.2. Результаты обследования 50 человек из группы мигрирующего населения по их возрасту приведены в таблице:
| Возраст мигрирующего населения, лет | До 30 | 30-40 | 40-50 | 50-60 | Свыше 60 | Итого |
| Количество человек |
Найти: 1) границы, в которых с вероятностью 0,9949 заключен средний возраст всего мигрирующего населения, если объем генеральной совокупности велик по сравнению с объемом выборки; 2) вероятность того, что доля мигрантов в возрасте до 40 лет в выборке отличается от доли их во всей генеральной совокупности не более, чем на 0,05 (по абсолютной величине).
8.3. С земельного массива в 8000 га путем бесповторного отбора получены данные об урожайности гречихи:
| Урожайность, ц/га | 11-12 | 12-13 | 13-14 | 14-15 | 15-16 | 16-17 | Всего |
| Число га |
Найти: 1) вероятность того, что средняя урожайность на всем массиве отличается от средней выборочной не более, чем на 0,08 ц/га (по абсолютной величине); 2) границы, в которых с вероятностью 0,9512 заключена доля гектаров с урожайностью не менее 14 ц; 3) каким должен быть объем выборки, чтобы с вероятностью 0,992 гарантировать те же границы для доли гектаров с урожайностью не менее 14 ц.
8.4. По схеме собственно-случайной бесповторной выборки было отобрано 100 студентов из 500 обучающихся и получены следующие данные о времени решения задачи по теории вероятностей:
| Время решения задачи, мин | 5-8 | 8-11 | 11-14 | 14-17 | 17-20 | Итого |
| Количество студентов |
Найти: 1) вероятность того, что среднее время решения задачи в выборке отличается от времени решения задачи во всей генеральной совокупности не более чем на 1 мин (по абсолютной величине); 2) число студентов, которое нужно отобрать в выборку, чтобы то же отклонение гарантировать с вероятностью 0,9876; 3) границы, в которых с вероятностью 0,9596 заключена доля студентов, решавших задачу не более 11 мин.
8.5. С лесного массива, насчитывающего 20 000 взрослых деревьев, с помощью выборочного метода были получены следующие данные:
| Количество деловой древесины, м3 | 0,4-0,6 | 0,6-0,8 | 0,8-1,0 | 1,0-1,2 | 1,2-1,4 | 1,4-1,6 | Итого |
| Число деревьев |
Найти: 1) вероятность того, что среднее количество древесины в одном дереве во всем лесном массиве и в выборке отличается по абсолютной величине не более чем на 0,02 м3; 2) границы, в которых с вероятностью 0,992 заключено среднее количество деловой древесины в дереве; 3) определить, каким должен быть объем выборки, чтобы те же границы можно было гарантировать с вероятностью 0,899?
