Тригонометрические функции острого угла в прямоугольном треугольнике

И их значения от некоторых углов.

Обозначим угол А соответствующей греческой буквой α.

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет а, лежащий напротив угла α, называется противолежащим (по отношению к углу α).

Другой катет b, который лежит на одной из сторон угла α, называется прилежащим (по отношению к углу α).

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

Значения тригонометрических функций некоторых углов

 

	300	450	600

Задания с решением

1. В треугольнике ABC угол C равен 90º, ВС=4, 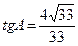. Найдите AB.

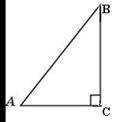Решение:

 

 

tgA= 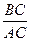; тогда откуда АС= .

По теореме Пифагора АС² +ВС² =АВ².

АВ² = 33+16, АВ = 7

Ответ: 7

2. В треугольнике ABC угол C равен 90º, AB= , АС=8. Найдите tg A.

Решение:

По теореме Пифагора АС² +ВС² =АВ². 8² +ВС² =()²

ВС²=80-64 ВС²=16 ВС=4

tgA= =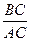

Ответ: 0,5

3. В треугольнике ABC угол C равен 90º, CH – высота, AB=27, . Найдите BH.

Решение:

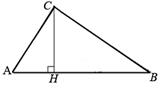
В треугольнике АВС 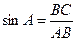. Тогда , откуда ВС=18

Угол А равен углу СНВ. Тогда в треугольнике СНВ то есть 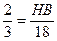откуда НВ=12.

Ответ: 12

 

4. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на .

Решение:

Достроим угол АОВ до треугольника ОВА. Из рисунка видно, что ОВ=ВА, как гипотенузы равных треугольников, ВК делит основание ОА пополам, значит ВК – медиана, а значит и высота.

Из рисунка по теореме Пифагора находим , , 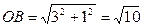тогда .

В ответ надо записать

Ответ: 2

Задания для самостоятельного решения

 

1. В треугольнике ABC угол C равен 90º, AB = 25, BC = 20. Найдите cosA.

 

2. В треугольнике ABC угол C равен 90º, AB = 25, BC = 20. Найдите sinA.

3. В треугольнике ABC угол C равен 90º, CH – высота, АВ = 27, 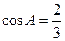Найдите AH.

4. В треугольнике ABC AC= BC=5, . Найдите высоту CH.

5. Найдите тангенс угла AOB.

6. Найдите тангенс угла С, если стороны квадратных клеток равны .

Занятие 4

Многоугольники. Сумма углов выпуклого многоугольника

Параллелограмм, прямоугольник, ромб, квадрат. Основные понятия и свойства.

 

Многоугольник — это геометрическая фигура, ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех и более отрезков (звеньев).

Выпуклым многоугольником называется многоугольник, обладающий тем свойством, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины

 

ТЕОРЕМА Сумма углов выпуклого n -угольника равна 180° (n -2), где n – число сторон

 

Параллелограмм. Основные понятия и свойства.

Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

СВОЙСТВА ПАРАЛЛЕЛОГРАММА

ТЕОРЕМА. Во всяком параллелограмме противоположные углы равны.

ТЕОРЕМА. Во всяком параллелограмме противоположные стороны равны.

ТЕОРЕМА. Во всяком параллелограмме диагонали делятся в точке пересечения пополам.

ТЕОРЕМА. Во всяком параллелограмме диагональ делит его на два равных треугольника.

ТЕОРЕМА. Во всяком параллелограмме сумма углов, прилежащих к одной стороне равна 180°.

ТЕОРЕМА. Во всяком параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его сторон.

ТЕОРЕМА. Точка пересечения диагоналей параллелограмма есть его центр симметрии.

 

ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА

ТЕОРЕМА. Если в четырехугольнике противоположные стороны попарно равны, то такой четырехугольник параллелограмм.

ТЕОРЕМА. Если в четырехугольнике две противоположные стороны равны и параллельны, то такой четырехугольник параллелограмм.

ТЕОРЕМА. Если в четырехугольнике диагонали делятся в точке пересечения пополам, то такой четырехугольник параллелограмм.

Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.