Прямоугольник — это параллелограмм, у которого все углы прямые.
СВОЙСТВА И ПРИЗНАКИ ПРЯМОУГОЛЬНИКА
Прямоугольник обладает всеми свойствами и ему присущи все признаки параллелограмма,
кроме того:
ТЕОРЕМА. В прямоугольнике диагонали равны.
ТЕОРЕМА. Если в параллелограмме диагонали равны, то такой параллелограмм является прямоугольником.
Ромб и его свойства
По определению, ромб – это параллелограмм, все стороны которого равны.
СВОЙСТВА И ПРИЗНАКИ РОМБА
ТЕОРЕМА. Диагонали ромба взаимно перпендикулярны.
ТЕОРЕМА. Если в параллелограмме диагонали взаимно перпендикулярны, то параллелограмм является ромбом.
ТЕОРЕМА. Диагонали ромба делят его углы пополам.
ТЕОРЕМА. Если в параллелограмме диагонали делят его углы пополам, то параллелограмм является ромбом.
ТЕОРЕМА. Каждая диагональ ромба является его осью симметрии.
Кроме того, ромб обладает всеми свойствами параллелограмма.
Квадрат и его свойства
Квадрат – это прямоугольник, у которого все стороны равны. Можно дать и другое определение квадрата: квадрат – это ромб, у которого все углы прямые.
Квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Задания с решением
1. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Решение:
Пусть ВМ и СК – биссектрисы углов параллелограмма, прилежащих к стороне ВС. Сумма углов АВС и BCD равна 180°. Углы ОВС и ОСВ – половинки углов АВС и ВСD. Значит, сумма углов АВС и ВСD равна 90°. Из треугольника ВОС находим, что угол ВОС – прямой.
Ответ: 90°.
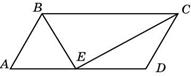2. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 12. Найдите его большую сторону.
Решение:
Углы СВЕ и ВЕА, а также СЕD и ВСЕ — накрест лежащие. Накрест лежащие углы равны. Значит, 
СВЕ = ВЕА, а угол СЕD = ВСЕ. Получаем, что треугольники АВС и CDE — равнобедренные, то есть АЕ = АВ, а DЕ = CD. Тогда AD = 12+12 = 24.
Ответ: 24
3. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 8. Найдите диагональ данного прямоугольника.
Решение:
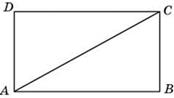
Пусть СВ =8. Тогда из того, что угол прямоугольника равен 90º и разделен в отношении 1:2, следует, что ДАС = 60º, а САВ =30º. Катет, лежащий против угла в 30º, равен половине гипотенузы, следовательно АС = 2 СВ = 2·8=16.
Ответ: 16.
4. Найдите меньшую диагональ ромба, стороны которого равны 2, а острый угол равен 60°.
Решение:
Проведем меньшую диагональ ромба DВ и рассмотрим треугольник ADB.
Поскольку AD = АB =2 как стороны ромба, то треугольник равнобедренный. А поскольку угол DAB равен 60°, то треугольник ADB – равносторонний. Следовательно, меньшая диагональ ромба равна.
Ответ: 2
5. Найдите высоту ромба, сторона которого равна 
, а тупой угол равен 120°.
Решение:
Если тупой угол равен 120°, то острый угол равен 60°.
Пусть А=60°. Из треугольника АDH следует: 
. Получаем 
.
Тогда 
. Откуда DH = 
Ответ: 3
6. Диагонали ромба относятся как 3:4. Периметр ромба равен 120. Найдите диагонали ромба.
Решение:
По условию АС:ВD=3:4=6:8. Тогда АС= 6х и BD=8х.
Диагонали ромба перпендикулярны и делятся точкой пересечения пополам, значит, треугольник АОВ – прямоугольный и АО= 3 х и BО = 4 х.
По теореме Пифагора АВ2 = АО2 + ОВ2
Так как периметр равен 120, а все стороны ромба равны, то АВ = 120: 4 = 30
Получаем: 
900= 
Откуда 
, 
. Тогда АС = 6·6=36 и BD =8·6=48.
Ответ: 36 и 48.
7. Внутренние углы выпуклого четырехугольника относятся как 2: 2, 5: 9, 5: 10. Найти меньший угол.
Решение:
Сумму внутренних углов четырехугольника вычисляем по формуле 180° (n – 2), где число сторон n = 4. Получаем 180° (4 – 2) = 360°. Из отношения углов 2:2, 5:9, 5:10 получаем, что углы равны 2 х, 2,5 х, 9,5 х и 10 х. Получаем уравнение: 2 х +2,5 х +9,5 х +10 х =360°, 24 х = 360°, х = 15°.
Меньший угол равен 2 х, то есть 2·15°=30°
Ответ: 30°
