ПРИЗНАК № 1. Если две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу, заключенному между ними, другого треугольника, то такие треугольники равны.
ПРИЗНАК № 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
ПРИЗНАК № 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Свойства равнобедренного треугольника
ТЕОРЕМА. В равнобедренном треугольнике биссектриса угла при вершине есть одновременно и медиана, и высота.
ТЕОРЕМА. Углы при основании равнобедренного треугольника равны.
ТЕОРЕМА. В равнобедренном треугольнике биссектрисы углов при основании равны.
ТЕОРЕМА. В равнобедренном треугольнике высоты, проведенные к боковым сторонам, равны.
ТЕОРЕМА. В равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
ТЕОРЕМА. В равнобедренном треугольнике отрезок, соединяющий основания биссектрис, проведенных к боковым сторонам, параллелен основанию.
ТЕОРЕМА. В равнобедренном треугольнике отрезок, соединяющий основания высот, проведенных к боковым сторонам, параллелен основанию.
Признаки равнобедренного треугольника
ТЕОРЕМА. Если в треугольнике два угла равны, то он равнобедренный.
ТЕОРЕМА. Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
ТЕОРЕМА. Если в треугольнике высота является и биссектрисой, то такой треугольник равнобедренный.
ТЕОРЕМА. Если в треугольнике медиана является и биссектрисой, то такой треугольник равнобедренный.
ТЕОРЕМА. Если в треугольнике две высоты равны, то треугольник равнобедренный.
ТЕОРЕМА. Если в треугольнике две медианы равны, то треугольник равнобедренный.
ТЕОРЕМА. Если в треугольнике две биссектрисы равны, то треугольник равнобедренный.
Задания с решением
1. В треугольнике ABC угол C равен 45°, AD – биссектриса, угол CAD равен 30°. Найдите угол B.

Решение:
Рассмотрим треугольник ABC. Поскольку AD – биссектриса, то углы BAD и CAD равны:
 BAD =
BAD =  CAD = 30°. С другой стороны, угол
CAD = 30°. С другой стороны, угол  BAC =
BAC =  BAD +
BAD +  CAD = 30° + 30° = 60°. Но сумма углов треугольника равна 180°. Поэтому имеем:
CAD = 30° + 30° = 60°. Но сумма углов треугольника равна 180°. Поэтому имеем:
A + B + C = 180°;
60° + B + 45° = 180°;
B = 75°.
Ответ: 75º
2. В треугольнике ABC стороны AC = BC, угол C равен 40°. Найдите внешний угол DBC.
Решение:

По условию, треугольник ABC — равнобедренный: AC = BC. Следовательно, углы при основании равны:  A =
A =  ABC = x. Но сумма углов треугольника равна 180°, поэтому:
ABC = x. Но сумма углов треугольника равна 180°, поэтому:
 A +
A +  ABC +
ABC +  C = 180°;
C = 180°;
x + x + 40° = 180°;
2 x = 140°;
x = 70°.
Итак, угол ABC равен 70°. Углы ABC и DBC — смежные, поэтому их сумма равна 180°. Имеем:
 ABC +
ABC +  DBC = 180°;
DBC = 180°;
70° +  DBC = 180°;
DBC = 180°;
 DBC = 110°.
DBC = 110°.
Ответ: 110°
3. В треугольнике ABD угол A равен 48°, а угол АCВ равен 56°. BD = BC. Найдите угол D.
Решение:

В треугольнике BCD BD = BC, поэтому он равнобедренный и углы D и BCD равны, то есть
 D =
D =  BCD = x.
BCD = x.
 ACD =
ACD =  ACB +
ACB +  DCB = 56° + x.
DCB = 56° + x.
Рассмотрим треугольник ADC. В нем сумма углов равна 180°, поэтому:
Ð A + Ð D +Ð ACD = 180°;
48° + x + 56° + x = 180°;
2 x + 104° = 180°;
2 x = 76°;
x = 38°.
Ответ: 38°
4. Отрезок, соединяющий середины сторон AС и ВC треугольника ABC, на 3 см меньше стороны АВ, на 2 см меньше стороны AC и на 1 см меньше стороны СB. Найдите периметр треугольника ABC.
Решение:

По определению ED – средняя линия. Тогда по свойству средней линии AB = 2 ED.
Пусть ED = х, тогда АВ = 2 х. По условию: ED = АВ – 3, ED = AС – 2, ED = СB – 1.
Получаем: х = 2х – 3, откуда х = 3, то есть ED = 3. Тогда АС = 5, СВ = 4. Периметр треугольника АВС равен сумме длин сторон АВ, ВС и АС. То есть  .
.
Ответ: 12см
5. В равнобедренном треугольнике сумма двух углов равна 80°.Найти углы треугольника.
Решение:

Так как треугольник равнобедренный, то углы А и В равны.
Возможны два случая:  А +
А +  В = 128° или
В = 128° или  А +
А +  С = 128°
С = 128°
1) Если  А =
А =  В = х и
В = х и  А +
А +  В = 128°, то 2 х = 128°, х = 64°,
В = 128°, то 2 х = 128°, х = 64°,  С = 180° – 128° = 52°
С = 180° – 128° = 52°
2) Если  А =
А =  В = х и
В = х и  А +
А +  С = 128°, то так как
С = 128°, то так как  А +
А +  В +
В +  С = 180°, получаем
С = 180°, получаем 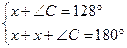 тогда
тогда 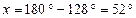 , а
, а  С = 180° – 2·52°= 76°
С = 180° – 2·52°= 76°
Ответ: 64°, 64°, 52° или 52°, 52°, 76°






