Определение. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Все точки разрыва функции делятся на точки разрыва первого и второго рода.
Определение. Точка разрыва 
называется точкой разрыва первого рода, если в этой точке существуют конечные односторонние пределы:
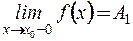и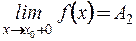 
.
При этом: а) если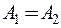 
то точка разрыва называется точкой устранимого разрыва; б) если 
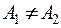, то точка разрыва называется точкой конечного разрыва.
Величину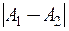 
называют скачком функции в точке разрыва первого рода.
Определение. Точка называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует или равен бесконечности.
Пример 1. Доказать, что функция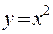 
непрерывна в точке 
.
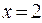¦ 1) По первому определению: 
.
2) По второму определению:
. ?
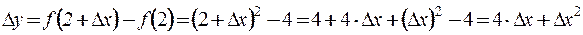
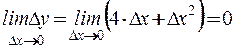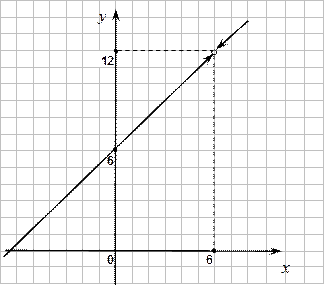
Пример 2. Исследовать функцию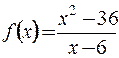 
на непрерывность.
¦ 
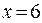– точка разрыва.
не существует, в других точках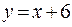 
.
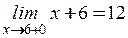
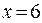– устранимый разрыв.
Функцию в точке 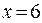можно доопределить
?
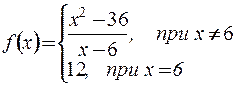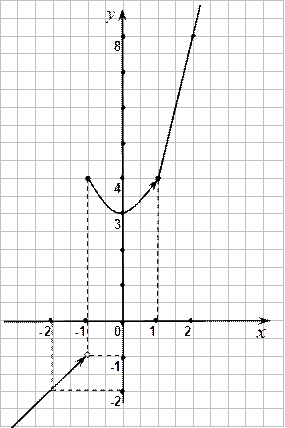
Пример 3. Найти точки разрыва функции и определить их вид.
¦ 
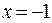
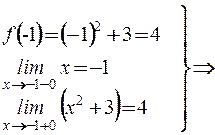
в точке 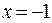разрыв первого рода.
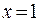
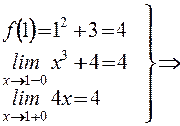
в точке 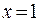функция непрерывна.
?
Пример 4. Исследовать функцию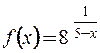 
на непрерывность
в точках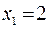 
и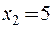 
.
¦
1) 
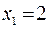
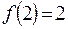
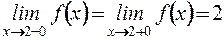– функция непрерывна.
2) 
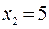
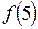не существует – следовательно, 
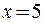- точка разрава
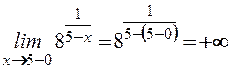
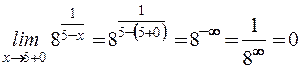
Имеем разрыв II рода.
. ?
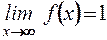Свойства функций, непрерывных на отрезке
Функции, непрерывные на замкнутом отрезке, обладают рядом свойств, которые сформулируем в виде теорем (без доказательства).
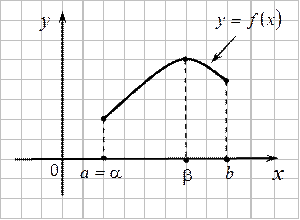Теорема 1. Если функция 
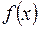непрерывна на отрезке 
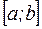, то она достигает на этом отрезке своего наибольшего и наименьшего значения, т.е. существуют точк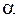и 
и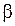 
, такие, что
, 
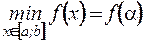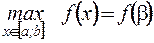. Следовательно, 
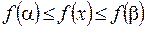для всех 
.
На рисунке 
.
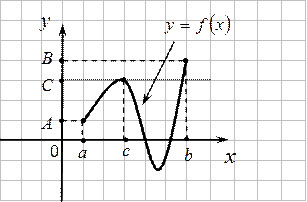
Следствие. Если функция непрерывна на отрезке, то она на нем органичена.
Теорема 2. Если функция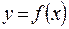 
непрерывна на отрезке 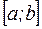и принимает на его концах неравные значения 
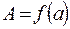и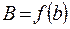 
, то на этом отрезке она принимает и все промежуточные значения между
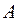и 
. Т.е. для любого числа 
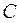, заключенного между 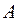и , найдется внутри этого отрезка такая точка 
, где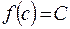 
.
Прямая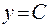 
пересечет график функции по крайней мере в одной точке.
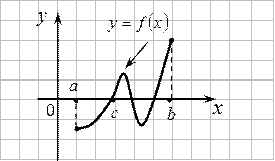Следствие. Если функция 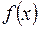непрерывна на отрезке 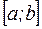и на концах отрезка принимает значения разных знаков, то на этом отрезке найдется хотя бы одна точка , в которой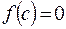 
.
Глава II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Понятие производной,
Ее геометрический и физический смысл
Определение производной
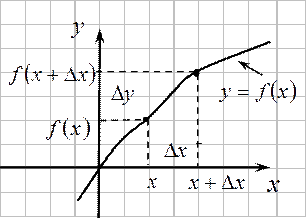
Определение. Производной от функции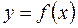 
в точке 
называется предел отношения приращения функции 
к приращению аргумента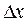 
при условии, что приращение аргумента стремится к нулю, т.е. 
.
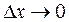Обозначение: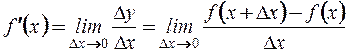 
.
Используют и другие
обозначения:
, 
, 
, 
, 
.
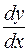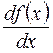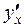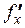Производная функции в точке 
обозначается так:
.
Функция 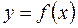, имеющая производную в каждой точке интервала 
, называется дифференцируемой на этом интервале.
Операция нахождения производной функции называется дифференцированием.
Вычислим производную функции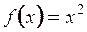 
, используя определение:
Теорема. (Связь между дифференцируемостью и непрерывностью функции).
Если функция дифференцируема в точке, то она в этой точке непрерывна. Обратное утверждение неверно.
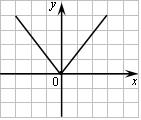Например, функция 
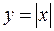в точке 
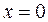непрерывна, но производная в этой точке не существует.
