Определение. Функция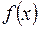 
называется бесконечно малой функцией при 
, если 
.
Аналогично определяются бесконечно малые функции при 
.
Бесконечно малые функции иначе называют бесконечно малыми величинами, или бесконечно малыми, и обозначают греческими буквами 
.
Примеры б. м. ф. функций: 
при 
;
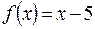при 
.
при 
.
Свойства б. м. ф.
1. Алгебраическая сумма конечного числа б. м. ф. есть б. м. ф.
2. Произведение ограниченной функции на б. м. ф. есть б. м. ф.
3. Произведение б. м. ф. на число есть б. м. ф.
4. Произведение двух б. м. ф. есть б. м. ф.
5. Частное от деления б. м. ф. на функцию, имеющую отличный от нуля предел, есть б. м. ф.
6. Частное от деления функции, имеющей отличный от нуля предел, на б. м. ф. есть б. б. ф.
7. Частное от деления функции, имеющей отличный от нуля предел, на б. б. ф. есть б. м. ф.
8. Если функция 
является б. м. ф. и не равна нулю, то функция 
есть б. б. ф. и наоборот, если функция 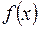является б. б. ф., то функция 
есть б. м. ф.
Примеры вычисления пределов с помощью свойств б. б. ф. и б. м. ф.
1. 
| 2. 
|
3. 
| 4. 
|
7.3. Связь между функцией, ее пределом и б. м. ф.
Теорема. Если 
, то 
,
где 
- это б. м. ф. при 
.
Доказательство.
,
т.е. 
.
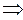
Следовательно 
это б. м. ф. при , которую обозначим через . Таким образом, 
¢.
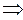
Теорема. (обратная ) Если , то
Доказательство. Так как есть б. м. ф. при , то 
.
¢
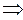
Сравнение бесконечно малых функций
Известно, что сумма, разность и произведение б. м. ф. есть б. м. ф.
Отношение б. м. ф. может быть конечным числом, или может быть б.м. ф., или может быть б. б. ф., или может вообще не стремиться ни к какому пределу.
Две б. м. ф. сравниваются между собой с помощью их отношения.
Пусть и 
являются б.м.ф. при 
.
1. Если 
, то называется б.м.ф. более высокого порядка, чем .
2. Если 
, то называется б.м.ф. более низкого порядка, чем .
3. Если 
, то и называются б. м. ф. одного порядка.
4. Если 
не существует, то и называются несравнимыми б.м.ф.
5. Если 
, то и называются эквивалентными б. м. ф.
Обозначаются эквивалентные б. м. ф. так: 
Среди б. м. ф. эквивалентные б. м. ф. играют особую роль.
Свойства эквивалентных б. м. ф.
1. Предел отношения двух б. м. ф. не изменится, если каждую или одну из них заменить эквивалентной б. м. ф.
2. Разность двух эквивалентных б.м.ф. есть б.м.ф. более высокого порядка, чем каждая из них.
3. Сумма конечного числа б.м.ф. разных порядков эквивалентна слагаемому низшего порядка.
Свойства эквивалентных б.м.ф. применяют для раскрытия неопределенностей 
при вычислении пределов.
Пример 1.
| (отбросили в числителе б. м. ф. более высокого порядка) | |
 .
| (заменили  эквивалентной ей функцией  при  ).
| |
Таблица эквивалентных б. м. ф.
1. 
| при
|
2. 
| при
|
3. 
| при
|
4. 
| при
|
5. 
| при
|
6. 
| при
|
7. 
| при
|
8. 
| при
|
9. 
| при
|
10.  ,
|  при
|
