1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению:
 ,
, 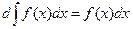 .
.
2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т.е.
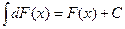 .
.
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
 .
.
4. Неопределенный интеграл от алгебраической суммы функций равен такой же алгебраической сумме неопределенных интегралов от каждой функции:
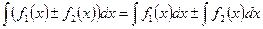 .
.
Основные формулы интегрирования (табличные интегралы).
Из каждой формулы дифференцирования вытекает соответствующая ей формула интегрирования. Например, из того, что  , следует равенство
, следует равенство  .
.
Ниже приведена таблица основных табличных интегралов:
1. 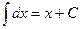
2. 
3. 
4. 
5. 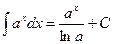
6. 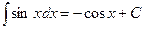
7. 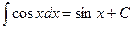
8. 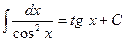
9. 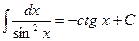
10. 
11. 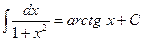
Справедливость этих формул можно проверить дифференцированием.
Непосредственное интегрирование. Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Пример 1. Найти интеграл 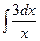 .
.
Решение. Воспользуемся определением степени с отрицательным показателем
( ) и найдем неопределенный интеграл от степени:
) и найдем неопределенный интеграл от степени:
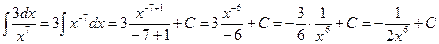 .
.
Пример 2. Найти интеграл 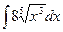 .
.
Решение. Воспользуемся определением степени с дробным показателем ( ) и найдем неопределенный интеграл от степени:
) и найдем неопределенный интеграл от степени:
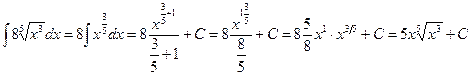 .
.
Пример 3. Найти интеграл 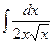 .
.
Решение. Воспользуемся определением степени с дробным показателем и правилом умножения степеней с одинаковыми основаниями (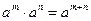 ) и найдем неопределенный интеграл от степени:
) и найдем неопределенный интеграл от степени:
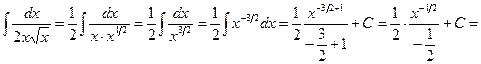
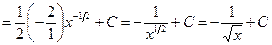
Пример 4. Найти интеграл 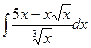 .
.
Решение. Воспользуемся определением степени с дробным показателем ( ), правилами действий над степенями с одинаковыми основаниями (
), правилами действий над степенями с одинаковыми основаниями (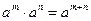 ,
, 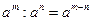 ), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеем
), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеем
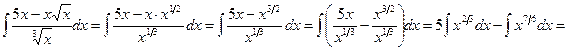

Пример 5. Найти интеграл  .
.
Решение. Раскроем скобки по формуле 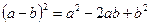 и неопределенный интеграл от полученной алгебраической суммы функций заменим такой же алгебраической суммой неопределенных интегралов от каждой функции:
и неопределенный интеграл от полученной алгебраической суммы функций заменим такой же алгебраической суммой неопределенных интегралов от каждой функции:
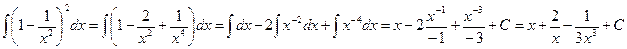 .
.
Пример 6. Найти интеграл 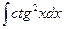 .
.
Решение. Для нахождения интеграла воспользуемся формулой 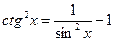 и свойствами неопределенного интеграла:
и свойствами неопределенного интеграла:
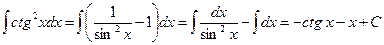 .
.
Интегрирование методом подстановки. Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки.
Сущность метода заключается в том, что путем введения новой переменной удается свести данный интеграл к новому интегралу, который сравнительно легко берется непосредственно.
Для интегрирования методом подстановки можно использовать следующую схему:
1) часть подынтегральной функции надо заменить новой переменной;
2) найти дифференциал от обеих частей замены;
3) все подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл);
4) найти полученный табличный интеграл;
5) сделать обратную замену.
Пример 7. Найти интеграл  .
.
Решение. Произведем подстановку 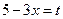 , тогда
, тогда 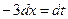 , откуда
, откуда  . Далее получаем
. Далее получаем
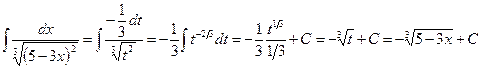 .
.
Пример 8. Найти интеграл 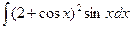 .
.
Решение. Сначала положим 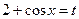 , тогда
, тогда 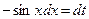 , откуда
, откуда 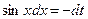 . Далее получаем
. Далее получаем

Пример 9. Найти интеграл 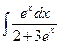 .
.
Решение. Положим 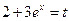 , тогда
, тогда  откуда
откуда 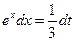 . Далее получаем
. Далее получаем
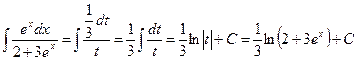 .
.
Пример 10. Найти интеграл 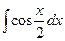 .
.
Решение. Положим 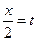 , тогда
, тогда 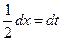 , откуда
, откуда  . Далее получаем
. Далее получаем
 .
.
В практике интегрирования часто встречаются интегралы, для нахождения которых можно использовать следующие формулы ( ,
,  - постоянные):
- постоянные):
1. 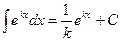
2. 
3. 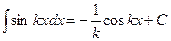
4. 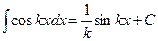
5. 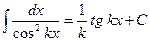
6. 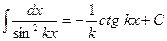
7. 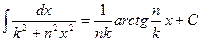
8. 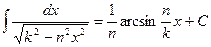
Так, при нахождении 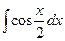 можно использовать формулу
можно использовать формулу 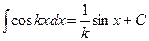 , где
, где 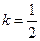 . Тогда
. Тогда 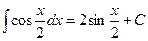 .
.
Интегрирование по частям. Здесь используют формулу: 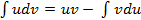
Пример 11. Найти интеграл:  Пример 12. Найдите интеграл:
Пример 12. Найдите интеграл: 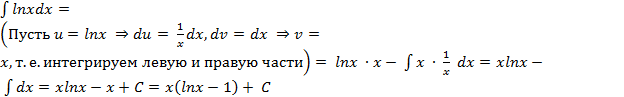 Пример 13. Найдите интеграл:
Пример 13. Найдите интеграл:
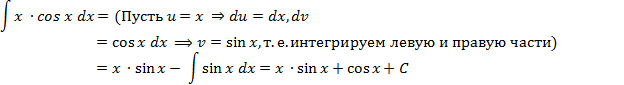
Определенный интеграл.
Понятие определенного интеграла. Пусть функция 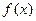 определена на отрезке
определена на отрезке 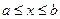 . Допустим для простоты, что функция
. Допустим для простоты, что функция 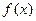 в указанном промежутке неотрицательна и
в указанном промежутке неотрицательна и 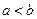 . Разобьем этот отрезок на n частей точками
. Разобьем этот отрезок на n частей точками 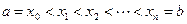 . На каждом из частичных отрезков
. На каждом из частичных отрезков 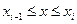 (i =1, 2, 3, …, n) возьмем произвольную точку
(i =1, 2, 3, …, n) возьмем произвольную точку  и составим сумму:
и составим сумму:
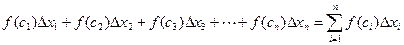 ,
,
где 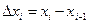 . Эта сумма носит название интегральной суммы функции
. Эта сумма носит название интегральной суммы функции 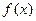 на отрезке
на отрезке 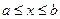 .
.
Геометрически (рис. 10) каждое слагаемое интегральной суммы равно площади прямоугольника с основанием 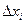 и высотой
и высотой 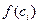 , а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.
, а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.
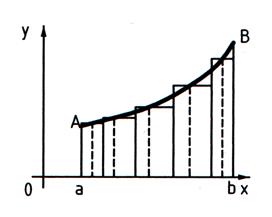
Рисунок 10
Очевидно, что при всевозможных разбиениях отрезка 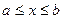 на части получим различные интегральные суммы, а, следовательно, и различные «ступенчатые фигуры».
на части получим различные интегральные суммы, а, следовательно, и различные «ступенчатые фигуры».
Будем увеличивать число точек разбиения так, чтобы длина наибольшего из отрезков 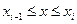 стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления
стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления 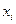 , ни от того, как выбираются точки
, ни от того, как выбираются точки  .
.
Этот предел и называется определенным интегралом от функции 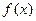 на отрезке
на отрезке 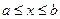 .
.
Определение 4. Определенным интегралом от функции 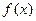 на отрезке
на отрезке 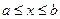 называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала. Он обозначается символом
называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала. Он обозначается символом  и читается «интеграл от a и b от функции
и читается «интеграл от a и b от функции 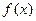 по
по  » или, короче, «интеграл от a и b от функции
» или, короче, «интеграл от a и b от функции 
 ».
».
По определению,
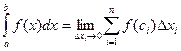 .
.
Число a называется нижним пределом интегрирования, число b – верхним; отрезок 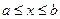 - отрезком интегрирования.
- отрезком интегрирования.
Заметим, что всякая непрерывная на отрезке 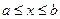 функция
функция 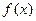 интегрируема на отрезке.
интегрируема на отрезке.
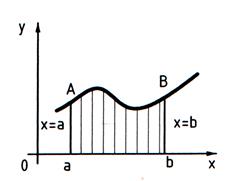
Если интегрируемая на отрезке 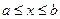 функция
функция 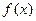 неотрицательна, то определенный интеграл
неотрицательна, то определенный интеграл  численно равен площади S криволинейной трапеции aABb, ограниченной графиком функции
численно равен площади S криволинейной трапеции aABb, ограниченной графиком функции  , осью абсцисс и прямыми
, осью абсцисс и прямыми  и
и 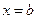 (рис. 10), т.е.
(рис. 10), т.е.  . В этом и заключается геометрический смысл определенного интеграла.
. В этом и заключается геометрический смысл определенного интеграла.
Основные свойства определенного интеграла. Все свойства сформулированы в предположении, что рассматриваемые функции интегрируемы в соответствующих промежутках.
1. Определенный интеграл с одинаковыми пределами равен нулю:
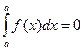
2. При перестановке пределов интегрирования знак интеграла меняется на противоположный:
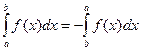 .
.
3. Отрезок интегрировании можно разбивать на части:
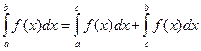 , где
, где 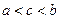
4. Постоянный множитель можно выносить за знак интеграла:

5. Интеграл от алгебраической суммы функций равен такой же алгебраической сумме интегралов от всех слагаемых:

Непосредственное вычисление определенного интеграла. Для вычисления определенного интеграла, когда можно найти соответствующий интеграл, служит формула Ньютона-Лейбница
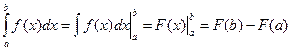 ,
,
Т.е. определенный интеграл равен разности значений любой первообразной функции при верхнем и нижнем пределах интегрирования.
Из этой формулы виден порядок вычисления определенного интеграла:
1) найти неопределенный интеграл от данной функции;
2) в полученную первообразную подставить вместо аргумента сначала верхний, затем нижний предел интеграла;
3) из результата подстановки верхнего предела вычесть результат подстановки нижнего предела.
Пример 14. Вычислить интеграл  .
.
Решение. Применив указанное правило, вычислим данный определенный интеграл:
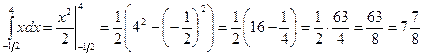
Пример 15. Вычислить интеграл 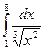 .
.
Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:
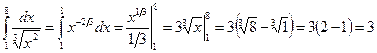
Пример 16. Вычислить интеграл 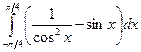 .
.
Решение. Интеграл от разности функций заменим разностью интегралов от каждой функции:

 .
.
Пример 17. Вычислить интеграл  .
.
Решение. Воспользуемся определением степени с дробным показателем, правилом деления суммы на число и вычислим определенный интеграл от каждого слагаемого отдельно:


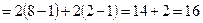
Вычисление определенного интеграла методом подстановки. Вычисление определенного интеграла методом подстановки состоит в следующем:
1) часть подынтегральной функции заменить новой переменной;
2) найти новые пределы определенного интеграла;
3) найти дифференциал от обеих частей замены;
4) все подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл);
5) вычислить полученный определенный интеграл.
Пример 18. Вычислить интеграл 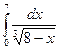 .
.
Решение. Введем подстановку 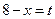 , тогда
, тогда 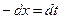 ,
,  . Определим пределы интегрирования для переменной t. При x=0 получаем
. Определим пределы интегрирования для переменной t. При x=0 получаем 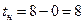 , при x=7 получаем
, при x=7 получаем  .
.
Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
 .
.
Пример 19. Вычислить интеграл  .
.
Решение. Произведем подстановку 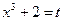 , тогда
, тогда 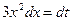 ,
, 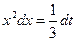 . Определим пределы интегрирования для переменной t. При x=1 получаем
. Определим пределы интегрирования для переменной t. При x=1 получаем  , при x=2 получаем
, при x=2 получаем  .
.
Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
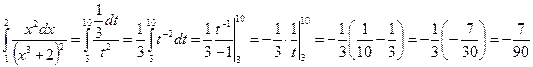 .
.
Пример 20. Вычислить интеграл 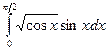 .
.
Решение. Положим 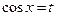 , тогда
, тогда 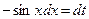 и
и 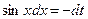 . Определим пределы интегрирования для переменной t:
. Определим пределы интегрирования для переменной t: 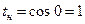 ,
, 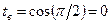 .
.
Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим


Пример 21. Вычислить интеграл 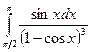 .
.
Решение. Пусть 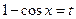 ,
,  ,
,  ,
, 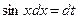 .
.

Пример 22. Вычислить интеграл 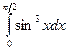 .
.
Решение. Сначала преобразуем подынтегральное выражение:
 .
.
Затем вычислим интеграл от разности функций, заменив его разностью определенных интегралов от каждой функции:
 .
.
Вычислим каждый интеграл отдельно:
 ;
;
Пусть 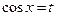 ,
, 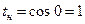 ,
, 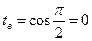 ,
, 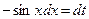 ,
, 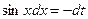 .
.
 .
.
Тогда
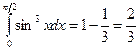
Интегрирование по частям. Здесь используют формулу: 
Пример 23. Вычислите интеграл: 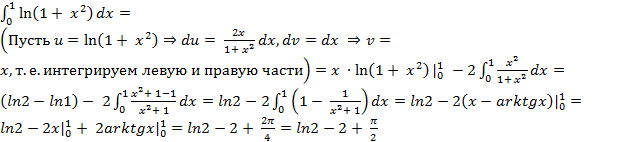
Пример 24. Вычислите интеграл:
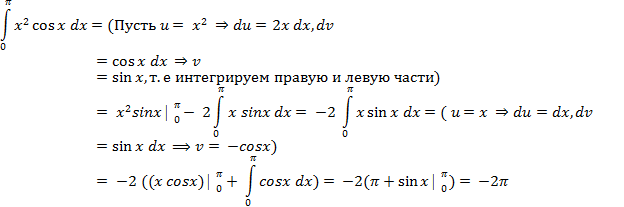
Приложение определенного интеграла.
Понятие определенного интеграла широко применяется для вычисления различных геометрических и физических величин.
Площади плоских фигур.
1. Фигура ограниченная графиком непрерывной и неотрицательной на отрезке [a;b] функции f(x), осью Ох и прямыми х = а, х = b. Площадь данной фигуры находится по S = 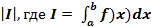 (1)
(1)
Пример 25: Вычислить площадь фигуры ограниченной линиями  . Решение: Построим графики данных функций: а)
. Решение: Построим графики данных функций: а) 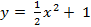 - кв. ф., график – парабола, ветви направленны вверх. Вершина находится в точке с координатами (0; 1).
- кв. ф., график – парабола, ветви направленны вверх. Вершина находится в точке с координатами (0; 1).
Находим доп. точки, для этого строим таблицу:

| Х | ±1 | ±2 | ±3 |
| у | 1,5 |   5,5 5,5
|
 б) у = 0 – ось Ох
б) у = 0 – ось Ох
в) х = - 2, х = 3 – прямые, У у = 
 параллельные оси Оу
параллельные оси Оу
 |












 Х = - 2 1 х = 3
Х = - 2 1 х = 3




 0 Х
0 Х
- 2 1 3
S = 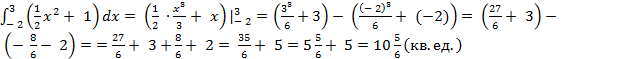
Пример 26: Вычислить площадь фигуры ограниченной линиями y = - x2 – 1, y = 0, x = - 1, x = 2.
Решение: Построим графики данных функций: а) у = - х2 – 1 – квадратичная функция, графиком является парабола, ветви направлены вниз. Вершина находится в точке с координатами (0; - 1). Находим доп. точки, для этого строим таблицу:
| Х | ±1 | ± 2 | ± 3 |
| У | - 2 | - 5 | - 10 |
б) у = 0 – ось Ох; х = - 1, х = 2 – прямые параллельные оси Оу
 У
У





 0 Х
0 Х

















 - 2 - 1 1 2 3
- 2 - 1 1 2 3
Х = -1 Х = 2
У = - х2 – 1
I = 
S = 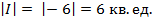
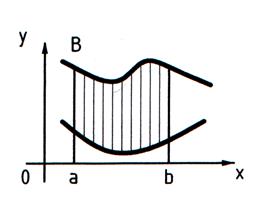
2. Фигура, ограниченная графиками двух непрерывных на отрезке [a; b] функций f(x) и g(x) и прямыми x = a, x = b, где f(x) ≥ g(x). В этом случае искомая площадь вычисляется по формуле
S =  (2)
(2)

Пример 27: Вычислить площадь фигуры ограниченной линиями 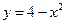 ,
, 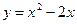 .
.
Решение:1) Найдем пределы интегрирования, т.е. абсциссы точек пересечения графиков функций 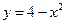 и
и 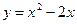 . Для этого решим систему
. Для этого решим систему

Имеем 
 ,
,  , a = 1, b= - 1, c = - 2
, a = 1, b= - 1, c = - 2
D = 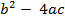
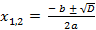
D = (- 1)2 - 4· 1· (- 2) =9 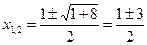 ,
, 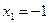 ,
, 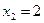 .
.
Следовательно a = - 1, b = 2
2)Построим графики функций:
а) y = 4 – x2 - квадратичная функция, график – парабола, ветви вниз. Вершина находится в точке с координатами (0;4). Находим доп. точки, для этого строим таблицу:
| Х | ±1 | ± 2 | ± 3 |
| У | - 5 |
б) y = x2 - 2x – квадратичная функция, график – парабола, ветви направлены вверх. Найдем координаты вершины параболы: хв = - 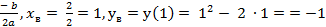 .
.
Вершина находится в точке с координатами (1; - 1). Находим доп. точки, для этого строим таблицу:

 У
У
| Х | - 1 | ||
| У | 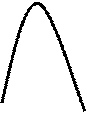  0 0
|
 у = х2 – 2х
у = х2 – 2х
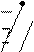 | |||
 | |||

 0
0 












 У = 4 – х2
У = 4 – х2
Искомую площадь вычисляем по формуле (2):
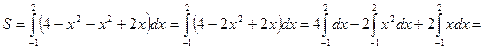
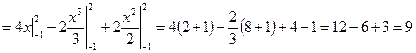 ;
; 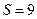 кв. ед.
кв. ед.















 3.Фигура, ограничена осью Ох, прямыми x = a, x = b и графиком функции f(x), которая непрерывна на данном отрезке и меняет свой знак конечное число раз на этом отрезке. В этом случае отрезок [a;b] разбивают на части. Искомая площадь Sчисленно равна алгебраической сумме интегралов, взятых по каждому из полученных отрезков, т. е.
3.Фигура, ограничена осью Ох, прямыми x = a, x = b и графиком функции f(x), которая непрерывна на данном отрезке и меняет свой знак конечное число раз на этом отрезке. В этом случае отрезок [a;b] разбивают на части. Искомая площадь Sчисленно равна алгебраической сумме интегралов, взятых по каждому из полученных отрезков, т. е.
S = S1 + S2, S1 = 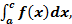 S2 =
S2 = 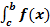 dx
dx
У
S1
X
а c S2 b


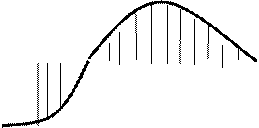
 Пример 28: Вычислите площадь фигуры, ограниченной линиями y = sinx, x = -
Пример 28: Вычислите площадь фигуры, ограниченной линиями y = sinx, x = -  , x=
, x= 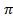 . Решение: Построим графики функций: У
. Решение: Построим графики функций: У
 1
1
 |
х = -  0 π Х
0 π Х
 0
0
S = S1 + S2; S1 = 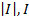 =
= 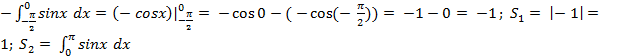 = (- cos x)
= (- cos x)  =2; S = 1 + 2 = 3 кв. ед.
=2; S = 1 + 2 = 3 кв. ед.
4.Фигура ограничена графиками трех и более непрерывных на отрезка [a;b] функций. В этом случае искомую площадь вычисляют как алгебраическую сумму площадей, вычисление каждой из которых сводится к одному из предыдущих случаев.
Пример 29: Вычислите площадь фигуры, ограниченной линиями y = 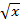 ; y =
; y =  ; y = 2x. Решение: 1) Находим пределы интегрирования, т.е. точки пересечения графиков функций. Для этого необходимо решить 3 системы уравнений:
; y = 2x. Решение: 1) Находим пределы интегрирования, т.е. точки пересечения графиков функций. Для этого необходимо решить 3 системы уравнений:
а) 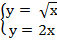
Имеем  , возведем обе части уравнения в квадрат
, возведем обе части уравнения в квадрат
х = 4х2
4х2 – х = 0
х(4х – 1) = 0
х1 = 0 или 4х – 1 = 0
4х = 1
х2 = 
б)  Имеем
Имеем 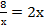
8 = 2х2
х2 = 4
х1,2 = ± 2
в) 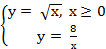 Имеем
Имеем 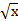 =
= 
х = 
х3 = 64
х = 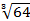 = 4
= 4
2) Построим графики данных функций:
а) у = 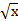 - графиком является ветвь параболы, расположенная в 1 четверти, т. к. х ≥ 0.
- графиком является ветвь параболы, расположенная в 1 четверти, т. к. х ≥ 0.
| Х | ||||
| у |
б) y =  - обратная пропорциональность, графиком является гипербола, расположенная в I и в III координатных четвертях.
- обратная пропорциональность, графиком является гипербола, расположенная в I и в III координатных четвертях.
| Х | ± 1 | ± 2 | ± 4 | ± 8 |
| У | ± 8 | ± 4 | ± 2 | ± 1 |
в) у = 2х – прямая пропорциональность, графиком является прямая, проходящая через начала координат.
| Х | ||
| У |
Т. К. х ≥ 0, то графики достаточно построить в 1 координатной четверти
 У
У 




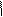



 у =
у = 
 |
у = 2х


 |


 У =
У = 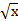







 2
2
3) Находим площадь фигуры. Она равна сумме площадей на отрезке [ 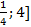 , т. е.
, т. е.
S = S1 + S2, где S1 = 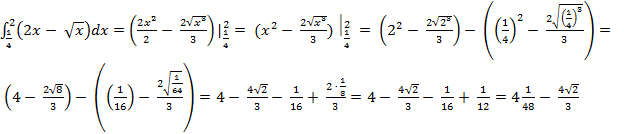 (кв. ед.)
(кв. ед.)
S2 = 
S = 
Дифференциальные уравнения.
Понятие о дифференциальном уравнении.
Определение 1. Дифференциальным уравнением называется уравнение, связывающее независимую переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции).
Определение 2. Если дифференциальное уравнение содержит производную или дифференциал не выше первого порядка, то оно называется дифференциальным уравнением первого порядка. Общий вид такого уравнения 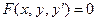 , где
, где 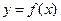 - искомая функция,
- искомая функция, 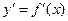 - ее производная по x, а F – заданная функция переменных x, y, y’.
- ее производная по x, а F – заданная функция переменных x, y, y’.
Определение 3. Общим решением дифференциального уравнения первого порядка называется функция  от x и произвольной постоянной C, обращающая это уравнение в тождество по x.
от x и произвольной постоянной C, обращающая это уравнение в тождество по x.
Общее решение, записанное в неявном виде 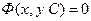 , называется общим интегралом.
, называется общим интегралом.
Определение 4. Частным решением уравнения 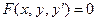 называется решение, полученное из общего решения при фиксированном значении C:
называется решение, полученное из общего решения при фиксированном значении C: 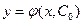 , где
, где 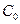 - фиксированное число.
- фиксированное число.
Определение 5. Частным интегралом уравнения 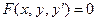 называется интеграл, полученный из общего интеграла при фиксированном значении C:
называется интеграл, полученный из общего интеграла при фиксированном значении C: 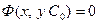 .
.
Определение 6. График любого частного решения дифференциального уравнения 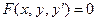 называется дифференциальной кривой. Общему решению (и общему интегралу) этого уравнения соответствует семейство интегральных кривых, зависящих от одного параметра.
называется дифференциальной кривой. Общему решению (и общему интегралу) этого уравнения соответствует семейство интегральных кривых, зависящих от одного параметра.
Определение 7. Задача нахождения частного интеграла дифференциального уравнения n -го порядка (n =1, 2, 3, …), удовлетворяющего начальным условиям вида  ,
, 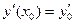 ,
,  , …,
, …, 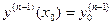 , называется задачей Коши.
, называется задачей Коши.
Задача Коши для дифференциального уравнения первого порядка состоит в том, чтобы найти решение, удовлетворяющее начальному условию  . Другими словами, из всех интегральных кривых данного дифференциального уравнения требуется выделить ту, которая проходит через точку
. Другими словами, из всех интегральных кривых данного дифференциального уравнения требуется выделить ту, которая проходит через точку  .
.
Пример 1. Составить уравнение кривой 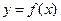 , если угловой коэффициент касательной, проведенной в любой точке кривой равен 2 x.
, если угловой коэффициент касательной, проведенной в любой точке кривой равен 2 x.
Решение. Так как на основании геометрического смысла производной  , то получим дифференциальное уравнение первого порядка:
, то получим дифференциальное уравнение первого порядка:
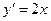 ,
, 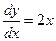 ,
, 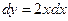 .
.
Чтобы найти искомую функцию 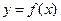 , надо проинтегрировать обе части уравнения
, надо проинтегрировать обе части уравнения 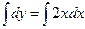 . Отсюда получим общее решение дифференциального уравнения:
. Отсюда получим общее решение дифференциального уравнения: 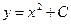 . Геометрически это решение представляет собой семейство парабол с вершиной на оси Oy, симметричных относительно этой оси (рис. 18).
. Геометрически это решение представляет собой семейство парабол с вершиной на оси Oy, симметричных относительно этой оси (рис. 18).
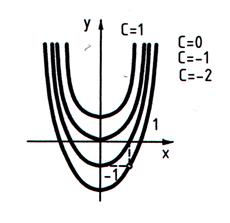
Рисунок 18.
Чтобы из общего решения выделить частное решение, надо задать начальные условия. Пусть 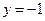 при
при 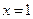 , тогда общее решение примет вид
, тогда общее решение примет вид  , откуда
, откуда 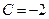 . Геометрически частное решение
. Геометрически частное решение 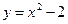 представляет собой параболу, проходящую через точку (1, -1) (рис. 68).
представляет собой параболу, проходящую через точку (1, -1) (рис. 68).
Дифференциальные уравнения с разделяющимися переменными. Общий вид такого уравнения

где 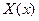 ,
,  - функции только от x,
- функции только от x, 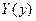 ,
, 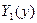 - функции только от y.
- функции только от y.
Поделив обе части уравнения на произведение 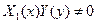 , получим уравнение с разделяющимися переменными:
, получим уравнение с разделяющимися переменными:
 .
.
Общий интеграл этого уравнения имеет вид
 .
.
Замечание. Если произведение 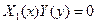 при x=a и y=b, то эти функции x=a и y=b являются решениями дифференциального уравнения при условии, что при этих значениях x и y уравнение не теряет числового смысла. Геометрически эти решения представляют собой прямые, параллельные осям координат.
при x=a и y=b, то эти функции x=a и y=b являются решениями дифференциального уравнения при условии, что при этих значениях x и y уравнение не теряет числового смысла. Геометрически эти решения представляют собой прямые, параллельные осям координат.
Пример 2. Решить уравнение 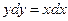 . Найти частное решение, удовлетворяющее условию y =4 при x = - 2.
. Найти частное решение, удовлетворяющее условию y =4 при x = - 2.
Решение. Это уравнение с разделенными переменными. Интегрируя, находим общее решение уравнения:
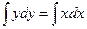 ,
, 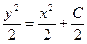 .
.
Для получения более простого по форме общего решения постоянное слагаемое в правой части представлено в виде C/2. Тогда
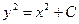 .
.
Подставив в общее решение значения y =4 и x = - 2, получим 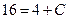 , откуда
, откуда 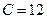 .
.
Пример 3. Найти общий интеграл дифференциального уравнения 
Решение. Так как  , то
, то
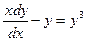 , откуда
, откуда  .
.
Разделим обе части уравнения на произведение 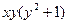 :
:
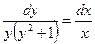 .
.
Преобразуем дробь:
 .
.
Тогда
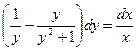 .
.
Интегрируя, находим
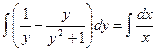 ,
, 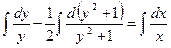 ,
,  .
.
Для облегчения потенцирования и получения более простого по форме общего решения постоянное слагаемое в правой части представлено в виде 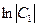 . После потенцирования получим
. После потенцирования получим
 , откуда
, откуда  , или
, или  , где
, где 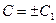 .
.
Произведение  при
при 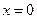 и
и  . При этих значениях x и y дифференциальное уравнение не теряет числового смысла, поэтому
. При этих значениях x и y дифференциальное уравнение не теряет числового смысла, поэтому 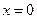 и
и  - решение уравнения, но решение
- решение уравнения, но решение  входит в решение
входит в решение  при
при  .
.
Значит, решения уравнения имеют вид 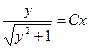 и
и 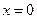 .
.
Пример 4. Решить уравнение  . Найти частное решение, удовлетворяющее условию
. Найти частное решение, удовлетворяющее условию 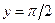 при
при 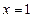 .
.
Решение. Разделим каждый член уравнения на произведение 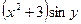 :
:
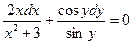 .
.
Интегрируя, находим
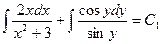 ,
, 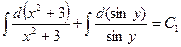 ,
,  .
.
После потенцирования получим  ,
, 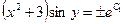 или
или 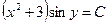 , где
, где 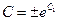 . Отсюда
. Отсюда 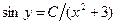 .
.
Произведение  при
при 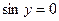 ; так как при этом значени
; так как при этом значени






