Определение 8. Кривая у = f(x) называется выпуклой вниз на промежутке а < х <в, если она лежит выше касательной в любой точке этого промежутка и кривая у = f(x) называется выпуклой вверх на промежутке а < х <в, если она лежит ниже касательной в любой точке этого промежутка.
Определение 9. Промежутки, в которых график функции обращён выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Y
 |
Y = f(x)
 |
0 X
Достаточное условие выпуклости кривой. График дифференцируемой функции Y = f(x) является выпуклым вверх на промежутке а < х <в, если f”(x) < 0 и выпуклым вниз, если f”(x) > 0.
Определение 9. Точки, в которых вторая производная равна нулю или не существует, называются критическими точками II рода.
Определение 10. Точка графика функцииY = f(x), разделяющая промежутки выпуклости противоположенных направлений этого графика, называется точкой перегиб.
+ - f”(x)
 |
х = х0 f(x)
точка перегиба
Пример 16: Дана функция у = х3 – 2х2 + 6х – 4.Исследовать функцию на промежутки монотонности и точки экстремума. Определить направление выпуклости и точки перегиба.
Решение: 1. Найдем область определения функции: D(y) = 
;
2. Найдем первую производную: y’ = 3x2 – 4x + 6;
3. Решим уравнение: y’ = 0, 3x2 – 4x + 6 = 0, D 
0, то данное уравнение не имеет решения, следовательно точек экстремуму нет. y’ 
, то функция возрастает на всей области определения.
4. Найдем вторую производную:y” = 6x – 4;
5. Решим уравнение: y” = 0, 6x – 4 = 0, х = 
- + y”(x)
y(x)
У() = - 
Ответ: (; - ) – точка перегиба, функция выпукла вверх при х 
и выпукла вверх при х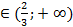 
Асимптоты.
Определение 11.:Асимптотой кривой называется прямая, к которой неограниченно приближается график данной функции.
Виды асимптот:
1) Вертикальные асимптоты. График функции y = f(x) имеет вертикальную асимптоту, если 
. Уравнение вертикальной асимптоты имеет вид х = а
2) Горизонтальные асимптоты. График функции y = f(x) имеет горизонтальную асимптоту, если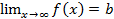 
. Уравнение горизонтальной асимптоты имеет вид у = b.
Пример 17: Для функция y = 
найдите асимптоты.
3) Наклонные асимптолты. Прямая y = kx + b называется наклонной асимптотой графика функции y = f(x), если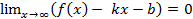 
. Значения k и b вычисляются по формулам: k = 
; b = 
.
Решение: 
, то y = 0 – горизонтальная асимптота;
(т. к. х – 3 ≠ 0, х ≠3), то х = 3 – вертикальная асимптота. 
,т. е. k = 0, то кривая наклонной асимптоты не имеет.
Пример 18: Для функции y =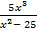 
найдите асимптоты.
Решение: x2 – 25 ≠ 0 при x ≠ ± 5, то х = 5 и х = - 5 являются горизонтальными асимптотами;
y = 
, то кривая не имеет вертикальной асимптоты;
k = 
; b = 
, т. е. y = 5x – наклонная асимптота.
Примеры построения графиков функций.
Пример 19.
Исследовать функцию и построить график функции у = х3 – 6х2 + 9х – 3
1.Найдём область определения функции: D(y) = R
2.Выясним, является ли данная функция чётной или нечетной:
у(- х) = (- х)3 - 6·(- х)2 + 9·(-х) – 3 = - х3 – 6х2 – 9х – 3 = - (х3 + 6х2 + 9х + 3), т. е.
у(- х) ≠ у(х) – не является чётной и у(- х) ≠ - у(х) – не является нечётной
(у = х5 – х3 – нечетная, у = х4 + х2 – четная)
3.Не является периодической.
4.Найдем точки пересечения с осями координат: если х = 0, то у = - 3 (0; - 3)
если У = 0, х найти затруднительно.
5.Найдем асимптоты графика функции: Вертикальных асимптот нет, т.к. нет значений х, при которых функция неопределенна; у = 
, т. е. горизонтальных асимптот нет;
k = 
, т. е. наклонных асимптот нет.
6.Исследуем функцию на промежутки монотонности и её экстремумы: y’ = 3x2 – 12x + 9, y’= 0, 3x2 – 12x + 9 = 0 
x1 = 1; x2 = 3 – критические точки 1 рода.
+ - + y’(x)
x
1 3 y(x)
max min
ymax = y(1) = 1, (1;1) – точка максимума; ymin = y(3) = - 3, (3; - 3) – точка минимума, функция у↑ при х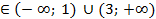 
и у 
.
7.Исследуем функцию на промежутки выпуклости и точки перегиба: y” = (y’)’ = (3x2 – 12x + 9)’ = 6x – 12, y” = 0, 6x – 12 = 0 x = 2
- + y”(x)
x
2 y(x)
Y(2) = - 1 (2; - 1) – точка перегиба, функция выпукла вверх при х 
и выпукла вниз при х 
.
8.Дополнительные точки:
| х | - 1 | |
| у | - 19 |
9. Построим график функции:
У
 |
1
0 1 2 3 4 Х
- 3
- 19
Пример 20.
Исследовать функцию и построить график функции у = 
1. Найдём область определения функции: 1 – х ≠ 0, х ≠ 1, D(y) = 
.
2.Выясним, является ли данная функция чётной или нечетной: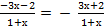 
,
у(- х) ≠ у(х) – не является чётной и у(- х) ≠ - у(х) – не является нечётной
3.Не является периодической.
4.Найдем точки пересечения с осями координат: х = 0, то у = - 2; у = 0, 
, то 
, т. е. (0; - 2); (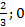
).
5.Найдем асимптоты графика функции: т.к. х ≠ 1,то прямая х = 1 – вертикальная асимптота;
у = 
, т. е. у = - 3 - горизонтальная асимптота;
k = 
, т. е. наклонных асимптот нет.
6.Исследуем функцию на промежутки монотонности и её экстремумы: y’ = 
= 
, y’ ≠ 0, т. е. критических точек 1 рода нет, но у’ > 0, то функция возрастает на всей области определения.
7.Исследуем функцию на промежутки выпуклости и точки перегиба:
y” = (y’)’ = (
, x ≠ 1
+ - f” (x)
x
1 f(x)
т. к. х = 1 
D(y), то не является точкой перегибах х = 1 – точка разрыва, функция выпукла вниз при х 
и выпукла вверх при х 
8. Дополнительные точки:
| х |  - 1
| ||
| у | - 2,5 | - 4 | - 3,5 |
9.Построим график функции:
У
Х = 1
- 1 0 1 2 3 Х
- 2
У = -3
- 3
- 4
Пример 21:
Исследовать функцию и построить график функции у = 
1. Найдём область определения функции: х ≠ 0, D (y) = (- ∞; 0) U (0; + ∞)
2. Выясним, является ли данная функция чётной или нечетной: y(- x) = - , y(x) = - y(x) – то функция нечётная и график симметричен относительно начала координат.
3. Не является периодической.
4. Найдем точки пересечения с осями координат: х ≠ 0, то у ≠ 0, график не пересекает ось оУ; 3х2+ 1 = 0, х2 = - 
- нет решения, то график не пересекает ось оХ
5. Найдем асимптоты графика функции: т.к. х ≠ 0,то прямая х = 0 – вертикальная асимптота;
у = 
, т. е. горизонтальных асимптот нет;
k = 
, т. е.y = 3x - наклонная асимптота.
6. Исследуем функцию на промежутки монотонности и её экстремумы:
y’ = 
, y’ = 0,
= 0, 3x2 – 1 = 0, x = ± 
= 
- критические точки 1 рода.
+ - + y’(x)
X
Y(x)
max min
y(-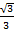 
) = 
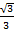y() = 2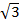 
(
) – точка минимума; (
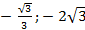) – точка максимума; У ↑ при Х 
; y 
7.Исследуем функцию на промежутки выпуклости и точки перегиба: y” = (y’)’ = 
; x ≠ 0;
- 
+ y”(x)
- 
X
0 Y(x)
т. к. х = 0 D(y), то не является точкой перегиба,х = 0- точка разрыва; функция выпукла вверх при х 
и выпукла вниз при
х 
Дополнительные точки:
| х | - 1 | - 0,5 | - 0,1 | 0,1 | 0,5 | |
| у | - 4 | - 3,5 | - 10,3 | 3,5 |
8.Построим график функции: У
У = 3х
 |
3
 |
1
0 Х
- 1 - 0,5 - 0,1 0,1 0,5 1
Упражнения для самопроверки
1. Найдите производные функций: а) 
; б)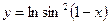 
;
2. Найдите вторую производную функции: а) 
; б) 
; в) 
.
3. Составьте уравнение касательной к кривой 
в начале координат.
4. При каком значении переменной x касательные к кривым 
и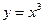 
параллельны?
5. Тело движется прямолинейно по закону 
(
- в метрах,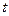 
- в секундах). Найдите скорость движения в тот момент времени, когда ускорение равно нулю.
6. Найдите экстремумы функции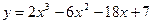 
.
7. Найдите наибольшее и наименьшее значения функции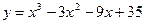 
на отрезке 
.
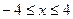8. Кусок проволоки длиной в 84 см требуется согнуть в виде прямоугольника так, чтобы площадь этого прямоугольника была наибольшей.
9. Число 16 разложите на два таких положительных множителя, чтобы сумма их квадратов была наименьшей.
10. Определите направление вогнутости и точки перегиба кривой 
.
Ответы. 1 а) 
; б) 
; 2. а) 
; б) 
; в) 
. 3. 
. 4. 0; 
. 5. 
м/с. 6. 
, 
. 7.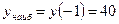 
, 
. 8. Квадрат со стороной 21 см. 9. 4 и 4. 10. На интервале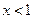 
кривая выпукла, на интервале 
- вогнута, точка перегиба (1, 2).
Интегральное исчисление.
По данной теме ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки.
Неопределенный интеграл
Понятие неопределенного интеграла. Напомним, что дифференцирование – это действие, с помощью которого по данной функции находится ее производная или дифференциал. Например, если 
, то 
, 
.
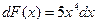Как мы знаем, нахождение производной имеет большое практическое значение. Так, по данному закону движения тела 
мы путем дифференцирования находим скорость 
, а затем и ускорение 
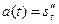по данному уравнению кривой 
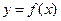определяем угловой коэффициент касательной, проведенной к этой кривой: 
.
На деле, однако, часто приходится решать обратную задачу: по известной скорости движения тела устанавливать закон его движения, по данному угловому коэффициенту касательной к кривой находить уравнение кривой и т.п. иначе говоря, по данной производной отыскивать функцию, от которой найдена эта производная, т.е. выполнять действие обратное дифференцированию. Это действие называется интегрированием. С помощью интегрирования по данной производной или дифференциалу функции находится сама функция. Например, если 
, то 
, так как 
.
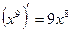Определение 1. Дифференцируемая функция 
, 
называется первообразной для функции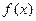 
на интервале , если 
для каждого .
Так, для функции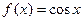 
первообразной служит функция 
, поскольку 
.
Для заданной функции ее первообразная определяется неоднозначно.
Справедливо теорема: если - первообразная для 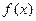на некотором промежутке, то и функция 
, где C – любая постоянная, также является первообразной для функции 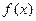на этом промежутке. Обратно: каждая функция, являющаяся первообразной для 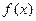в данном промежутке, может быть записана в виде .
Значит, достаточно найти для данной функции 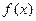только одну первообразную функцию , чтобы знать все первообразные, так как они отличаются друг от друга только на постоянную величину.
Определение 2. Совокупность всех первообразных функций 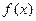на интервале называют неопределенным интегралом от функции 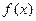на этом интервале и пишут 
. Здесь 
- подынтегральное выражение; 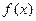- подынтегральная функция; x – переменная интегрирования; C – произвольная постоянная.
Например, 
, так как 
.
Определение 3. Если функция 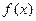имеет на некотором промежутке хотя бы одну первообразную, то ее называют интегрируемой на этом промежутке. Можно доказать, что любая функция, непрерывная на отрезке 
, интегрируема на этом отрезке.
