Комплексное число z = a + bi можно изобразить на координатной плоскости точкой М(х;у), при этом действительные числа изображаются точками на оси абсцисс, которую называют действительной осью, а мнимые числа – точками оси ординат, которую называют мнимой осью. А также, произвольную точку М плоскости, не совпадающую с точкой О, можно задать двумя числами: r – длина отрезка ОМ и φ – углом, который образует отрезок ОМ с осью ОР в положительном направлении. Числа r и φ называются полярными координатами точки М. Совокупность точки О и оси ОР образуют полярную систему координат. О называется полюсом, а ОР – полярной осью.
Полярные координаты точек плоскости изменяются в следующих пределах:
0 
У
у М(х;у)
r
φ
О х Р
Пусть на плоскости выбраны одновременно полярные и прямоугольные системы координат, то х = r 
y = r 
(4), где r = 
= 
(5) - называется модулем или абсолютной величиной комплексного числа и обозначается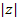 
, а φ – аргументом комплексного числа и обозначается arg z (0 
arg z <2π).
tgφ = 
(6)
Определение 4: Комплексное число z = χ + iy = r( 
называется тригонометрической формой комплексного числа.
Для числа z = 0 аргумент не определён.
Любое комплексное число z ≠ 0 имеет бесконечно много аргументов, отличающихся друг от друга на число, кратное 2π.
Определение 5: Наименьшее по абсолютной величинезначение аргумента из промежутка – π < φ ≤ π называется главным значением аргумента.
Пример 8: Найдите модуль и главное значение аргумента комплексного числа z = - 5i.
Решение: z = - 5i = 0 – 5i, т.е. х = 0, у = - 5, то М(0;- 5), следовательно М находится на отрицательной полуоси Оу, значит φ = - 
. Используя формулу (5) найдем значение модуля = 
= 5.
Пример 9: Найдите все значения аргумента комплексного числа z = 1 – i.
Решение: х = 1, у = - 1. Используя формулу (6), находим tgφ = - 1, значит φ = - 
+ 2πк, к 
Z.
Действия над комплексными числами, заданными в тригонометрической форме.
1) Правило умножения: При умножении двух комплексных чисел, заданных в тригонометрической форме, их модули умножаются, а аргументы складываются, т. е. z1 = r1(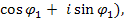 
z1 = r2( 
z1z2 = r1r2( 
). (7)
Пример 9: Дано z1 = 2(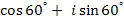
); z2 = 3(
).
Найдите z1z2.Решение: Используя формулу (7), получим
z1z2 = 2* 3(
= 6(
) = - 1
2) Правило деления: При делении двух комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются, т. е.. z1 = r1( 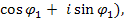z1 = r2(
(8)
Пример 10: Дано z1 = 3(
); z2 = 2(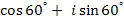). Вычислить 
.
Решение: Используя формулу (8), получим = 
= 1,5(
+ i 
) = 1.5(
)) = 
- 
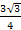i) = 
- 
i
3) Правило: При возведении комплексного числа в степень n модуль этого числа возводится в степень n, а аргумент умножается на n, т. е.
(9)
r = 1, то 
= 
– формула Муавра (10)
Пример 11: Возведите в 6 –ю степень комплексное число 
.
Решение: Используя формулу (10), получим
= 
