Контрольная работа № 1
В результате проведения эксперимента получены результаты наблюдений при различных уровнях фактора. Необходимо обработать результаты наблюдений, используя методику дисперсионного анализа (ДА), чтобы подтвердить или отклонить нулевую гипотезу Н 0.
ДА удобен тем, что он позволяет оценивать влияние неизмеряемых качественных факторов на количественные показатели. Например, влияние той или иной технологии на качество продукции и т.д.
Перед выполнением работы необходимо сформулировать гипотезу, если она не указана в задании, и установить по таблице задания, где расположены уровни фактора А и результаты наблюдений, для того чтобы их правильно занести в расчетную таблицу 1.
Основное уравнение дисперсионного анализа представляет собой разложение суммы квадратов отклонений результатов наблюдений от общего среднего на сумму квадратов отклонений средних по уровню от общего среднего и сумму квадратов отклонений внутри испытаний (правило разложения вариации).
 .
.
Суммы квадратов отклонений, делённые на соответствующее число степеней свободы f, являются несмещенными оценками дисперсий:
общей —  факторной —
факторной — 
ошибки — 
где f общ =N – 1; f А = k – 1; f ош = N – k;
 — общее число наблюдений;
— общее число наблюдений;
nj — число наблюдений на j -м уровне;
k — число уровней фактора.
Если по всем уровням фактора одинаковое число наблюдений n, то N=k× n.
Заключительным этапом дисперсионного анализа является сравнение двух дисперсий 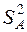 и
и  с помощью F -критерия Фишера
с помощью F -критерия Фишера

Расчетное значение F -критерия сравнивается с его табличным значением, найденным по заданному уровню значимости α или доверительной вероятности (надежности вывода) p= 1 – α и соответствующему числу степеней свободы fA и f ош:  . Значения α выбираются обычно из ряда 0,01, 0,05, 0,10.
. Значения α выбираются обычно из ряда 0,01, 0,05, 0,10.
Если F расч ³ F крит, то гипотеза Н 0, заключающаяся в том, что различие между сравниваемыми величинами  и
и  отсутствует, отвергается. Это значит, что различие между дисперсиями
отсутствует, отвергается. Это значит, что различие между дисперсиями  и
и  существенно и изучаемый фактор влияет на признак качества (исследуемый фактор y), т.е. влияние фактора значимо. Если F расч < F крит, то в этом случае нулевая гипотеза принимается: различие между сравниваемыми дисперсиями случайное и фактор не влияет на выходной параметр.
существенно и изучаемый фактор влияет на признак качества (исследуемый фактор y), т.е. влияние фактора значимо. Если F расч < F крит, то в этом случае нулевая гипотеза принимается: различие между сравниваемыми дисперсиями случайное и фактор не влияет на выходной параметр.
Табличные значения F -критерия больше единицы, поэтому числитель должен быть больше знаменателя, т.е. если  <
<  , то они меняются местами.
, то они меняются местами.
На практике обычно используют следующие формулы для нахождения сумм квадратов:
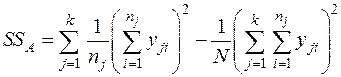 — различие между уровнями;
— различие между уровнями;
 — различие внутри уровней.
— различие внутри уровней.
Если количество наблюдений на каждом уровне одинаковое (nj = n), то 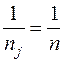 выносятся перед суммой
выносятся перед суммой 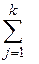 .
.
Для выполнения дисперсионного анализа результаты наблюдений и промежуточных расчетов удобнее сводить в таблицу 1.
Таблица 1 — Опытные и расчетные данные
| Уровень фактора | Результаты наблюдений | Сумма по уровню | Квадрат суммы по уровню | Сумма квадратов наблюдений по уровню | ||||
| … | i | … | nj | |||||

| … |

| … |

| 
| 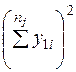
| 
| |
| … | ||||||||
| j | 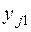
| … | 
| … | 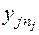
| 
| 
| 
|
| … | ||||||||
| k | 
| … | 
| … | 
| 
| 
| 
|
| Суммы по всем уровням | 
| 
| 
|
Результаты расчетов и выводы помещают в таблицу 2.
Таблица 2 — Схема дисперсионного анализа
| Источник изменчивости | Число степеней свободы | Суммы квадратов | Дисперсии | Критерий |
| Различие между уровнями Различие внутри уровней | f А = k – 1 f ош = N – k | SSA SS ош | 

| α =  F крит
F крит  влияет фактор
не влияет
влияет фактор
не влияет
|
После выполнения работы сделайте заключение о гипотезе Н 0 и факторе А.
ВАРИАНТ 1
Исследовалось влияние четырех различных типов покрытия на удельную проводимость телевизионных трубок. Результаты наблюдений:
| Наблюдения | ||||
Определить: влияет или не влияет тип покрытия на удельную проводимость.
ВАРИАНТ 2
Исследовалось влияние числа оборотов вращения центрифуги при нанесении слоя фоторезистора на его равномерность. Нанесение слоя фоторезистора осуществлялось на установке ПФН-2 на ситалловые подложки, покрытые металлическими пленками. Отклонения толщины слоя фоторезиста от среднего значения при различных частотах вращения центрифуги приведены в таблице:
| Частота вращения | Результаты наблюдений | |||||||
| 0,16 | 0,06 | 0,18 | 0,22 | 0,12 | 0,22 | 0,20 | 0,06 | |
| 0,04 | 0,12 | 0,14 | 0,04 | 0,06 | 0,16 | 0,06 | 0,08 | |
| 0,06 | 0,02 | 0,06 | 0,06 | 0,04 | 0,04 | 0,02 | 0,06 |
Определить: влияет или не влияет число оборотов вращения центрифуги на равномерность слоя резистора.
ВАРИАНТ 3
Проводился анализ технологического процесса растачивания отверстий Æ75+0,06 в шестернях на настроенном токарном станке. Для анализа из партии обрабатываемых деталей через равные промежутки времени было осуществлено пять выборок по шесть деталей в каждой. Отклонения от номинального размера деталей во всех выборках:
| Номер выборки | Номер детали | |||||
Определить, существует ли смещение центра рассеяния деталей, т.е. наличие систематической переменной погрешности.
ВАРИАНТ 4
Проведен эксперимент по оценке влияния постоянной влажности на эффективное сопротивление 10-омных резисторов, поступающих от четырех различных поставщиков.
| Поставщик | Результаты наблюдений | |||
Оценить: имеются ли статистически значимые различия между резисторами четырех поставщиков.
ВАРИАНТ 5
На трех станках изготавливаются детали одного и того же размера.
Из продукции каждого было отобрано по четыре образца. Предполагается, что выборки сделаны из нормальных совокупностей с одинаковыми дисперсиями.
Можно ли утверждать, что партии изготовляемых деталей имеют одинаковые групповые средние. Гипотезу проверить при α = 0,01, α = 0,05 и α = 0,10.
| Номер станка | Номера деталей | |||
ВАРИАНТ 6
Исследовать влияние способов измерения (I и II) параметров анодной алюминиевой фольги для электрических конденсаторов на точность измерения её удельной емкости.
| Способ измерения | Удельная емкость фольги, мкф/дм2 | ||||||
| 9,12 | 9,3 | 8,2 | 10,5 | 9,8 | 8,5 | 10,2 | |
| 8,34 | 8,58 | 8,18 | 8,42 | 8,66 | 8,26 | 8,5 |
Считая, что удельная емкость фольги распределена по гауссовскому закону, а образцы фольги принадлежат одному рулону, заформованному на одном агрегате при постоянных технологических режимах, требуется оценить различие систематических ошибок способов измерения.
ВАРИАНТ 7
Исследовалось влияние группы материалов одной и той же партии на выходную переменную У.
| Группа материалов | Выходная величина У | ||||||||
| 17,5 | 17,3 | 20,5 | 20,5 | ||||||
| 17,5 | 20,25 | 19,5 | 20,5 | 19,5 | 20,25 | ||||
| 20,5 | 19,5 | 19,25 | 19,5 | 19,5 | 20,5 | 19,5 | 19,7 | ||
| 19,5 | 20,5 | 19,3 | 19,5 | 19,3 | 20,2 |
Оценить значимость влияния и дать интерпретацию результатов эксперимента с конкретными рекомендациями.
ВАРИАНТ 8
В бригаде регулировщиков, состоящей из четырех человек, одному доверено личное клеймо контроля качества. Можно ли доверить личное клеймо бригаде в целом? Результаты контроля замеров по 8 аппаратам, отобранным с рабочих мест регулировщиков в полностью рандомизированном порядке, приведены в таблице.
| Регулировщик | ||||
| Значения выходного параметра аппарата | ||||
| 24,5 | 38,6 | 31,9 | 34,6 | |
| 31,2 | 28,9 | 27,3 | 30,5 | |
| 34,1 | 35,1 | 34,3 | 29,7 | |
| 32,3 | 30,6 | 28,3 | 32,3 | |
| 33,7 | 34,1 | 25,4 | 32,7 | |
| 27,6 | 30,2 | 29,6 | 31,2 | |
| 25,8 | 31,7 | 32,6 | 29,9 | |
| 31,2 | 28,5 | 29,4 | 30,1 |
Оценить: существует ли различие в качестве изделий у разных регулировщиков.
ВАРИАНТ 9
Одинаковая продукция шести предприятий исследовалась на надежность (среднее время безотказной работы). Из продукции каждого предприятия было отобрано по восемь образцов. Предполагается, что выборки сделаны из нормальных совокупностей с одинаковыми дисперсиями. Можно ли по групповым средним утверждать, что их продукция одинакового качества. Гипотезу проверить при α = 0,05 и α = 0,10.
| Номер предприятия | Номер изделия | |||||||
ВАРИАНТ 10
С четырех предприятий поступают партии конденсаторов одного и того же номинала. Из продукции каждого предприятия было отобрано по пять образцов. Предполагается, что выборки сделаны из нормальных совокупностей с одинаковыми дисперсиями.
Можно ли считать, что групповые средние этих партий одинаковы. Гипотезу проверить при α = 0,05 и α = 0,10.
| Номер предприятия | Номера деталей | ||||
ВАРИАНТ 11
На трех станках изготавливаются детали одного и того же размера.
Из продукции каждого было отобрано по четыре образца. Предполагается, что выборки сделаны из нормальных совокупностей с одинаковыми дисперсиями.
Можно ли утверждать, что партии изготовляемых деталей имеют одинаковые групповые средние. Гипотезу проверить при α = 0,01, α = 0,05 и α = 0,10.
| Номер станка | Номера деталей | |||
ВАРИАНТ 12
Испытывались на долговечность электрические лампы. Выборки были взяты из 4-х партий, изготовленных из разных материалов.
| Партии | Продолжительность горения в часах | |||||||
Гипотеза Н 0: Средние долговечности ламп в партиях одинаковы и не зависят от примененных материалов.
ВАРИАНТ 13
Проверялось наличие одинаковых систематических ошибок трех микроскопов, каждым из которых проводилось по пять измерений на одном и том же образце.
| Приборы | Отклонения в сотых долях микрона | ||||
| –4 | –2 | –21 | –4 | –4 | |
| +7 | +11 | +30 | +28 | +27 | |
| +19 | +2 | –13 | –9 | +2 |
Гипотеза Н 0: приборы имеют одинаковые систематические ошибки.
ВАРИАНТ 14
На предприятии, работающем в три смены, получены следующие данные о проценте брака выпускаемой продукции в каждой из смен за семь дней недели:
| Смена | Дни недели | ||||||
| 1,5 | 0,2 | ||||||
| 1,5 | 2,5 | 1,5 | |||||
| 1,5 | 1,5 |
Гипотеза Н 0: эффект влияния фактора А — смены на процент брака отсутствует.
ВАРИАНТ 15
С четырех предприятий поступают партии конденсаторов одного и того же номинала. Из продукции было отобрано по семь образцов. Предполагается, что выборки сделаны из нормальных совокупностей с одинаковыми дисперсиями.
Можно ли считать, что групповые средние этих партий одинаковы. Гипотезу проверить при α = 0,05 и α = 0,10.
| Номер предприятия | Номера деталей | ||||||
ВАРИАНТ 16
На трех станках изготавливаются детали одного и того же размера.
Из продукции было отобрано по четыре образца. Предполагается, что выборки сделаны из нормальных совокупностей с одинаковыми дисперсиями.
Можно ли утверждать, что партии изготовляемых деталей имеют одинаковые групповые средние. Гипотезу проверить при α= 0,01, α = 0,05 и α = 0,10.
| Номер станка | Номера деталей | |||
ВАРИАНТ 17
Три мастера проводили проверку однотипных устройств. Каждый из них проверил различное число комплектов и обнаружил различное число дефектов при каждой проверке. Анализируя их работу, начальник наладочного участка составил таблицу, из которой можно предположить, что 2-й мастер, вроде бы, имеет более низкую квалификацию или у него отсутствует служебное рвение, т.к. он обнаружил в среднем в два раза меньше дефектов (от общего среднего, равного 6). Можно ли на основании таблицы сделать вывод о различной квалификации мастеров?
Таблица результатов работы мастеров
| Проверка | Мастер | Всего | ||
| – – | – | |||
| Всего j -м мастером обнаружено дефектов. Выполнено проверок | ||||
| Среднее число найденных дефектов при одной проверке |
ВАРИАНТ 18
Выходной параметр — время нагревания микропаяльника, с. Уровни единственного фактора А — три разных типа микропаяльников. Эксперимент полностью рандомизирован.
Провести дисперсионный анализ и проверить гипотезу о том, что среднее время нагревания одинаково для всех типов микропаяльников.
| Тип микропаяльника | А 1 | А 2 | А 3 | |||
| Время нагревания микропаяльников, с | ||||||
ВАРИАНТ 19
Выходной параметр — срок службы миниатюрного индикаторного прибора, ч. Уровни единственного фактора А — партии приборов, изготовленные по четырем разным технологиям. Отбор приборов для испытания полностью рандомизирован. Было отобрано по 5 приборов из каждой партии.
Проверить нуль-гипотезу о том, что варианты технологического процесса не влияют на срок службы индикаторных приборов.
| Номер варианта технологического процесса | Приборы | ||||
| А1 А2 А 3 А4 |
ВАРИАНТ 20
Задача технолога — выбрать оптимальный вариант (из трёх предложенных) конструкции механизма подачи и направления провода для полуавтомата намотки контурных катушек радиоприемников. В качестве выходного параметра была замерена добротность катушек опытной партии с эталонным сердечником. Проверить нуль-гипотезу о том, что вариант механизма не влияет на добротность катушек. Для упрощения расчетов использовать подходящий код. Отбор по 10 катушек из серий опытной партии полностью рандомизирован. Данные замеров приведены в таблице.
| Тип механизма | А 1 | А 2 | А 3 | |||
| Добротность катушек | ||||||
ВАРИАНТ 21
Для изготовления печатных плат на складе завода получены две партии химиката, сертификаты на которые потеряны. Выяснить, являются ли эти партии химиката пригодными для использования в технологическом процессе, если на складе находится еще одна партия того же химиката, принятая по сертификату входным контролем. Данные замеров поверхностного сопротивления восьми контрольных экземпляров серий печатных плат, отбор которых был полностью рандомизирован, в кодированном виде представлены в таблице.
| Номер партии химиката | А 1 | А 2 | А 3 | |||
| Поверхностное сопротивление (кодированное) | –17 –28 –7 | –27 –18 | –13 | –32 –19 | ||
ВАРИАНТ 22
Для пропитки высокочастотных катушек индуктивности радиоприемника получен парафин, марка которого не соответствует записанной в технической документации. Задача технолога — решить, можно ли эту партию парафина (партия № 1) запустить в производство без ущерба для качества изделий. Для проведения контрольных замеров партия № 1 парафина была запущена параллельно текущему производству, где использовались еще две партии. Эксперимент полностью рандомизирован. Из каждой партии отобрано по 8 катушек.
| Номер партии парафина | А 1 | А 2 | А 3 | |||
| Добротность катушек | ||||||
Контрольная работа № 2
Целью контрольной работы является освоение методики планирования и обработки результатов активного эксперимента на примере полного факторного эксперимента.
Такой эксперимент выполняется для получения математического описания (модели) исследуемого процесса или объекта.
Модель, по плану 1-го порядка, находится в форме линейного уравнения регрессии
 (1)
(1)
или квазилинейного уравнения регрессии
 (2)
(2)
В заданиях даны натуральные значения факторов и приведены результаты эксперимента.
При выполнении работы необходимо вначале составить матрицу планирования эксперимента (план эксперимента), в которой указываются порядок проведения двух или трёх параллельных опытов и значения факторов в каждом опыте. Параллельные опыты проводятся для исключения влияния неконтролируемых факторов на результаты экспериментов.
Последовательность проведения опытов в каждой серии устанавливается с помощью таблиц случайных чисел.
Значения факторов указываются в кодированном виде
 (3)
(3)
где 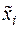 — натуральное (действительное) значение фактора;
— натуральное (действительное) значение фактора;
 — базовый (основной) уровень фактора;
— базовый (основной) уровень фактора;
 — шаг варьирования фактора.
— шаг варьирования фактора.
В матрицу планирования вводится фиктивная переменная хо, которая во всех опытах принимает значения +1. Введение этой переменной позволяет свести уравнения регрессии к удобному для использования виду

В матрице планирования единицы не записываются, а проставляются только плюс или минус в соответствии с правилами чередования знаков факторов в каждом опыте.
Затем проводится эксперимент в соответствии с планом и наблюдаемые значения выходного параметра y записываются в таблицу.
После проведения эксперимента проводится обработка его результатов, которая содержит:
– проверку воспроизводимости опытов;
– расчет коэффициентов регрессии;
– проверку значимости коэффициентов регрессии;
– построение математической модели;
– проверку адекватности модели результатам эксперимента;
– построение математической модели для действительных (натуральных) значений факторов.
Проверка воспроизводимости опытов проводится по критерию Кохрена
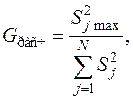
где  — выборочная дисперсия выходного параметра в j -м опыте;
— выборочная дисперсия выходного параметра в j -м опыте;
 — максимальная выборочная дисперсия выходного параметра;
— максимальная выборочная дисперсия выходного параметра;
N — количество опытов.

где g — номер серии параллельных опытов (1, 2, 3);
m — количество серий параллельных опытов (2 или 3);
 — измеренное значение выходного параметра в серии параллельных опытов;
— измеренное значение выходного параметра в серии параллельных опытов;
 — среднее значение выходного параметра в j -м опыте.
— среднее значение выходного параметра в j -м опыте.
Полученное расчётное значение критерия Кохрена  сравнивается с его табличным значением
сравнивается с его табличным значением  , которое находится при числе степеней свободы
, которое находится при числе степеней свободы  и
и  и заданном уровне значимости α.
и заданном уровне значимости α.
Если  <
<  , то гипотеза об однородности дисперсий принимается. Это значит, что условия проведения опытов одинаковы (воспроизводимы) и отклонения выходного параметра случайны.
, то гипотеза об однородности дисперсий принимается. Это значит, что условия проведения опытов одинаковы (воспроизводимы) и отклонения выходного параметра случайны.
Если  ≥
≥  , то отклонения максимальной дисперсии от остальных не случайны и, следовательно, опыты не воспроизводимы, т.е. имеется доминирующий фактор. В таблице 1 делается вывод: дисперсии однородны или не однородны.
, то отклонения максимальной дисперсии от остальных не случайны и, следовательно, опыты не воспроизводимы, т.е. имеется доминирующий фактор. В таблице 1 делается вывод: дисперсии однородны или не однородны.
Расчет коэффициентов регрессии при ортогональном плане эксперимента проводится по формуле

где i — номер фактора (параметра), i = 0, k;
 — значение i -го фактора в j -м опыте (+1, –1).
— значение i -го фактора в j -м опыте (+1, –1).
Поскольку факторы в опытах имеют кодированные значения +1 или –1, то для вычисления коэффициентов регрессии 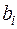 нужно при суммировании каждому значению
нужно при суммировании каждому значению  в j -м опыте просто приписывать знак i -го фактора в этом опыте. Аналогично определяются коэффициенты
в j -м опыте просто приписывать знак i -го фактора в этом опыте. Аналогично определяются коэффициенты  для эффектов взаимодействия.
для эффектов взаимодействия.
Проверка значимости коэффициентов регрессии проводится по критерию Стьюдента


где 

Оценка  одинакова для всех коэффициентов регрессии.
одинакова для всех коэффициентов регрессии.
Дисперсия воспроизводимости опытов по выборочным дисперсиям выходного параметра равна

Для коэффициентов эффектов взаимодействия

Расчетное значение t -критерия Стьюдента сравнивается с его табличным значением t крит, которое определяется при числе степеней свободы  и уровне значимости α. Для всех коэффициентов в данном эксперименте t крит одинаково.
и уровне значимости α. Для всех коэффициентов в данном эксперименте t крит одинаково.
Если найденный для коэффициента регрессии критерий ti расч > t крит, то данный коэффициент регрессии является статистически значимым. Незначимы будут коэффициенты, для которых ti расч < t крит. Соответственно в выводах табл. 1 оставляем ЗН или НЗМ.
Построение математической модели исследуемого процесса (объекта) проводится в соответствии с результатами проверки значимости коэффициентов регрессии: члены уравнения, содержащие незначимые коэффициенты регрессии, исключаются.
Линейное уравнение регрессии (1) записывается в правой нижней части таблицы 1. Нелинейное (квазилинейное) уравнение регрессии записывается в левой нижней части таблицы 1. Если все коэффициенты регрессии для эффектов взаимодействия оказались незначимыми, то нелинейное уравнение регрессии не записывается.
Проверка адекватности математической модели результатам эксперимента проводится по F -критерию Фишера

где  — дисперсия адекватности.
— дисперсия адекватности.
Вначале проводится проверка линейного уравнения регрессии. Если оно не адекватно, то проверяется нелинейное уравнение регрессии.
Для проверки адекватности необходимо по составленной математической модели рассчитать оценку выходного параметра  для каждого опыта путем подстановки кодированных значений факторов (+1, –1), которые они имеют в соответствующем опыте. Если проверяются обе модели (линейная и нелинейная), то результаты вычислений
для каждого опыта путем подстановки кодированных значений факторов (+1, –1), которые они имеют в соответствующем опыте. Если проверяются обе модели (линейная и нелинейная), то результаты вычислений  записываются в таблицу 1 в виде дроби: в числителе для линейной модели и в знаменателе для нелинейной модели.
записываются в таблицу 1 в виде дроби: в числителе для линейной модели и в знаменателе для нелинейной модели.
Затем вычисляется дисперсия адекватности

где d — число линейных членов аппроксимирующего полинома (уравнения регрессии). Результаты вычисления 
 и F расч в таблице 1 также записываются дробью для двух моделей.
и F расч в таблице 1 также записываются дробью для двух моделей.
Расчетное значение F -критерия сравнивается с табличным F крит, которое находится при заданном уровне значимости α и степенях свободы 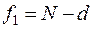 и
и  .
.
Если F расч < F крит, то принимается гипотеза об адекватности построенной математической модели результатам эксперимента. Если F расч > F крит, то гипотеза отвергается: линейная (или нелинейная) модель не адекватна результатам эксперимента. В этом случае переходят к построению плана второго порядка для получения квадратичной модели.
Построение математической модели для действительных (натуральных) значений факторов выполняется путем подстановки в полученную математическую модель кодированных значений факторов в виде (3). Из задания известны номинальные величины факторов в виде базового (основного) уровня  и интервалы изменения факторов (шаг варьирования). После преобразования получаем уравнение регрессии для действительных (натуральных) значений факторов
и интервалы изменения факторов (шаг варьирования). После преобразования получаем уравнение регрессии для действительных (натуральных) значений факторов
 или
или  ,
,
где 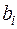 и
и  — новые значения коэффициентов регрессии.
— новые значения коэффициентов регрессии.
В этих уравнениях вместо x и y должны быть записаны обозначения действительных параметров.
В отчете по работе (в тексте) должны быть представлены все расчеты, результаты которых записаны в таблицу. В тексте достаточно также привести примеры расчета одной строки таблицы, соответствующей какому-либо номеру опыта, одного коэффициента регрессии. Порядок расчетной записи: формула, формула с подставленными числами, ответ.
 Таблица 1 — Таблица планирования и обработки результатов активного эксперимента
Таблица 1 — Таблица планирования и обработки результатов активного эксперимента
| Результаты эксперимента и проверка воспроизводимости | Проверка адекватности | |||||||||||||||||||||||||||||
| № опы та | Порядок проведения опытов | Матрица планирования | Эффекты взаимодействия |

|

|

|

|

|

|

| ||||||||||||||||||||
| х0 | х1 | х2 | х3 | х1 х2 | х1 х3 | х2 х3 | х1 х2 х3 | |||||||||||||||||||||||

| ||||||||||||||||||||||||||||||

| 
| 
| ||||||||||||||||||||||||||||

| 
| 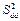
| ||||||||||||||||||||||||||||

| Проверка значимости коэффициентов | 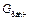
| 
| |||||||||||||||||||||||||||
| α |  = =
| α | 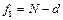
| |||||||||||||||||||||||||||

| 
| 
| 
| |||||||||||||||||||||||||||

| 
| 
| α | |||||||||||||||||||||||||||
| Вывод | нзн | нзн | нзн | нзн | нзн | нзн | нзн | нзн | 
| 
| ||||||||||||||||||||
| Нелинейное уравнение регрессии | Вывод | 
| Вывод | 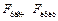
| ||||||||||||||||||||||||||
| Дисперсии (не) однородны | Описание (не) адекватно | |||||||||||||||||||||||||||||
| Линейное уравнение регрессии | ||||||||||||||||||||||||||||||
ВАРИАНТ 1
Исследовать процесс получения резистивных плёнок рения. На основании анализа технологического процесса и результатов предварительных опытов установлено, что на ТKC плёнок рения оказывают влияние температура испарения (А); температура подложки при осаждении (В) и термообработке (С) плёнок. Исследование технологического процесса для получения локального описания поверхности отклика осуществляется с помощью ПФЭ типа 23. Проводилось две серии параллельных опытов (y = –ТКС×104 1/°С).






