Регрессионный анализ (РА) используется для получения математического описания (модели) процесса в виде уравнения регрессии и оценки коэффициентов этого уравнения (коэффициентов регрессии).
Это связано с тем, что физические (аналитические) модели ряда процессов (например, технологических) либо отсутствуют, либо оказываются непригодными. Такая ситуация возникает в том случае, когда имеет место неполное знание механизма процесса. Соответственно, оказывается неизвестным и аналитическое выражение функции, связывающей показатель качества y с переменными (факторами) xi. Поэтому приходится ограничиваться представлением функции статистической моделью в виде полинома или уравнения регрессии
где b — теоретические коэффициенты регрессии, которые неизвестны.
Пользуясь результатами эксперимента, можно определить только выборочные коэффициенты регрессии b 0, bi и др., которые являются лишь оценками теоретических коэффициентов регрессии. Определить эти искомые оценки можно методом максимального правдоподобия или методом наименьших квадратов.
Уравнение регрессии, полученное на основе эксперимента, имеет вид
где 
— выборочная оценка для генерального значения y ген.
Степень уравнения регрессии зависит от формы (характера) связи между переменными, которая определяется в результате корреляционного анализа или путём визуального построения линий регрессии на корреляционном поле по опытным данным. Для этого на корреляционном поле наносят результаты эксперимента и через них «на глазок» проводят некоторую линию (прямую или кривую). По виду этой линии (рис. 2.4) подбирают уравнение, соответствующее форме зависимости на корреляционном поле. Это и будет уравнение регрессии.
Эти линии проводятся так, чтобы сумма квадратов отклонений опытных данных от этой линии была минимальной. Это достигается путём соответствующего определения коэффициентов регрессии по методу наименьших квадратов (МНК):
где yi — ордината точки на корреляционном поле, соответствующая опытным данным;
n — количество опытов (объем выборки);
— ордината соответствующей точки на линии регрессии 
(средняя y для данного значения x) (рис. 2.5).
| 
|
Рисунок 2.4 — Корреляционные поля для различных
зависимостей у=f (х)
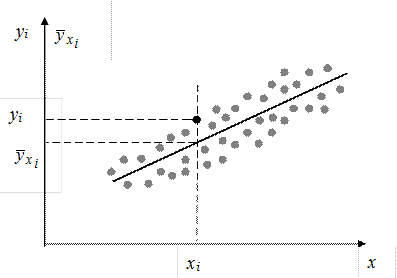
Рисунок 2.5 — Ординаты точек yi и 
Задача состоит в выборе неизвестных b 0, b 1,…, bk так, чтобы гиперплоскость, описываемая уравнением регрессии, оптимальным образом проходила через облако экспериментальных точек и расстояния от точек до плоскости были минимальными. Для этой цели приравниваются нулю частные производные от суммы S по неизвестным коэффициентам регрессии
Получаем систему нормальных уравнений, из которой и определяют коэффициенты регрессии [16, 22].
Следует иметь в виду, что при k > 3 и большой выборке составление такой системы уравнений и её решение проводятся на ЭВМ.
Рассмотрим регрессионный анализ для случая одного фактора, k = 1.
Уравнение регрессии имеет вид:
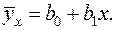
Согласно МНК составляют сумму квадратов отклонений экспериментальных данных от линии регрессии
Берём частные производные по коэффициентам регрессии и приравниваем их нулю.
