Статистический анализ используется для оценки параметров (статистик) распределений опытных данных, подбора закона их распределения, проверки статистических гипотез.
Метод достаточно подробно разработан в математической статистике [3, 8, 9]. Для определения параметров распределения используются:
1. Метод моментов.
2. Метод максимального правдоподобия.
Рассмотрим метод максимального правдоподобия, который может применяться только при известном законе распределения случайной величины. Метод максимального правдоподобия был предложен Гауссом и обобщен Р. Фишером.
В основе метода лежит функция правдоподобия. Метод даёт наиболее точные оценки, но они могут быть смещёнными. Смещение, однако, может быть устранено введением поправок или увеличением объёма эксперимента (объема выборки).
Правдоподобие определённой системы наблюдаемых величин есть вероятность получения таких величин, основанная на заданной теоретической модели с определёнными параметрами q1, q2, …, q k. Тогда оценки максимума правдоподобия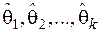 
есть те величины определённых параметров q1, q2, …, q k, которые максимизируют правдоподобие, т.е. те величины параметров q j, которые представляются наиболее вероятными на основе представленных данных. Суть метода заключается в составлении функции правдоподобия, которая представляет собой произведение вероятностей. Она составляется для дискретных и непрерывных случайных величин.
При составлении функции правдоподобия для дискретных случайных величин в качестве закона распределения используется зависимость вероятности наступления события р (xi,q):
,
где xi — значения дискретной случайной величины X, которая в результате проведения опытов приняла значения x 1, x 2, …, xn;
q — неизвестный параметр теоретического закона распределения, который необходимо оценить.
При составлении функции правдоподобия для непрерывной случайной величины в качестве закона распределения используется плотность распределения случайной величины f (xi, q1, q2, …, q k):
где n — количество измеренных значений случайной величины xi (объём выборки);
— неизвестный параметр теоретического распределения, который следует оценить;
k — количество неизвестных параметров распределения.
В обоих случаях за оценку q принимается такое точечное значение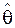 
, которое обеспечивает максимум функции правдоподобия. Это имеет место в том случае, когда частная производная от функции правдоподобия будет равна нулю, т.е.
.
Таким образом, неизвестные параметры q j функции распределения, которые необходимо оценить, определяются там, где L — функция достигает максимума. Это положение необходимо проверить путём взятия частной производной второго порядка 
, которая в случае точки максимума должна быть отрицательной.
Однако дифференцирование произведения, имеющего большое число сомножителей, крайне затруднительно. Поэтому находят не максимум функции L, а максимум функции ln L, т.е. берут производную от логарифма функции правдоподобия
.
Количество уравнений равно k, что позволяет определить k неизвестных параметров q. Для проверки принадлежности найденной оценки максимуму функции ln L необходимо взять вторую производную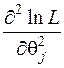 
, которая должна быть отрицательной.
Оценки получаются состоятельными и эффективными.
Недостатки метода:
1. Должен быть известен заранее закон распределения случайной величины.
2. По этому методу иногда получаются очень сложные уравнения. Особенно это имеет место, когда количество параметров k ³ 2.
3. Смещенные оценки.
