Полный факторный эксперимент

 

Полный факторный эксперимент (ПФЭ) — это эксперимент, в котором осуществляется перебор всех возможных сочетаний уровней факторов.

Фиксированный набор уровней факторов определяет одно из возможных состояний системы («черного ящика»). Одновременно это есть условия проведения одного из возможных опытов. Если перебрать все возможные сочетания уровней факторов х_i системы, то получим множество состояний системы. Каждому состоянию соответствует какое-то значение параметра оптимизации y_j.

Это будет одновременно число возможных различных опытов. Число возможных состояний определяет сложность данной системы.

Если число уровней фактора х_i равно m_i, то число возможных состояний системы, содержащей k факторов, равно m ₁ּ m ₂ ּ …× m_k.

В случае равенства числа уровней факторов m = m ₁= m ₂ = …= m_k имеем ПФЭ типа m^k. Одновременно это будет количество опытов N = m^k (фиктивный фактор х ₀ не учитывается).

Самым простым является ПФЭ для линейной модели, при получении которой каждый фактор из k достаточно менять в двух уровнях (m = 2). Имеем ПФЭ типа 2^k.

Если взять k =2 факторам, то будет ПФЭ типа 2². Следовательно, число опытов в такой системе будет N = 4, для которых нетрудно написать все возможные сочетания уровней факторов в эксперименте. Матрица планирования эксперимента (МПЭ) приведена в таблице 3.2.

 

Таблица 3.2 — ПФЭ типа 2²

 

Номер опыта	х 0	х 1	х 2	y	Кодовое обозначение строк
	+ + + +	– + – +	– – + +	y 1 y 2 y 3 y 4	a b ab

 

Геометрическая интерпретация этого плана представлена на рис. 3.2.

 

 

Рисунок 3.2 — Расположение «опытных точек» при k =2

 

На рисунке обозначены:

— натуральные значения факторов;

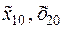— основные уровни факторов;

0 — центр плана (основной уровень);

х ₁ и х ₂ — кодированные значения факторов.

Оси координат кодированных значений факторов проводятся параллельно осям координат натуральных значений факторов. Масштабы по новым осям координат выбираются так, чтобы интервалы изменения факторов были равны ±1. На плоскости получим квадрат, вершины которого соответствуют условиям проведения опытов. (Номера опытов в МПЭ и номера вершин квадрата совпадают). Внутри квадрата расположена область эксперимента.

Если число факторов k = 3, то областью эксперимента будет куб (2³), а условия проведения опытов будут соответствовать вершинам куба и т.д.

План, представленный в МПЭ для получения линейной модели, может быть записан в матричной форме Y = X ּ B, где Y — матрица результатов опытов, X — матрица планирования опытов, B — матрица коэффициентов линейного уравнения регрессии.

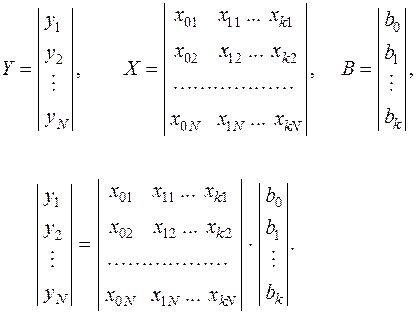
Для уменьшения громоздкости записи условий проведения опытов вместо МПЭ, которая обладает несомненной наглядностью, используют буквенные обозначения строк МПЭ (см. табл. 3.2). Для этого каждому фактору ставят в соответствие строчные буквы латинского алфавита: х ₁ ® а, х ₂ ® в, х ₃ ® с и т.д., если факторы находятся на верхнем уровне. Факторы на нижнем уровне никак не обозначают. Если все факторы в какой-либо строке МПЭ находятся на нижнем уровне, то такое состояние обозначают единицей, если на верхнем уровне, то произведением букв. Тогда строчная запись МПЭ будет (1), а, в, ав. Такая запись тем эффективнее, чем больше факторов (k).

Для построения МПЭ при k > 2…3, т.е. перебора всех возможных сочетаний уровней факторов, существует ряд приемов [15, 16]. Одно из правил построения МПЭ: первая строка матрицы выбирается так, чтобы все управляемые переменные находились на нижнем уровне (–); частота смены знака управляемой переменной для каждой последующей переменной вдвое меньше, чем для предыдущей (см. табл. 3.2).

Для построения линейной модели, как указывалось ранее, достаточно изменять факторы на двух уровнях. Этого же достаточно для построения модели неполного высшего порядка (квазилинейной)

,

т.е. если два фактора, то

y = b ₀ + b ₁ x ₁ + b ₂ x ₂ + b ₃ x ₁ × x _2,

если три фактора, то

y = b ₀ + b ₁ × x ₁ + b ₂ × x ₂ + b ₃ × x ₃ + b ₁₂ × x ₁ × x ₂ + b ₁₃ × x ₁ × x ₃ + b ₂₃ × x ₂ × x ₃ +

+ b ₁₂₃ × x ₁ × x ₂ × x ₃и т.д.

В приведенных уравнениях b_i× x_i — линейные члены уравнения регрессии, остальные члены — это взаимодействия двух или трех факторов. Они носят название эффект взаимодействия первого порядка — b_ij× x_i× x_j и эффект взаимодействия второго порядка — b_ijl× x_i× x_j × x_l. Например, в приведенном выше уравнении регрессии для трех факторов могут существовать три двойных и один тройной эффекты взаимодействия. МПЭ при этом имеет вид (табл. 3.3). В связи с этим вводятся понятия «эффект фактора» и «эффект взаимодействия».

 

 

Таблица 3.3 — ПФЭ типа 2³

 

№ опыта	План эксперимента	Эффекты взаимодействия	y
х 0	х 1	х 2	х 3	х 1 х 2	х 1 х 3	х 2 х 3	х 1 х 2 х 3
. . .	+ +	– +	– –	– –	+ –	+ –	+ +	– +	y 1 y 2 . . .

 

Эффект фактора — это вклад фактора в величину параметра оптимизации при переходе фактора от нижнего уровня к верхнему (линейный, основной или главный эффект). Этот эффект численно равен удвоенному коэффициенту b_i уравнения регрессии, поскольку переход фактора с нулевого уровня на верхний или нижний определяется коэффициентом b_i.

Эффект взаимодействия — это эффект, который имеет место в том случае, когда эффект одного фактора зависит от уровня, на котором находится другой фактор. Этот эффект численно равен удвоенному коэффициенту полинома b_ij, если эффект взаимодействия первого порядка, или коэффициенту b_ijl, если эффект взаимодействия второго порядка.

ПФЭ позволяет оценить линейные эффекты и эффекты взаимодействия, т.е. определить коэффициенты полинома: линейной части — b_i, взаимодействий парных (первого порядка) — b_ij и других (более высокого порядка).

Планы ПФЭ являются ненасыщенными, т.е. число опытов в них может существенно превышать число опытов, необходимых для определения неизвестных коэффициентов регрессии. Например, при k = 4, число опытов будет N = 2 ^k = 2⁴ = 16, а число неизвестных коэффициентов для линейной модели равно 5. Это значит, что число опытов в три раза больше необходимого, что не эффективно, поскольку ведет к неоправданному расходу времени и средств.

 

3.4 Свойства матрицы ПФЭ типа 2 ^k

 

Отметим, что эти свойства не зависят от числа факторов k и определяют качество модели, которая должна быть оптимальной. Всего таких свойств четыре: два из них следуют из построения МПЭ и являются свойствами отдельных столбцов, третье — следствие совокупности столбцов и четвертым должна обладать матрица [15].

1. Симметричность относительно центра плана: алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю

где i — номер фактора, ,

N — количество опытов.

2. Условие нормировки: сумма квадратов элементов каждого вектор-столбца равна числу опытов

в связи с тем, что значения факторов в матрице составляют ±1.

3. Ортогональность матрицы: сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю

Планы, имеющие такое свойство, называются ортогональными. Это очень важное свойство, так как при его выполнении значительно уменьшаются трудности вычисления коэффициентов регрессии. Ортогональные планы позволяют определять коэффициенты регрессии независимо друг от друга.

4. Ротатабельность — точки, в которых проводятся опыты, в МПЭ располагаются таким образом, что точность предсказания значений параметра оптимизации (y) одинакова на равных расстояниях от центра плана и не зависит от направления. Планы, обладающие таким свойством, называются ротатабельными (ротация — круговращение). Ротатабельность означает, что предсказанные значения параметра оптимизации имеют одинаковую дисперсию.

МПЭ, имеющая указанные свойства, называется оптимальной, а ПФЭ типа 2 ^k является оптимальным при построении линейной модели.