Требуется распределить имеющиеся В единиц средств среди n предприятий, доход gi (xi) от которых, в зависимости от количества вложенных средств хi, определяется матрицей (n ´ n), приведенной в табл. 19.1, так, чтобы суммарный доход со всех предприятий был бы максимальным.
Таблица 19.1
| x gi | g1 | g2 | … | gi | … | gn |
| x1 | g1(x1) | g2(x1) | … | gi(x1) | … | gn(x1) |
| x2 | g1(x2) | g2(x2) | … | gi(x2) | … | gn(x2) |
| … | … | … | … | … | … | … |
| xi | g1(xi) | g2(xi) | … | gi(xi) | … | gn(xi) |
| … | … | … | … | … | … | … |
| xn | g1(xn) | g2(xn) | … | gi(xn) | … | gn(xn) |
Запишем математическую модель задачи.
Определить X* = (
, 
, …, 
, …, 
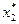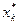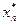), удовлетворяющий условиям
, (19.1)
(19.2)
и обеспечивающий максимум целевой функции
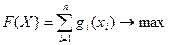(19.3)
Очевидно, эта задача может быть решена простым перебором всех возможных вариантов распределения В единиц средств по n предприятиям, например на сетевой модели. Однако решим ее более эффективным методом, который заключается в замене сложной многовариантной задачи многократным решением простых задач с малым количеством исследуемых вариантов.
С этой целью разобьем процесс оптимизации на n шагов и будем на каждом k -м шаге оптимизировать инвестирование не всех предприятий, а только предприятий с k -го по n -е. При этом естественно считать, что в остальные предприятия (с первого по (k –1)-е тоже вкладываются средства, и поэтому на инвестирование предприятий с k -го по n -е остаются не все средства, а некоторая меньшая сумма Сk ≤ В. Эта величина и будет являться переменной состояния системы. Переменной управления на k -м шаге назовем величину хk средств, вкладываемых в k -e предприятие. В качестве функции Беллмана Fk (Ck) на k -м шаге можно выбрать максимально возможный доход, который можно получить с предприятий с k -го по n -е при условии, что на их инвестирование осталось Сk средств. Очевидно, что при вложении в k -e предприятие хk средств будет получена прибыль gk (xk), а система к (k +1)-му шагу перейдет в состояние Sk +1 и, следовательно, на инвестирование предприятий с (k +1)-го до n -го останется Сk +1 = (Сk – хk) средств.
Таким образом, на первом шаге условной оптимизации при k = n функция Беллмана представляет собой прибыль только с n -го предприятия. При этом на его инвестирование может остаться количество средств Сn, 0≤ Сn ≤ В. Чтобы получить максимум прибыли с этого предприятия, можно вложить в него все эти средства, т. е. Fn (Сn) = gn (Сn) и хn = Сn.
На каждом последующем шаге для вычисления функции Беллмана необходимо использовать результаты предыдущего шага. Пусть на k -м шаге для инвестирования предприятий с k -го по n -е осталось Сk средств (0≤ Сk ≤ В). Тогда от вложения в k -e предприятие хk средств будет получена прибыль gk (Ck), а на инвестирование остальных предприятий (с k -го по n -е) останется Сk +1 = (Сk – хk) средств. Максимально возможный доход, который может быть получен с предприятий (с k -го по n -е), будет равен:
(19.4)
Максимум выражения (9.4) достигается на некотором значении 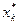, которое является оптимальным управлением на k -м шаге для состояния системы Sk. Действуя таким образом, можно определить функции Беллмана и оптимальные управления до шага k = 1.
Значение функции Беллмана F 1(С 1) представляет собой максимально возможный доход со всех предприятий, а значение , на котором достигается максимум дохода, является оптимальным количеством средств, вложенных в первое предприятие. Далее на этапе безусловной оптимизации для всех последующих шагов вычисляется величина Сk = (Сk -1 – хk -1) оптимальным управлением на k -м шаге является то значение хk, которое обеспечивает максимум дохода при соответствующем состоянии системы Sk.
Пример 1. На развитие трех предприятий выделено 5 млн. руб. Известна эффективность капитальных вложений в каждое предприятие, заданная значением нелинейной функции gi (xi), представленной в табл. 19.2.
Таблица 19.2
| x | g 1 | g 2 | g 3 |
| 2,2 | 2,8 | ||
| 3,2 | 5,4 | ||
| 4,1 | 4,8 | 6,4 | |
| 5,2 | 6,2 | 6,6 | |
| 5,9 | 6,4 | 6,9 |
Необходимо распределить выделенные средства между предприятиями таким образом, чтобы получить максимальный суммарный доход.
Для упрощения расчетов предполагаем, что распределение средств осуществляется в целых числах xi = {0, 1, 2, 3, 4, 5} млн. руб.
Решение.
I этап. Условная оптимизация.
1-й шаг: k = 3. Предположим, что все средства в количестве x3 = 5 млн. руб. отданы третьему предприятию. В этом случае максимальный доход, как это видно из табл. 19.3, составит g 3(x 3) = 6,9 тыс. руб., следовательно: F 3(C3) = g 3(x 3).
Таблица 19.3
| x 3 C 3 | F 3(C 3) |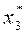 
| ||||||
| 2,8 | 2,8 | |||||||
| 5,4 | 5,4 | |||||||
| 6,4 | 6,4 | |||||||
| 6,6 | 6,6 | |||||||
| 6,9 | 6,9 |
2-й шаг: k = 2. Определяем оптимальную стратегию при распределении денежных средств между вторым и третьим предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:
,
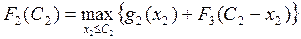на основе которого составлена табл. 19.4.
Таблица 19.4
| х 2 С 2 | F 2(C 2) | 
| ||||||
| 0 + 0 | ||||||||
| 0 + 2,8 | 2 + 0 | 2,8 | ||||||
| 0 + 5,4 | 2 + 2,8 | 3,2 + 0 | 5,4 | |||||
| 0 + 6,4 | 2 + 5,4 | 3,2 + 2,8 | 4,8 + 0 | 7,4 | ||||
| 0 + 6,6 | 2 + 6,4 | 3,2 + 5,4 | 4,8 + 2,8 | 6,2 + 0 | 8,6 | |||
| 0 + 6,9 | 2 + 6,6 | 3,2 + 6,4 | 4,8 + 5,4 | 6,2 + 2,8 | 6,4 + 0 | 10,2 |
3-й шаг: k = 1. Определяем оптимальную стратегию при распределении денежных средств между первым и двумя другими предприятиями, используя следующую формулу для расчета суммарного дохода:
,
на основе которого составлена табл. 19.5.
Таблица 19.5
| х 1 С 1 | F 1(C 1) | 
| ||||||
| 0 + 0 | ||||||||
| 0 + 2,8 | 2,2 + 0 | 2,8 | ||||||
| 0 + 5,4 | 2,2 + 2,8 | 3 + 0 | 5,4 | |||||
| 0 + 7,4 | 2,2 + 5,4 | 3 + 2,8 | 4,1 + 0 | 7,6 | ||||
| 0 + 8,6 | 2,2 + 7,4 | 3 + 5,4 | 4,1 + 2,8 | 5,2 +0 | 9,6 | |||
| 0 + 10,2 | 2,2 + 8,6 | 3 + 7,4 | 4,1 + 5,4 | 5,2 + 2,8 | 5,9 + 0 | 10,8 |
II этап. Безусловная оптимизация.
Определяем компоненты оптимальной стратегии.
1-й шаг. По данным из табл. 9.5 максимальный доход при распределении 5 млн. руб. между тремя предприятиями составляет: C 1 = 5, F 1(5) = 10,8.
При этом первому предприятию нужно выделить = 1 млн руб.
2-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего предприятий: С 2 = C 1 – = 5 – 1 = 4 млн руб.
По данным табл. 9.4 находим, что оптимальный вариант распределения денежных средств размером 4 млн. руб. между вторым и третьим предприятиями составляет: F 2(4) = 8,6 при выделении второму предприятию 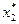= 2 млн руб.
3-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю третьего предприятия: С 3 = C 2 – 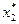= 4 – 2 = 2 млн руб.
По данным табл. 9.3 находим: F 3(2) = 5,4 и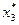 
= 2 млн руб.
Таким образом, оптимальный план инвестирования предприятий:
Х* = (1, 2, 2), который обеспечит максимальный доход, равный
F (5) = g1 (l) + g2 (2) + g3 (2) = 2,2 + 3,2 + 5,4 = 10,8 млн руб.
