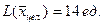Метод Гомори и его применение в экономических задачах

Целочисленное решение может быть найдено с использованием алгоритма, предложенного Гомори, который состоит в следующем.

Симплексным методом находят оптимальное решение задачи. Если решение целочисленного, то задача решена. Если же оно не целочисленное и содержит хотя бы одну дробную координату, то накладывают дополнительное ограничение по целочисленности и вычисления продолжают до получения нового решения. Если и оно является не целочисленным, то вновь накладывают дополнительное ограничение по целочисленности. Вычисления продолжают до тех пор, пока не будет получено целочисленное решение или показано, что задача не имеет целочисленного решения.

Пусть получено оптимальное решение , которое не является целочисленным, тогда последний шаг симплексной таблицы имеет следующий вид:

х 1			¼		¼		h 1,r+1	¼	h 1,n	f 1
х 2			¼		¼		h 2,r+1	¼	h 2,n	f 2
¼	¼	¼	¼	¼	¼	¼	¼	¼	¼	¼
х i			¼		¼		hi ,r+1	¼	hi ,n	fi
¼	¼	¼	¼	¼	¼	¼	¼	¼	¼	¼
х r			¼		¼		h r,r+1	¼	h r,n	f r

 

где r – ранг системы ограничений;

h _i,r+1 – коэффициент симплексной таблицы i –й строки, r + 1 столбца;

f_i – свободный член i –й строки.

Пусть f_i и хотя бы одно h_ij ()– дробные числа.

Обозначим [ f_i ] и [ h_ij ] – целые части чисел f_i и h_ij.

Целой часть числа f_i называют наибольшее целое число, не превосходящее числа f_i.

Дробную часть чисел f_i и h_ij обозначим { f_i } и { h_ij }, она определяется следующим образом:

{ f_i } = f_i – [ f_i ], { h_ij } = h_ij – [ h_ij ].

Если f_i и хотя бы одно значение h_ij дробное, то с учетом введенных обозначений целых и дробных чисел дополнительное ограничение по целочисленности примет вид

{ h_{i ,r+1}} x _r+1 + { h_{i ,r+2}} x _r+2 + ¼ +{ h_{i , n} } x_n > { f_i }.

 

Примечание 1. Если f_i дробное, а все h_ij целые, то задача не имеет целочисленного решения.

Примечание 2. Ограничение целочисленности может быть наложено не на все переменные, а лишь на их часть. В этом случае задача является частично целочисленной.

 

Решим пример методом Гомори.

Математическая модель задачи:

при ограничениях:

.

Решение задачи симплексным методом представлено в табл. 17.1.

 

Таблица 17.1.

ci	БП					bi
х 1	х 2	х 3	х 4
	х 3					19/3
	х 4
	D j	-2	-4
	х 3	5/3			-1/3
	х 2	1/3			1/3	10/3
	D j	-2/3			4/3	40/3
	х 1			3/5	-1/5	9/5
	х 2			-1/5	2/5	41/15
	D j			2/5	6/5	218/15

 

,

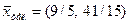Найдем дробные части чисел 9/5 и 41/15 (1 и 2 строки 3-го шага):

,

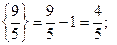
учитывая дробные части чисел 3/5 и -1/5 (1 строка 3-го шага):

,

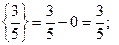
Составляем дополнительное ограничение целочисленности для 1-й строки 3-го шага: 3/5 х ₃ + 4/5 х ₄ ³ 4/5 или 3/5 х ₃ + 4/5 х ₄ - х ₅ ³ 4/5.

Дальнейшие расчеты проводим в табл. 17.2.

Таблица 17.2

ci	БП						bi
х 1	х 2	х 3	х 4	х 5
	х 1			3/5	-1/5		9/5
	х 2			-1/5	2/5		41/15
	D j			3/50	4/5	-1	4/5
	х 1				-1
	х 2				2/3	-1/3
	х 3				4/3	-5/3	4/3
	D j				2/3	2/3

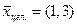при этом .

Сравнивая полученное значение целевой функции целочисленного решения со значением при оптимальном решении, следует заметить, что нахождение целочисленного решения приводит к уменьшению ее экстремального значения.

Ответ 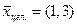,