Динамическое программирование связано с возможностью представления процесса управления в виде цепочки последовательных действий, или шагов, развернутых во времени и ведущих к цели. Таким образом, процесс управления можно разделить на части и представить его в виде динамической последовательности и интерпретировать в виде пошаговой программы, развернутой во времени. Это позволяет спланировать программу будущих действий. Поскольку вариантов возможных планов – программ множество, то необходимо из них выбрать лучший, оптимальный по какому-либо критерию в соответствии с поставленной целью.
Динамическое программирование (ДП) – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми. Начало развития ДП относится к 50-м годам ХХ в. Оно связано с именем американского математика Р.Э. Беллмана.
В реально функционирующих больших экономических системах еженедельно требуется принимать микроэкономические решения. Модели ДП позволяют на основе стандартного подхода принимать такие решения. Если каждое взятое в отдельности такое решение малосущественно, то в совокупности эти решения могут оказать большое влияние на прибыль.
Динамическое программирование (ДП) является одним из разделов оптимального программирования. Для него характерны специфические методы и приемы, применительные к операциям, в которых процесс принятия решения разбит на этапы (шаги). Методами ДП решаются вариантные оптимизационные задачи с заданными критериями оптимальности, с определенными связями между переменными и целевой функцией, выраженными системой уравнений или неравенств. При этом, как и в задачах, решаемых методами линейного программирования, ограничения могут быть даны в виде равенств или неравенств. Однако если в задачах линейного программирования зависимости между критериальной функцией и переменными обязательно линейны, то в задачах ДП эти зависимости могут иметь еще и нелинейный характер. ДП можно использовать как для решения задач, связанных с динамикой процесса или системы, так и для статических задач, связанных, например, с распределением ресурсов. Это значительно расширяет область применения ДП для решения задач управления. А возможность упрощения процесса решения, которая достигается за счет ограничения области и количества, исследуемых при переходе к очередному этапу вариантов, увеличивает достоинства этого комплекса методов.
Вместе с тем ДП свойственны и недостатки. Прежде всего, в нем нет единого универсального метода решения. Практически каждая задача, решаемая этим методом, характеризуется своими особенностями и требует проведения поиска наиболее приемлемой совокупности методов для ее решения. Кроме того, большие объемы и трудоемкость решения многошаговых задач, имеющих множество состояний, приводят к необходимости отбора задач малой размерности либо использования сжатой информации. Последнее достигается с помощью методов анализа вариантов и переработки списка состояний.
Для процессов с непрерывным временем ДП рассматривается как предельный вариант дискретной схемы решения. Получаемые при этом результаты практически совпадают с теми, которые получаются методами максимума Л. С. Понтрягина или Гамильтона-Якоби-Беллмана.
ДП применяется для решения задач, в которых поиск оптимума возможен при поэтапном подходе, например, распределение дефицитных капитальных вложений между новыми направлениями их использования; разработка правил управления спросом или запасами, устанавливающими момент пополнения запаса и размер пополняющего заказа; разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; составление календарных планов текущего и капитального ремонтов оборудования и его замены; поиск кратчайших расстояний на транспортной сети; формирование последовательности развития коммерческой операции и т.д.
Постановку задачи динамического программирования рассмотрим на примере инвестирования, связанного с распределением средств между предприятиями. В результате управления инвестициями система последовательно переводится из начального состояния S 0 в конечное Sn. Предположим, что управление можно разбить на n шагов и решение принимается последовательно на каждом шаге, а управление представляет собой совокупность n пошаговых управлений. На каждом шаге необходимо определить два типа переменных: переменную состояния системы Sk и переменную управления хk. Переменная Sk определяет, в каких состояниях может оказаться система на рассматриваемом k -м шаге. В зависимости от состояния S на этом шаге можно применить некоторые управления, которые характеризуются переменной хk, которые удовлетворяют определенным ограничениям и называются допустимыми.
Допустим, X = (x1, x2, …, xk, …, xn) – управление, переводящее систему из состояния S 0 в состояние Sn, a Sk – есть состояние системы на k -м шаге управления.
Применение управляющего воздействия хk на каждом шаге переводит систему в новое состояние S 1(S, хk) и приносит некоторый результат Wk (S, хk). Для каждого возможного состояния на каждом шаге среди всех возможных управлений выбирается оптимальное управление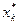 
, такое, чтобы результат, который достигается за шаги с k -го по последний n -й, оказался бы оптимальным. Числовая характеристика этого результата называется функцией Беллмана Fk (S) и зависит от номера шага k и состояния системы S.
Задача динамического программирования формулируется следующим образом: требуется определить такое управление Х*, переводящее систему из начального состояния S 0 в конечное состояние Sn, при котором целевая функция принимает наибольшее (наименьшее) значение
F (S 0, X*) → extr.
Особенности математической модели динамического программирования заключаются в следующем:
1) задача оптимизации формулируется как конечный многошаговый процесс управления;
2) целевая функция (выигрыш) является аддитивной и равна сумме целевых функций каждого шага:
;
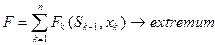3) выбор управления хk на каждом шаге зависит только от состояния системы к этому шагу Sk, и не влияет на предшествующие шаги (нет обратной связи);
4) состояние системы Sk после каждого шага управления зависит только от предшествующего состояния системы Sk -1 и этого управляющего воздействия хk (отсутствие последействия) и может быть записано в виде уравнения состояния: Sk = f (Sk -1, хk),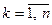 
;
5) на каждом шаге управление хk зависит от конечного числа управляющих переменных, а состояние системы Sk зависит от конечного числа параметров;
6) оптимальное управление представляет собой вектор X*, определяемый последовательностью оптимальных пошаговых управлений:
X* = (
, 
, …, , …, 
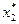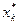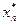), число которых и определяет количество шагов задачи.
