План.
16.1. Кооперативные игры.
16.2. Позиционные игры.
Кооперативные игры
Игроки могут выигрывать и проигрывать одновременно, их интересы могут не быть полностью противоположными, а поведение игроков становится более разнообразным. Такая ситуация весьма характерна для рыночных отношений.
В игре с ненулевой суммой становится желательным координировать свои действия с партнером либо каким-то образом влиять на его действия. Игры с ненулевой суммой могут быть кооперативными (в сообществе) и некооперативными (принятие решений независимо друг от друга).
В случае кооперативных игр важно определить точки равновесия игры. Понятие равновесия в теории игр шире понятия оптимизации включает последнее в качестве частного случая. В общем случае пара стратегий х* и у* для первого и второго игроков называется точкой равновесия по Нэшу, если обоим игрокам невыгодно отклоняться от своей стратегии в одиночку, т.е.
a 1 (x, у*) £ a 1 (х*, у*), a 1 (х*, у) £ a 1 (х*, у*) для любых х и у.
Пример. Определить точки равновесия для игры с матрицей выигрышей:
.
Решение. Нетрудно видеть, что в этой игре первому игроку невыгодно отклоняться от 1-й стратегии, если ее придерживается второй игрок, а второму игроку невыгодно отклоняться от 2-й стратегии, если ее придерживается первый игрок.
В теории игр доказано, что для любой конечной некооперативной игры с ненулевой суммой всегда существует по крайней мере одна равновесная пара смешанных стратегий; в общем случае равновесное решение может быть неединственным, причем каждому из них могут соответствовать разные значения выигрышей у игроков.
В случае кооперативной игры с двумя игроками предполагается, что игроки не могут воздействовать друг на друга до тех пор, пока не придут к некоторому соглашению.
В этом случае игра (вернее ее исходы) представляется, как множество S на плоскости общих выигрышей а 1 и а 2 (рис. 16.1). Задаются значения выигрышей Т1 и Т2, которые могут получить соответственно 1-й и 2-й игроки без кооперации с партнером. В предположении о том, что множество S является выпуклым, замкнутым и ограниченным сверху, можно доказать, что оптимальные решения находятся на правой верхней границе этого множества.
На этой границе выделяется множество Р парето-оптимальных решений, на котором увеличение выигрыша одного из игроков возможно только за счет уменьшения выигрыша его партнера. На множестве Р точками 
и 
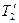ограничено переговорное множество N; оно характерно тем, что игрокам нет смысла вести переговоры относительно решений вне его, так как положение одного из игроков может быть либо улучшено без ущерба для партнера, либо он может достичь лучшего выигрыша в одиночку. На переговорном множестве выделяется точка N *, соответствующая равновесию по Нэшу – точка Нэша; в ней достигается максимум произведения
max(a 1 – T 1)(a 2 – T 2),
в котором сомножители представляют собой превышения выигрышей каждого из игроков над платежами, которые могут быть получены игроками без кооперации.
Рис. 16.1.
Точка Нэша является одним из возможных решений кооперативной игры, наиболее привлекательных для партнеров.
Пример. Кооперативная игра дается матрицей выигрышей:
.
Определить основные характеристики игры.
Решение. На плоскости а 10 а 2 множеством S, определяющим игру, является треугольник с вершинами, данными в матрице: 0 (0, 0), А(2, 8), В(8, 2); это множество является выпуклым (рис. 16.2).
Рис. 16.2
Сторона АВ треугольника представляет собой парето-оптимальное множество: увеличение выигрыша одного игрока возможно только за счет партнера. Точка Т (4, 4) определяет выигрыши, которые игроки могут получить без взаимодействия с партнером. Переговорное множество N (отрезок и 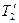) лежит на линии АВ. На этой линии находится точка Нэша N*(5, 5) – в ней произведение (a 1 – 5)(a 2 – 5) для точек max(a 1, a 2), лежащих вне множества N, принимает наибольшее значение.
Позиционные игры
Игры, в которых задается последовательность принятия решений игроками, называются позиционными играми. Число игроков в них может изменяться от двух и более. Игрок принимает решение, зная о решении партнера (соперника), т.е. в ответ на его решение. К позиционным многошаговым играм двух лиц, где игроки принимают свои решения, зная обо всех предыдущих решениях партнера, относятся, например, шахматы и шашки.
Позиционная игра может быть представлена в виде дерева решений (в общем виде – графа решений). Вершины дерева игры называются позициями. Позиции, непосредственно следующие за некоторой позицией, – это альтернативы; позиции, не имеющие альтернатив, называются окончательными, а ведущие в них пути – партиями. Часть дерева решений, описывающая игру из некоторой позиции (которая может считаться начальной), называют подыгрой. Всю игру можно разбить на ряд подыгр, и решения из них представляют собой самостоятельные задачи. Примером подыгры являются шахматные этюды.
Пример игры «Вступление на рынок».
Пусть на рынке доминирует производитель – фирма 1 и монопольное положение приносит ей прибыль 10 млн ден. ед. Фирма 2 решает вопрос о внедрении на этот рынок при следующих известных предпосылках.
В случае вступления фирмы 2 на рынок фирма 1 может отреагировать следующим образом:
а) снизить объем производства и тогда поделить с фирмой 2 свою прибыль по 5 млн ден. ед. на каждого конкурента;
б) не уступать в объеме производства – тогда прибыль фирмы 1 понизится до 3 млн ден. ед. вследствие снижения рыночной цены, а фирма 2 понесет убытки в размере 2 млн ден. ед. тоже из-за падения рыночной цены на товар, а также из-за того, что предварительные затраты на проработку рынка и организацию производства не будут компенсированы.
Если фирма 2 воздерживается от вступления на рынок, то она ничего не выигрывает и не проигрывает, т.е. ее прибыль будет нулевой. В этом случае за фирмой 1 по-прежнему остаются два варианта поведения: не снижать объем производства с прибылью 10 млн ден. ед. и снизить объем производства со снижением прибыли до 8 млн ден. ед.
Эта конечная неантагонистическая игра двух партнеров может быть описана матрицей выигрышей:
| Стратегия фирмы 1 | |||
| сохранить объем производства | снизить объем производства | ||
| Стратегия фирмы 2 | вступить | (3; -2) | (5; 5) |
| не вступить | (10; 0) | (8; 0) |
Вместе с тем, эту игру можно представить также деревом решений, ветви которого соответствуют решениям партнеров, а выигрыши игроков указаны около каждой из висячих вершин (рис. 16.3).
Рассматриваемая игра имеет две пары стратегий (две партии), приводящих к равновесию по Нэшу; при отказе фирмы 2 от внедрения на рынок фирма 1 не меняет объем производства; в случае вступления фирмы 2 на рынок фирма 1 снижает объем производства.
В непозиционной игре, когда игроки принимают решения одновременно и независимо друг от друга, реализация обеих стратегий была бы равновероятна. В позиционной игре необходимо учитывать, что фирма 1 принимает свои решения, уже зная о решении фирмы 2. Согласно принципу максимина, фирме 2 следовало бы избрать стратегию отказа от вступления на рынок: в этом случае ее прибыль составит 0 млн ден. ед., а это больше, чем – 2 млн ден. ед. в случае вступления. Однако здесь не учитывается предположение о рациональном поведении игроков, основой которого является стремление к максимизации своих выигрышей – в данном случае прибыли.
Рисунок – 16.3
С учетом этого обстоятельства более рациональной стратегией фирмы 1 при вступлении фирмы 2 на рынок является снижение производства, так как прибыль 5 млн ден. ед. все-таки больше, чем прибыль 3 млн ден. ед. Именно эта партия наиболее вероятна для реализации, когда фирма 2 вступит на рынок.
Приведенный пример описывает случай так называемой неустойчивой монополии, когда фирма-монополист не в состоянии эффективно противостоять внедрению конкурента на рынок.
Однако возможен вариант устойчивой монополии, когда фирма-монополист в силу условий организации своего производства в состоянии эффективно реализовывать подавление потенциальных соперников на рынке.
