Рассмотрим пример (игра со спичками). Пусть на столе лежат 30 спичек. Каждый игрок может взять 1, 2 или 3 спички. Проигравшим считается тот, кто взял последнюю спичку. Может ли первый игрок всегда добиться выигрыша?
Решение. Очевидно, что тот игрок, перед ходом которого на столе осталась только одна спичка, проигрывает. Если на столе останется 5 спичек, то тот, кто делает ход, проигрывает. Это следует из того, что какой бы он ход ни сделал, другой игрок всегда может совершить такой ход, после которого на столе останется 1 спичка.
Действительно, если, например, на столе останется 5 спичек и очередным ходом забираются 2 спички, то следующий игрок забирает две спички и он выиграл. Рассуждая аналогичным образом, логично прийти к заключению, что тот игрок, перед ходом которого на столе остается 5, 9, 13, 17, 21, 25 или 29 спичек, проигрывает при правильной игре его противника. Таким, образом, первый игрок всегда может выиграть, взяв со стола на первом ходу одну спичку и тем самым оставив на столе 29 спичек. Следует обратить внимание, что схема решения этой задачи заключалась в движении от конца к началу.
Такая схема решения опирается на принцип оптимальности, сформулированный американским математиком Р.Э. Беллманом в 1953 г.: каково бы ни было состояние s системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Данный принцип верен при условии, что процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияние на предшествующие шаги.
Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом.
При решении задачи на каждом шаге выбирается управление, которое должно привести к оптимальному выигрышу. Если считать все шаги независимыми, тогда оптимальным управлением будет то управление, которое обеспечит максимальный выигрыш именно на данном шаге. Однако, например, при покупке новой техники взамен устаревшей на ее приобретение затрачиваются определенные средства, поэтому доход от ее эксплуатации в начале может быть небольшой, а в следующие годы новая техника будет приносить больший доход. И наоборот, если принято решение оставить старую технику для получения дохода в текущем году, то в дальнейшем это приведет к значительным убыткам. Этот пример демонстрирует следующий факт: в многошаговых процессах управление на каждом конкретном шаге надо выбирать с учетом его будущих воздействий на весь процесс.
Кроме того, при выборе управления на данном шаге следует учитывать возможные варианты состояния предыдущего шага. Например, при определении количества средств, вкладываемых в предприятие в 1-м году, необходимо знать, сколько средств осталось в наличии к этому году и какой доход получен в предыдущем (i -1)-м году. Таким образом, при выборе шагового управления необходимо учитывать следующие требования:
1) возможные исходы предыдущего шага Sk -1;
2) влияние управления хk на все оставшиеся до конца процесса шаги (n - k).
В задачах динамического программирования первое требование учитывают, делая на каждом шаге условные предположения о возможных вариантах окончания предыдущего шага и проводя для каждого из вариантов условную оптимизацию. Выполнение второго требования обеспечивается тем, что в этих задачах условная оптимизация проводится от конца процесса к началу.
Условная оптимизация. На первом этапе решения задачи, называемом условной оптимизацией, определяются функция Беллмана и оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего в соответствии с алгоритмом обратной прогонки. На последнем, n-м шаге, оптимальное управление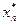 
определяется функцией Беллмана:
F (S) = max{ Wn (S, x n)},
в соответствии с которой максимум выбирается из всех возможных значений хn, причем х nÎХ.
Дальнейшие вычисления производятся согласно рекуррентному соотношению, связывающему функцию Беллмана на каждом шаге с этой же функцией, но вычисленной на предыдущем шаге. В общем виде это уравнение имеет вид:
Fn (S) = max{ Wn (S, x n) + Fk +1(S 1(S, x k))}, x kÎХ.
Этот максимум (или минимум) определяется по всем возможным для k и S значениям переменной управления X.
Безусловная оптимизация. После того, как функция Беллмана и соответствующие оптимальные управления найдены для всех шагов с n -го по первый, осуществляется второй этап решения задачи, называемый безусловной оптимизацией. Пользуясь тем, что на первом шаге (k = 1) состояние системы известно – это ее начальное состояние S 0, можно найти оптимальный результат за все n шагов и оптимальное управление на первом шаге x 1, которое этот результат доставляет. После применения этого управления система перейдет в другое состояние S 1(S, 
), зная которое, можно, пользуясь результатами условной оптимизации, найти оптимальное управление на втором шаге , и так далее до последнего n-го шага.
Вычислительную схему динамического программирования можно строить на сетевых моделях, а также по алгоритмам прямой прогонки (от начала) и обратной прогонки (от конца к началу). Рассмотрим примеры решения различных по своей природе задач, содержание которых требует выбора переменных состояния и управления.
