План.
14.1. Связь матричных игр и линейного программирования.
14.2. Алгоритм решения матричных игр с помощью линейного программирования.
Связь матричных игр и линейного программирования
Теория игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования. Г Данциг указывает, что создатель теории игр Дж. Фон Нейман, который первым ввел симплекс-метод в линейное программирование (1947 г.), установил это соотношение и в дальнейшем обосновал и развил концепцию двойственности в линейном программировании.
Допустим, дана игра двух лиц, заданная платежной матрицей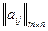 
. Тогда оптимальная смешанная стратегия первого игрока определяется условиями
, 
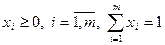. (14.1)
Эта задача может быть сформулирована в виде задачи линейного программирования. Пусть
.
Тогда может быть составлена математическая модель задачи для первого игрока. Исходя из чистых стратегий второго игрока целевая функция игры:
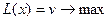(14.2)
при ограничениях
.
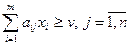
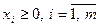Для второго игрока задача записывается в виде
, 
.
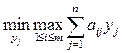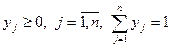Промежуточное соотношение:
.
Тогда задача примет вид
(14.3)
при ограничениях
.
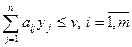
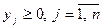Задача для второго игрока (14.3) является двойственной к задаче для первого игрока (14.2). Задача для второго игрока может быть решена, например, стандартным симплекс-методом, а для первого игрока – двойственным симплекс-методом. Выбор метода определяется тем, какая из задач имеет меньше ограничений, что в свою очередь зависит от числа чистых стратегий каждого из игроков.
Математическую модель задачи (14.2) можно упростить, разделив все (n + 1) ограничения на v. Это возможно при v ¹ 0. При v = 0 рекомендуется прибавить любое положительное число ко всем элементам платежной матрицы, что гарантирует положительность значения модифицированной игры. Действительное значение игры получается вычитанием из модифицированного значения этого положительного числа. Если v < 0, то надо сменить знаки неравенств.
Полагая v > 0, систему ограничений можно записать:
.
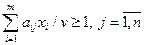
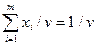Полагая Xi = xi / v и если v ® max, то 1/ v ® min, получим задачу линейного программирования вида
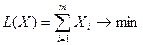
при ограничениях
.
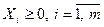Аналогично, исходя из чистых стратегий первого игрока или по правилам составления двойственных задач, принимая математическую модель первого игрока как исходную, математическая модель второго игрока записывается в виде
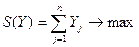
при ограничениях
,
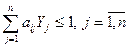
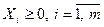где S (Y) max = L (X) min = 1/ v, Yj = yj / n.
