10. Скласти рівняння сторін і медіан трикутника з вершинами  ,
, 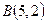 ,
,  .
.
11. Скласти рівняння кола, що проходить через три дані точки:  ,
, 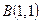 ,
,  .
.
12. Побудувати лінії, які задані рівняннями.
а)  б)
б)  в)
в) 
Варіант №15.
Контрольна робота №1:
«Елементи лінійної алгебри й аналітичної геометрії»
Тема 1: Лінійна алгебра.
1. Обчислити визначники: 1) 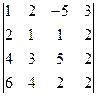 2)
2) 
2. Обчислити обернену матрицю до матриці  . Перевірити правильність обчислень, використовуючи означення оберненої матриці.
. Перевірити правильність обчислень, використовуючи означення оберненої матриці. 
3. Обчислити ранг матриці. 
4. Розв’язати системи лінійних алгебраїчних рівнянь: методом Крамера, методом Гауса і засобами матричного обчислення (там, де це можливо):
а)  б)
б)  в)
в) 
5. Дослідити на сумісність СЛАР і, у випадку позитивної відповіді, знайти її розв’язок.

Тема 2: Векторна алгебра.
6. Написати розвиненя вектора  за векторами
за векторами  ,
,  і
і  .
.
 ,
,  ,
,  ,
,  ,
,
7. Чи колінеарні вектори 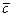 і
і  , побудовані на векторах
, побудовані на векторах  і
і  ?
?
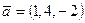 ,
,  ,
,  ,
, 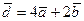
8. Знайти косинус кута між векторами 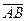 і
і  .
.
 ,
,  ,
, 
9. Задані координати вершин 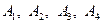 піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра
піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра  ; 2) кут між ребрами
; 2) кут між ребрами  и
и  ; 3) площу грані
; 3) площу грані  ; 4) об’єм піраміди
; 4) об’єм піраміди 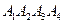 .
. 
Тема 3: Аналітична геометрія.
10. Через точки  і
і  проведена пряма. Визначити точки перетину цієї прямої з осями координат.
проведена пряма. Визначити точки перетину цієї прямої з осями координат.
11. Скласти рівняння гіперболи, осі симетрії якої збігаються з осями координат, якщо дана точка перетину  однієї з асимптот з однією з директрис цієї гіперболи.
однієї з асимптот з однією з директрис цієї гіперболи.
12. Побудувати лінії, які задані рівняннями.
а) 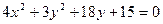 б)
б)  в)
в) 
Варіант №16.
Контрольна робота №1:
«Елементи лінійної алгебри й аналітичної геометрії»
Тема 1: Лінійна алгебра.
1. Обчислити визначники: 1) 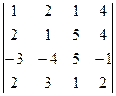 2)
2) 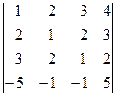
2. Обчислити обернену матрицю до матриці  . Перевірити правильність обчислень, використовуючи означення оберненої матриці.
. Перевірити правильність обчислень, використовуючи означення оберненої матриці. 
3. Обчислити ранг матриці. 
4. Розв’язати системи лінійних алгебраїчних рівнянь: методом Крамера, методом Гауса і засобами матричного обчислення (там, де це можливо):
а)  б)
б) 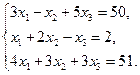 в)
в) 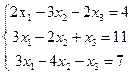
5. Знайти множину розв’язків однорідної системи 3-х лінійних рівнянь з чотирма невідомими

Тема 2: Векторна алгебра.
6. Написати розвиненя вектора  за векторами
за векторами  ,
,  і
і  .
.
 ,
, 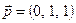 ,
,  ,
,  ,
,
7. Обчислити площу паралелограма, побудованого на векторах  і
і  ,якщо кут між векторами
,якщо кут між векторами  і
і  дорівнює
дорівнює  .
.  ,
,  ,
,  ,
, 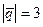 ,
, 
8. Чи компланарні вектори  ,
,  і
і 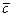 ?
?
 ,
,  ,
, 
9. Задані координати вершин 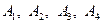 піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра
піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра  ; 2) кут між ребрами
; 2) кут між ребрами  и
и  ; 3) площу грані
; 3) площу грані  ; 4) об’єм піраміди
; 4) об’єм піраміди 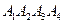 .
.  .
.
Тема 3: Аналітична геометрія.
10. Визначити, приякому значенні 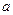 три прямі
три прямі 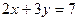 ,
,  і
і  будуть перетинатися в одній точці.
будуть перетинатися в одній точці.
11. Провести до еліпса 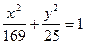 дотичні перпендикулярні до прямої
дотичні перпендикулярні до прямої  .
.
12. Побудувати лінії, які задані рівняннями.
а)  б)
б)  в)
в) 
Варіант №17.
Контрольна робота №1:
«Елементи лінійної алгебри й аналітичної геометрії»
Тема 1: Лінійна алгебра.
1. Обчислити визначники: 1)  2)
2) 
2. Обчислити обернену матрицю до матриці  . Перевірити правильність обчислень, використовуючи означення оберненої матриці.
. Перевірити правильність обчислень, використовуючи означення оберненої матриці. 
3. Обчислити ранг матриці. 
4. Розв’язати системи лінійних алгебраїчних рівнянь: методом Крамера, методом Гауса і засобами матричного обчислення (там, де це можливо):
а)  б)
б)  в)
в) 
5. Дослідити на сумісність СЛАР і, у випадку позитивної відповіді, знайти її розв’язок
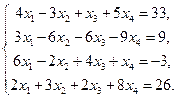
Тема 2: Векторна алгебра.
6. Написати розвиненя вектора  за векторами
за векторами  ,
,  і
і  .
.
 ,
,  ,
,  ,
,  ,
,
7. Чи колінеарні вектори 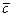 і
і  , побудовані на векторах
, побудовані на векторах  і
і  ?
?
 ,
,  ,
,  ,
, 
8. Знайти косинус кута між векторами 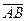 і
і  .
.
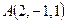 ,
,  ,
, 
9. Задані координати вершин 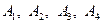 піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра
піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра  ; 2) кут між ребрами
; 2) кут між ребрами  и
и  ; 3) площу грані
; 3) площу грані  ; 4) об’єм піраміди
; 4) об’єм піраміди 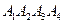 .
. 






