10. Задані координати кінців відрізка  і
і  . Скласти рівняння прямих, що проходять через точку
. Скласти рівняння прямих, що проходять через точку 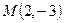 паралельно і перпендикулярно до відрізка
паралельно і перпендикулярно до відрізка 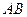 .
.
11. Знайти рівняння траєкторії точки  , що рухається так, що відстань від точки
, що рухається так, що відстань від точки  залишається вдвічі меншою відстані від прямої.
залишається вдвічі меншою відстані від прямої.
12. Побудувати лінії, які задані рівняннями.
а)  б)
б)  в)
в) 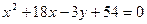
Варіант №5.
Контрольна робота №1:
«Елементи лінійної алгебри й аналітичної геометрії»
Тема 1: Лінійна алгебра.
1. Обчислити визначники: 1) 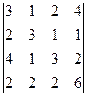 2)
2) 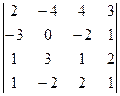
2. Обчислити обернену матрицю до матриці  . Перевірити правильність обчислень, використовуючи означення оберненої матриці.
. Перевірити правильність обчислень, використовуючи означення оберненої матриці. 
3. Обчислити ранг матриці. 
4. Розв’язати системи лінійних алгебраїчних рівнянь: методом Крамера, методом Гауса і засобами матричного обчислення (там, де це можливо):
а) 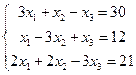 б)
б)  в)
в) 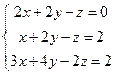
5. Дослідити на сумісність СЛАР і, у випадку позитивної відповіді, знайти її розв’язок.
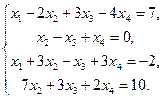
Тема 2: Векторна алгебра.
6. Написати розвиненя вектора  за векторами
за векторами  ,
,  і
і  .
.
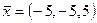 ,
, 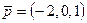 ,
, 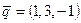 ,
, 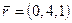
7. Чи колінеарні вектори 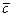 і
і  , побудовані на векторах
, побудовані на векторах  і
і  ?
?
 ,
,  ,
, 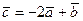 ,
, 
8. Знайти косинус кута між векторами 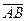 і
і  .
.
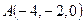 ,
, 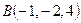 ,
, 
9. Задані координати вершин 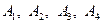 піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра
піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра  ; 2) кут між ребрами
; 2) кут між ребрами  и
и  ; 3) площу грані
; 3) площу грані  ; 4) об’єм піраміди
; 4) об’єм піраміди 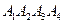 .
.  .
.
Тема 3: Аналітична геометрія.
10. Задані вершини трикутника 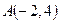 ,
, 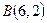 і
і  . Скласти рівняння висоти і медіани, проведених з вершини
. Скласти рівняння висоти і медіани, проведених з вершини  .
.
11. Фокуси гіперболи знаходяться в точках 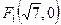 і
і 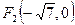 . Гіпербола проходить через точку
. Гіпербола проходить через точку 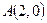 . Знайти рівняння її асимптот і кут між ними.
. Знайти рівняння її асимптот і кут між ними.
12. Побудувати лінії, які задані рівняннями.
а)  б)
б)  в)
в) 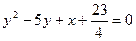
Варіант №6.
Контрольна робота №1:
«Елементи лінійної алгебри й аналітичної геометрії»
Тема 1: Лінійна алгебра.
1. Обчислити визначники: 1)  2)
2) 
2. Обчислити обернену матрицю до матриці  . Перевірити правильність обчислень, використовуючи означення оберненої матриці.
. Перевірити правильність обчислень, використовуючи означення оберненої матриці. 
3. Обчислити ранг матриці. 
4. Розв’язати системи лінійних алгебраїчних рівнянь: методом Крамера, методом Гауса і засобами матричного обчислення (там, де це можливо):
а) 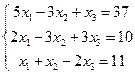 б)
б) 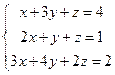 в)
в) 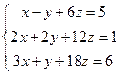
5. Знайти множину розв’язків однорідної системи 3-х лінійних рівнянь з чотирма невідомими.
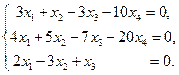
Тема 2: Векторна алгебра.
6. Написати розвиненя вектора  за векторами
за векторами  ,
,  і
і  .
.
 ,
, 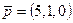 ,
,  ,
, 
7. Обчислити площу паралелограма, побудованого на векторах  і
і  ,якщо кут між векторами
,якщо кут між векторами  і
і  дорівнює
дорівнює  .
. 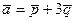 ,
,  ,
,  ,
, 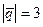 ,
, 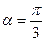
8. Чи компланарні вектори  ,
,  і
і 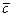 ?
?
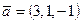 ,
, 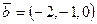 ,
, 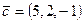
9. Задані координати вершин 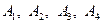 піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра
піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра  ; 2) кут між ребрами
; 2) кут між ребрами  и
и  ; 3) площу грані
; 3) площу грані  ; 4) об’єм піраміди
; 4) об’єм піраміди 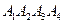 .
.  .
.
Тема 3: Аналітична геометрія.
10. Задані рівняння 3-х сторін трикутника 
 ,
, 
 і
і 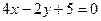
 . Скласти рівняння висоти
. Скласти рівняння висоти 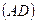 .
.
11. На гіперболі 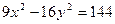 знайти точку, відстань якої від лівого фокуса вдвічі менша, ніж від правого.
знайти точку, відстань якої від лівого фокуса вдвічі менша, ніж від правого.
12. Побудувати лінії, які задані рівняннями.
а) 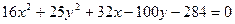 б)
б)  в)
в) 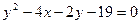
Варіант №7.
Контрольна робота №1:
«Елементи лінійної алгебри й аналітичної геометрії»
Тема 1: Лінійна алгебра.
1. Обчислити визначники: 1)  2)
2) 
2. Обчислити обернену матрицю до матриці  . Перевірити правильність обчислень, використовуючи означення оберненої матриці.
. Перевірити правильність обчислень, використовуючи означення оберненої матриці. 
3. Обчислити ранг матриці. 
4. Розв’язати системи лінійних алгебраїчних рівнянь: методом Крамера, методом Гауса і засобами матричного обчислення (там, де це можливо):
а)  б)
б) 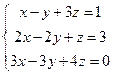 в)
в) 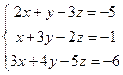
5. Дослідити на сумісність СЛАР і, у випадку позитивної відповіді, знайти її розв’язок.
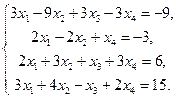
Тема 2: Векторна алгебра.
6. Написати розвиненя вектора  за векторами
за векторами  ,
,  і
і  .
.
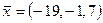 ,
, 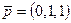 ,
, 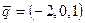 ,
, 
7. Чи колінеарні вектори 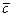 і
і  , побудовані на векторах
, побудовані на векторах  і
і  ?
?
 ,
, 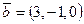 ,
, 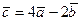 ,
, 
8. Знайти косинус кута між векторами 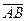 і
і  .
.
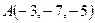 ,
, 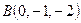 ,
, 
9. Задані координати вершин 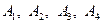 піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра
піраміди. За допомоги векторної алгебри знайти: 1) довжину ребра  ; 2) кут між ребрами
; 2) кут між ребрами  и
и  ; 3) площу грані
; 3) площу грані  ; 4) об’єм піраміди
; 4) об’єм піраміди 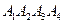 .
. 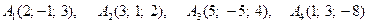 .
.




