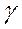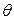1) Основные понятия
Поверхность в пространстве, как правило можно рассматривать как геометрическое место точек удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в т.О1.есть геометрическое место точек удаленных от т. О1 на расстояние R. Прямоугольная система координат Oxyz позволяет однозначно установить соответствие между точками пространства и тройками чисел x,y,z- их координатами. Свойства, общие всем точкам, можно записать в виде уравнения, связывающего координаты всех точек поверхности. Уравнение данной поверхности в прямоугольной системе координат Oxyz называют уравнением вида F(x,y,z)=0, с тремя переменными x,y,z которому удовлетворяют координаты каждой точки лежащей на поверхности и не удовлетворяют координаты точек не лежащие на поверхности.
2) Уравнение линии в пространстве
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей или как геометрическое место точек общих двум поверхностям. Если F1(x,y,z)=0 и F2(x,y,z) уравнения двух поверхностей, то координаты линии их пересечения (L) должно удовлетворять системе двух уравнений с тремя неизвестными

 -это уравнение линии в пространстве.
-это уравнение линии в пространстве.
Линию в пространстве можно рассматривать и как траекторию движения точки. В этом случае ее задают векторным уравнением r=r(t) или параметрическим уравнениями.
 -проекции вектора r на оси координат.
-проекции вектора r на оси координат.
3) Уравнение прямой в пространстве
1. Векторное уравнение прямой
Положение прямой в пространстве вполне определено, если задать какую-либо точку M0 на прямой и вектор  параллельный этой прямой. Вектор
параллельный этой прямой. Вектор  - называется направляющим вектором прямой. Пусть прямая L задана ее точкой M0(x0,y0,z0) и направляющим вектором
- называется направляющим вектором прямой. Пусть прямая L задана ее точкой M0(x0,y0,z0) и направляющим вектором  (m,n,p). Возьмем на прямой L произвольную точку M(x,y,z). Обозначим радиус –
(m,n,p). Возьмем на прямой L произвольную точку M(x,y,z). Обозначим радиус –
|

|
|
|
|
|
|
|
|





 векторы точек M0 и M соответственно через
векторы точек M0 и M соответственно через  и
и  . Очевидно, что
. Очевидно, что  =
=  +
+  . Вектор
. Вектор  М, лежащий на прямой L параллелен направляющему вектору
М, лежащий на прямой L параллелен направляющему вектору  , поэтому
, поэтому  M=t
M=t  , где t- скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки M на прямой (рис.1.). Тогда уравнение можно записать в виде
, где t- скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки M на прямой (рис.1.). Тогда уравнение можно записать в виде  =
=  +t
+t  - векторное уравнение прямой.
- векторное уравнение прямой.
2. Параметрическое уравнение прямой
Поскольку  =(x,y,z),
=(x,y,z),  =(x0,y0,z0), t
=(x0,y0,z0), t  =(tm,tn,tp), то уравнение прямой можно записать в виде:
=(tm,tn,tp), то уравнение прямой можно записать в виде:
 . Отсюда
. Отсюда  - параметрическое уравнение прямой в пространстве.
- параметрическое уравнение прямой в пространстве.
|
исключая из параметрического уравнения прямой t получим:

 - каноническое уравнение прямой.
- каноническое уравнение прямой.
4. Уравнение прямой проходящей через две точки
Пусть прямая L проходит через точки M1(x1,y1,z1) и M2(x2,y2,z2). В качестве направляющего вектора  можно взять
можно взять  , т.е.
, т.е.  =
=  , следовательно, m=x2-x1, n=y2-y1, p=z2-z1. поскольку наша прямая проходит через т.M1(x,y,z) то каноническое уравнение примет вид:
, следовательно, m=x2-x1, n=y2-y1, p=z2-z1. поскольку наша прямая проходит через т.M1(x,y,z) то каноническое уравнение примет вид:

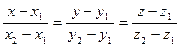 - уравнение прямой проходящей через две точки.
- уравнение прямой проходящей через две точки.
5. Угол между прямыми
Пусть L1 и L2 заданы уравнениями

 . Под углом между этими прямыми понимают угол между направляющими векторами
. Под углом между этими прямыми понимают угол между направляющими векторами  1(m1,n1,p1) и
1(m1,n1,p1) и  2(m2,n2,p2).Поэтому по известной формуле для косинуса угла между векторами получим
2(m2,n2,p2).Поэтому по известной формуле для косинуса угла между векторами получим 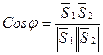 или
или

Если L1 перпендикулярна L2, то в этом случае cosφ=0, следовательно

Если L1 || L2, то векторы  1 ||
1 ||  2 и координаты векторов
2 и координаты векторов  1 и
1 и  2 пропорциональны:
2 пропорциональны:
 .
.
4) Уравнение плоскости в пространстве.
Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать различными способами и каждому из них соответствует конкретное уравнение.
1. Уравнение плоскости проходящей через точку перпендикулярно вектору.
Пусть в пространстве Oxyz плоскость Q задана точкой M0(x0,y0,z0) и вектором 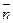 =(A,B,C) перпендикулярным этой плоскости. Возьмем на плоскости произвольную точку M(x,y,z) и составим вектор
=(A,B,C) перпендикулярным этой плоскости. Возьмем на плоскости произвольную точку M(x,y,z) и составим вектор  . Так как
. Так как  перпендикулярен Q, то вектор
перпендикулярен Q, то вектор 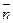 перпендикулярен вектору
перпендикулярен вектору  , поэтому их скалярное произведение
, поэтому их скалярное произведение 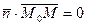 , т.е.
, т.е.

 (1)
(1)
-это уравнение плоскости проходящей через данную точку перпендикулярную вектору 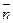 . Вектор n=(A,B,C) называется нормальным вектором плоскости. Придавая коэффициентам A,B,C различные значения можно получить уравнения любых плоскостей проходящих через т.M0.
. Вектор n=(A,B,C) называется нормальным вектором плоскости. Придавая коэффициентам A,B,C различные значения можно получить уравнения любых плоскостей проходящих через т.M0.
2. Общее уравнение плоскости
Рассмотрим общее уравнение первой степени с тремя переменными x,y и z.
 (2)
(2)
Полагая, что по крайней мере, один из коэффициентов A,B или C≠0, например B≠0, перепишем его в виде:

Сравнивая полученное уравнение с ранее полученным (1) видим, что последнее является уравнением плоскости с нормальным вектором 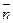 =(A,B,C), проходящее через точку
=(A,B,C), проходящее через точку  . Итак уравнение (2) определяет в пространстве Oxyz некоторую плоскость. Это уравнение и называется общим уравнением плоскости.
. Итак уравнение (2) определяет в пространстве Oxyz некоторую плоскость. Это уравнение и называется общим уравнением плоскости.
Частные случаи:
а) Если D=0, то  . Этому уравнению отвечает т.O(0,0,0)-начало координат. Следовательно, эта плоскость проходит через начало координат;
. Этому уравнению отвечает т.O(0,0,0)-начало координат. Следовательно, эта плоскость проходит через начало координат;
б) Если C=0, имеем  , вектор
, вектор 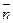 (A,B,0) перпендикулярен оси Oz. Следовательно, плоскость параллельна Oz; B=0, то || оси Oy; A=0, то || оси Ox.
(A,B,0) перпендикулярен оси Oz. Следовательно, плоскость параллельна Oz; B=0, то || оси Oy; A=0, то || оси Ox.
в) Если C=D=0, то плоскость проходит через т.O(0,0,0) и || Oz, то есть проходит через ось Oz;
г) Если A=B=0, то Cz+D=0, то есть Z=  , плоскость || плоскости Oxy;
, плоскость || плоскости Oxy;
д) Если A=B=D=0, то Cz=0, то есть Z=0, это уравнение плоскости Oxy.
3. Уравнение плоскости, проходящей через три точки.
Три точки в пространстве не лежащие на одной прямой определяют единственную плоскость. Найдем уравнение плоскости Q,проходящей через три данных точки M1(x1,y1,z1), M2(x2,y2,z2) и M3(x3,y3,z3), не лежащие на одной прямой. Возьмем на плоскости произвольную точку M(x,y,z) и составим векторы  ;
;  и
и  . Эти векторы компланарны. Используя условия компланарности трех векторов (их смешанное произведение=0) получим:
. Эти векторы компланарны. Используя условия компланарности трех векторов (их смешанное произведение=0) получим:

 т.е.
т.е.
 (1)
(1)
-это уравнение есть уравнение плоскости, проходящей через три точки.
4. Уравнение плоскости в отрезках
Пусть плоскость отсекает на осях Ox, Oy и Oz соответственно отрезки  ,b,c. То есть она проходит через три точки A(
,b,c. То есть она проходит через три точки A( ,0,0),B(0,b0) и C(0,0,c). Подставляя в уравнение (1) получим:
,0,0),B(0,b0) и C(0,0,c). Подставляя в уравнение (1) получим:

 =0. Раскрыв определитель имеем:
=0. Раскрыв определитель имеем:
 или
или  -уравнение плоскости в отрезках на осях.
-уравнение плоскости в отрезках на осях.
5. Нормальное уравнение плоскости
Положение плоскости Q можно определить заданием единичного вектора  , совпадающего с направлением OK – перпендикуляром, опущенным из начала координат на плоскость и длинной этого перпендикуляра (рис.2)
, совпадающего с направлением OK – перпендикуляром, опущенным из начала координат на плоскость и длинной этого перпендикуляра (рис.2)
|
|
|
|
|
|
|
|
|










 Пусть OK=P, а α, β и γ-углы, образованные вектором
Пусть OK=P, а α, β и γ-углы, образованные вектором  с осями Ox, Oy и Oz. Тогда
с осями Ox, Oy и Oz. Тогда  =
= 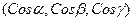 . Возьмем на плоскости произвольную точку M(x,y,z) и соединим ее с началом координат. Образуем вектор
. Возьмем на плоскости произвольную точку M(x,y,z) и соединим ее с началом координат. Образуем вектор =
=  =(x,y,z). При любом положении
=(x,y,z). При любом положении
точки M на плоскости Q проекция вектора  на направление вектора
на направление вектора  всегда равно p.
всегда равно p.

 т.е.
т.е. 
 или
или 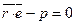 - это нормальное уравнение плоскости. Зная координаты r и e можно его переписать в следующей форме:
- это нормальное уравнение плоскости. Зная координаты r и e можно его переписать в следующей форме:

6. Угол между двумя плоскостями
пусть заданы две плоскости Q1 и Q2:

Под углом между плоскостями понимают один из двугранных углов образованных этими плоскостями. Угол φ между нормальными векторами  (A1,B1,C1) и
(A1,B1,C1) и  (A2,B2,C2) плоскостей Q1 Q2 равен одному из этих углов. Поэтому
(A2,B2,C2) плоскостей Q1 Q2 равен одному из этих углов. Поэтому  или
или 
 . Для нахождения острого угла следует взять модуль правой части. Если Q1 перпендикулярнa Q2, то вектор
. Для нахождения острого угла следует взять модуль правой части. Если Q1 перпендикулярнa Q2, то вектор  перпендикулярен вектору
перпендикулярен вектору  , тогда вектор
, тогда вектор  =0, то есть
=0, то есть  .
.
полученное равенство есть условие перпендикулярности Q1 и Q2. Если Q1 || Q2, то  ||
||  , тогда координаты векторов пропорциональны, то есть
, тогда координаты векторов пропорциональны, то есть  - это условие параллельности Q1 и Q2.
- это условие параллельности Q1 и Q2.
7. Расстояние от точки до плоскости.
|
 (Pис.3) Найдем d- расстояние от точки до плоскости. Расстояние d от точки M0 до плоскости Q равно модулю проекции вектора M1M0 (Рис.3), где M1(x1,y1,z1)- произвольная точка плоскости Q на направление нормального вектора
(Pис.3) Найдем d- расстояние от точки до плоскости. Расстояние d от точки M0 до плоскости Q равно модулю проекции вектора M1M0 (Рис.3), где M1(x1,y1,z1)- произвольная точка плоскости Q на направление нормального вектора  =(A,B,C). Следовательно
=(A,B,C). Следовательно 
 =
=
|
|
|




 =
= 
|





Так как т.M1 принадлежит Q, то
|
|



 ,и
,и 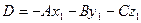 , тогда уравнение примет вид:
, тогда уравнение примет вид:
|
 .
.
8 .Угол между прямой и плоскостью
Пусть плоскость задана уравнением 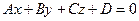 , а прямая L уравнением
, а прямая L уравнением
|
|
|


|



|



 Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость.
Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость.
 Рис.4
Рис.4
Пусть φ- угол между Q и L, а 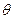 - угол между
- угол между  =(A,B,C) и
=(A,B,C) и  =(m,n,p) (Рис.4). Тогда
=(m,n,p) (Рис.4). Тогда
 ,а
,а  и так как Sinφ≥0 получим:
и так как Sinφ≥0 получим:
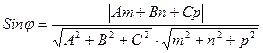 -искомый результат.
-искомый результат.
Если L || Q, то  , поэтому
, поэтому  =0, то есть
=0, то есть  является условием параллельности L и Q.
является условием параллельности L и Q.
Если L  Q, то
Q, то  и
и  ||, поэтому
||, поэтому  -условия перпендикулярности L и Q.
-условия перпендикулярности L и Q.
9. Пересечение прямой с плоскостью
Найти точку пересечения прямой  с плоскостью
с плоскостью  .
.
Для этого надо решить систему этих уравнений. Проще всего это сделать если записать уравнение прямой в параметрической форме:

Подставляя эти значения в уравнение плоскости получим 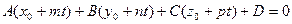 или
или  , если L не || Q, то есть если
, если L не || Q, то есть если  , то получим
, то получим  , подставляя t в записанные выше уравнение прямой в параметрической форме координат, получим их значения в точке пересечения L и Q.
, подставляя t в записанные выше уравнение прямой в параметрической форме координат, получим их значения в точке пересечения L и Q.