Независимость собственных векторов

Теорема. Собственные векторы оператора, отвечающие различным собственным значениям λ₁λ₂…..λ_n линейно независимы. Важнейшее следствие: определитель матрицы не зависит от выбора базиса.

Доказательство. Пусть - оператор в новом базисе, тогда

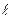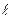т.е. при переходе к новому базису собственные числа сохраняются. Наиболее простой вид принимает матрица P линейного оператора , имеющего n линейно независимых собственных векторов с собственными значениями λ₁,λ₂…λ_n.Векторы примем за базисные. Тогда разложение векторов по базису ₁, ₂... 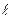_n как это следует из свойств линейных операторов, примет вид:

Отсюда следует, что если i=j и a_ij=0 если i ≠ j. Таким образом, в базисе составленном из собственных векторов, матрицы оператора будет иметь диагональный вид.

P= =

Верно и обратное если матрица P линейного оператора в некотором базисе является диагональной, то все векторы этого базиса- собственные векторы оператора .

Симметричный оператор.

Линейный оператор называется симметричным, если для любых векторов и выполняется равенство: .

Теорема. Для того, чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в ортогональном пространстве была симметрична.

Рассмотрим для простоты двухмерное пространство. Линейные операторы ₁ и ₂ определены своими матрицами

и

 

Вычислим векторы ₁() и ₂()

 

Найдем скалярные произведения :

Найдем разность скалярных произведений:

(1)

Если эта разность равна 0, то будут выполняться равенства (необходимость)

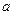₁₁= b₁₁, 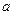₂₁ = b₁₂, , 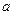₂₂=b₂₂ (2) и обратно, если только что записанные соотношения выполнены для любых и , то и равенство (1) выполнено (достаточность). Система равенств (2) означает, что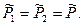

 

Ортогональность собственных векторов.

Теорема: собственные векторы симметричного линейного оператора, соответствующие различным собственным числам, взаимно ортогональны.

Пусть векторы и - собственные векторы оператора соответствующие собственным числам λ₁ и λ₂, причем λ₁≠λ₂ . По определению симметричного оператора:

. Подставляя сюда и получим . Вынесем λ₁ и λ₂ за знак скалярного произведения, перенесем все влево и разложим на множители и получим , так как λ₁≠λ₂, то =0, что означает взаимную ортогональность векторов и .

 

 

Квадратичные формы.

Пусть L=()- симметричная матрица n-го порядка, тогда выражение -называется квадратичной формой переменных x₁,x₂...x_n. Матрица L=(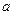 _ij) i,j=(1,2...n) -называется матрицей квадратичной формы. Пусть() –симметричная матрица, т.е. = . В матричной форме квадратичная форма имеет вид:

 

 

, где X= -матрица столбец переменных, а = - матрица строка этих же переменных. Найдем произведение этих матриц.

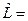
-что является по определению квадратичной формой.