Государственное образовательное учреждение
Высшего профессионального образования Тюменской области
ТЮМЕНСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ
МИРОВОЙ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА
Кафедра математики, информатики и естественных наук
Р.М. Султанаев
Высшая математика
Курс лекций
для студентов всех специальностей
очной и заочной форм обучения
(ЧАСТЬ 1)
Тюмень, 2009
ЧАСТЬ I
Введение
Математика одна из самых древних наук и появилась в связи с необходимостью количественных расчетов в окружающем человека мире. Наиболее простейший расчет – определение хотя бы числа пальцев на руке, количество добытой дичи и т.п. По мере развития общества появилась необходимость во все более сложной системе расчетов, обусловленных зарождаемым строительством, торговлей и, например, морским плаванием.
Статус самостоятельной науки математика приобрела в древней Греции и Китае еще до нашей эры. Все философские школы того времени включали математику в круг вопросов миросозерцания.
Важнейший вклад в появление математики, как самостоятельной науки, внесли работы Евклида, Архимеда и Аристотеля. Так Евклид в своих «началах» заложил основы классической геометрии, а Архимед в малоизвестных работах разрабатывал «азы» дифференциального и интегрального счисления и теории бесконечно малых величин. Последние работы были заново выполнены только в 16-18 веках н.э. Все это привело к появлению математики переменных величин. На первый план выдвигаются понятия функции, играющие в дальнейшем такую же роль основного и самостоятельного предмета изучения как ранее известные понятия числа и величины. Именно исследование функциональных зависимостей, их описание приводит к созданию математического анализа. В дальнейшем благодаря Декарту установилась связь между геометрией и алгеброй и открылась возможность геометрической интерпретации алгебраических и аналитических данных.
Математика, как система различного рода количественных расчетов и функциональных зависимостей, используется всеми без исключения современными науками. Можно сказать, что без математики невозможно существование никакой современной науки.
Надо отметить, что новые направления в математике возникают, не только в результате запросов естественных наук, но и вследствие внутренней потребности самой математики как науки. Примером тому является неэвклидова (Риманова) геометрия, разработанная в трудах Лобачевского и Римана.
Новый толчок в развитии математики появился в связи с созданием вычислительных машин. С их появлением появилась возможность приблизительного расчета, с требуемой точностью, количественных характеристик самых различных явлений в окружающем нас микро и макро мире. Особенно большое влияние появление ЭВМ оказало на исследование явлений и процессов описываемых путем математического моделирования.
Аналитическое решение применительно к сложным математическим моделям оказывалось почти всегда невозможным, а с помощью ЭВМ, возможно, получить результат с достаточной точностью.
Точно такой же подход используется экономистами для развития наших представлений об экономиках различных типов.
I. Линейная алгебра.
I. Матрицы.
Основные понятия.
Понятие матрицы и основанный на нем раздел математики – матричная алгебра имеет большое значение для экономистов. Дело в том, что большая часть математических моделей используемых при описании экономических процессов записывается в матричной форме.
Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк одинаковой длины n – столбцов. Числа, составляющие матрицу, называются элементами матрицы. Матрица записывается в виде:
 A=
A= 

Или сокращенно А =(a ij)  , где i = 1, m (т.е. i=1,2,…m) – номер строки, j =1, n (т.е. j=1,2,3,…n) – номер столбца. Матрицу А называют матрицей размера m×n и пишут A m×n. Элементы, стоящие на диагонали идущей из верхнего угла образуют главную диагональ.
, где i = 1, m (т.е. i=1,2,…m) – номер строки, j =1, n (т.е. j=1,2,3,…n) – номер столбца. Матрицу А называют матрицей размера m×n и пишут A m×n. Элементы, стоящие на диагонали идущей из верхнего угла образуют главную диагональ.
Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т.е. А = В, если a ij = b ij, где i = 1… m, j = 1… n.
Матрица, у которой число строк равно числу столбцов называется квадратной. Квадратную матрицу размера n×п называют матрицей n- порядка.
Квадратная матрица, у которой все элементы кроме элементов главной диагонали равны нулю, называется – диагональной.
Диагональная матрица, у которой каждый элемент равен единице, называется единичной. Обозначают буквой Е.
Пример: Е 3х3=  - единичная матрица 3-его порядка
- единичная матрица 3-его порядка

 Пример: Е nхn=
Пример: Е nхn=  –единичная матрица n-го порядка
–единичная матрица n-го порядка
Квадратная матрица называется треугольной если все элементы, расположенные по одну сторону от главной диагонали равны 0 (нулю).
Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О, Имеет Вид:
О = 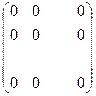
В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике. Матрицу, содержащую один столбец или одну строку, называют вектором (или вектор – столбец или вектор – строка соответственно). Их вид:

 А=
А= 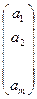 или B=
или B= 
Матрица размера 1×1, состоящая из одного числа отождествляется с этим числом т.е. (5)1×1 = 5.
Матрица, полученная из данной, заменой каждой её строки столбцом с тем же номером, называется транспонированной к данной. Обозначается АТ
Так если А= 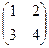 , то АТ=
, то АТ= 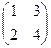 , если А=
, если А=  , то АТ=
, то АТ= 
Транспонированная матрица обладает следующим свойством: (АТ)Т = А
Действия над матрицами
а) Сложение
Операции сложения проводятся только для матриц одинаковых размеров. Суммой двух матриц Аm×n = (aij) и Bm×n = (bij) называется матрица Cm×n = (cij) такая, что cij = aij + bij (i= 1… m, j= 1… n).
Пример:
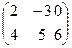 +
+  =
= 
Аналогично производится и вычитание матриц.
б) Умножение на число
Произведение матрицы Аmn=(aij) на число К называется матрица Bm×n=(bij) такая, что bij=k× aij (i= 1… m, j= 1… n).
Пример:
А=  , к=2; А·К=
, к=2; А·К= 
Матрица – А = (- 1)А называется противоположной матрице А.
Операции сложения и умножения матрицы на число обладают обычным набором арифметических свойств:
10. 
20. 
30. 
40. 
50. 
60. 
70. 
80. 
Здесь А, В, С- матрицы, а α, β –числа.
в) Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
· Перестановка двух параллельных рядов матриц
· Умножение всех элементов матрицы на число отличное от нуля
· Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда умноженных на одно и тоже число
Две матрицы называют эквивалентными если одна из них получается из другой с помощью элементарных преобразований, записывается А~В.
При помощи элементарных преобразований любую матрицу можно привести к матрице у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической. Например:

Пример: Привести к каноническому виду А= 



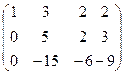









г) Произведение матриц
Умножение двух матриц А и В возможно только для случая, когда число столбцов первой матрицы равно числу строк второй (в этом случае матрица А называется согласованной с В). В этом случае произведение матрицы Аm×n=(aij) на Bn×p=(bjk) называется матрица Cm×p=(cik) такая, что cik =ai1b1k+ai2b2k+…+ainbnk, (i= 1… m, k= 1… p).
Т.е. элемент i строки и k-го столбца матрицы С, равен сумме произведений элементов i-й строки А на соответствующие элементы k-го столбца В.
Пример: 

 =
=
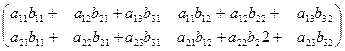

Для умножения матриц справедливы еще четыре арифметические операции:
1.)  2.)
2.) 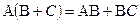

3.)  4.)
4.) 
Для операции транспортирования верны свойства:
1.) (А+В)Т = АТ + ВТ 2.) (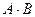 )Т =
)Т = 
Определители
Основные понятия
При решении систем уравнений, о которых мы будем говорить позже, необходимо ввести понятие определителя – числа сопоставляемого с квадратной матрицей А. Обозначается определитель так - |A|, ∆ или det A. Сопоставление должно происходить следующим образом:
а. Матрица порядка n=1, A = (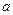 1), det A =
1), det A = 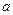 1
1
б. n=2 A=  detA=
detA=  =
= 
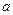 11
11 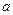 22-
22- 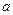 12
12 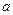 21.
21.
в.n=3 A=  ;
;
detA=  =
=  .
.
При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (Саррюса).















 =
= 

 2. Свойства определителей (необходимы для вычисления определителей):
2. Свойства определителей (необходимы для вычисления определителей):
1) Определитель не изменится, если его строки заменить столбцами и наоборот.
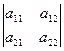 =
=  :
:
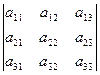 =
= 
В дальнейшем строки и столбцы будем называть просто рядами.
2) При перестановке двух параллельных рядов определитель меняет знак.
3) Определитель, имеющий два одинаковых ряда равен нулю.
4) Общий множитель элементов, какого – то ряда определителя можно вынести за знак определителя.
Из свойств 3) и 4) следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Пример:
 =
= 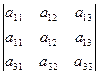
 =K·0=0
=K·0=0
5) Если элементы какого либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Пример:
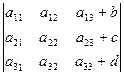 =
=  +
+ 

6) Определитель не изменится если к элементам одного ряда прибавить соответствующие элементы параллельного ряда умноженные на любое число.
Пример:
 =
=  =
=
Используя 3),4) и 5) получим ∆=

 =
=  +
+  k=∆+
k=∆+ 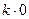 =∆
=∆
7) Теорема Лапласа: ( Разложение определителя по элементам некоторого ряда). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения. Для того чтобы понять, что такое алгебраическое дополнение необходимо ввести понятие минора. Минором некоторого элемента aij определителя n –го порядка называется определитель n- 1-го порядка полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится данный элемент, обозначается mij.
Так если: ∆= 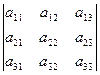 , то m11=
, то m11= 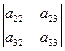 ; m32=
; m32= 
Алгебраическим дополнением элемента aij определителя называется его минор взятый со знаком «+» если сумма i+j – четное число, и со знаком «-» если сумма нечетная. Обозначается Аij
Aij =(-1)i+jmij, так A 11 =+m 11, A 32 =-m 32
Теперь вернемся к свойству 7) согласно определения для определителя∆ 3-го порядка
∆= 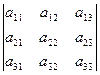 =
= 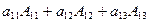
Доказательство

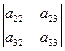 -a12
-a12  +a13
+a13  =
= 
=  ∆
∆
Последнее свойство используется для вычисления определителей высокого порядка.
8) Сумма произведений элементов, какого либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равно 0.
Пример: a 11 A 21 +a 12 A 22 +a 13 A 23 = 0.
Невырожденные матрицы
Пусть А – квадратная матрица n-го порядка.
A= 
Эта матрица называется невырожденной, если ∆≠0, в противном случае ∆=0 и матрица – вырожденная.
Обратная матрица
Матрица А-1 называется обратной матрице А, если выполняется условие  – единичная матрица того же порядка, что и матрица А. Матрица А-1 имеет те же размеры, что и матрица А.
– единичная матрица того же порядка, что и матрица А. Матрица А-1 имеет те же размеры, что и матрица А.
Теорема: Всякая невырожденная матрица имеет обратную.
Проведем доказательство для случая матрицы 3-го порядка. Пусть
A=  , причем ∆≠0
, причем ∆≠0
Рассмотрим квадратную матрицу А*,называемую союзной, элементы которой являются алгебраическими дополнениями элемента 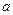 ij данной матрицы А (определяется так же, как и алгебраическое дополнение элемента определителя).
ij данной матрицы А (определяется так же, как и алгебраическое дополнение элемента определителя).
A* = 
И найдем произведение А на А*
A∙A*= 
 =
= 
 =
=
Используя свойства 6) и 7 получим)
=  =
=  =
=  (1)
(1)
Аналогично можно показать, что  (2). Равенство (1) и (2) можно записать в виде:
(2). Равенство (1) и (2) можно записать в виде:
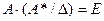 и
и 
Сравнивая эти выражения с определением обратной матрицы, получим: A-1  =
= 
Свойства обратных матриц:
1) 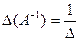
2) 
3) 
Ранг матрицы
Рассмотрим матрицу А размера m×n.
 A=
A= 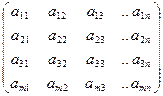
В этой матрице вычеркиванием, каких либо строк и столбцов можно вычленить квадратные подматрицы k-го порядка, где k ≤ min (m,n). Все такие определители, как мы говорили ранее, называются минорами. Наибольший порядок миноров, отличных от нуля называется рангом матрицы. Обозначается r, r (A) или rang A, очевидно, что 0 ≤ r ≤ min (m,n).
Отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным минором этой матрицы. Строки и столбцы, участвующие в образовании базисного минора, так же называются базисными. В курсе алгебры важную роль играет теорема о базисном миноре, которую мы приведем без доказательства.
Теорема: Всякая строка (столбец) матрицы является линейной комбинацией её базисных строк (столбцов).
У матрицы может быть несколько базисных миноров.
Пример: Найти ранг матрицы
A= 
Решение: Все миноры 3-го порядка равны 0. Есть минор 2=го порядка отличный от 0 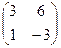 ≠-15. Значит r (A) = 2. Базисный минор стоит на пересечении 2 и 3 строки, c 1 и 3 столбцом.
≠-15. Значит r (A) = 2. Базисный минор стоит на пересечении 2 и 3 строки, c 1 и 3 столбцом.
Отметим свойства ранга матрицы:
1. При транспортировании матрицы её ранг не маняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Ранг канонической матрицы равен числу единиц на главной диагонали, что используется для вычисления ранга матрицы.
II. Система линейных уравнений.
Основные понятия
Системой m линейных алгебраических уравнений с n неизвестными называется система вида:

Здесь a ij и bj – произвольные числа (i=1,2,3…m; j=1,2,3…n) которые называются соответственно коэффициентами при неизвестных и свободными членами уравнений.
хi – неизвестные числа.
Такую систему можно записать более кратко с помощью знаков суммирования.

Или в матричной форме: А × Х = В
Здесь А – матрица коэффициентов системы называемая основной матрицей.
 n
n

 X =
X =  вектор-столбец у неизвестных xj; B =
вектор-столбец у неизвестных xj; B =  вектор-столбец из свободных членов bi.
вектор-столбец из свободных членов bi.
Х и В представляют собой векторы столбцы, однако в целях единого подхода в рамках матричной алгебры удобнее трактовать их именно как матрицы состоящие соответственно из n и m строк и одного столбца.
Произведение матрицы А×Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (п – штук).
Расширенной матрицей системы называется матрица Ā системы дополняемая столбцом свободных членов.

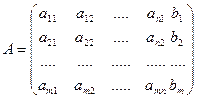
Решением системы называется п значений неизвестных xj=cj где  , при подстановке которых все уравнения системы превращаются в верное равенство (тождество). Всякое решение системы можно записать в виде матрицы-столбца.
, при подстановке которых все уравнения системы превращаются в верное равенство (тождество). Всякое решение системы можно записать в виде матрицы-столбца.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Система совместная называется определенной, если она имеет единственное решение, и неопределенной, ели она имеет более одного решения. В последнем случае каждое её решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему это, значит, выяснить, совместна она или нет. Если система совместна, то найти её общее решение.
Две системы называются эквивалентными, если они имеют одно и тоже общее решение. Другими словами системы эквивалентны, если каждое решение одной является решением другой и наоборот.
Эквивалентные системы получаются в частности при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.
Система линейных уравнений называется однородной, если все свободные члены равны 0.
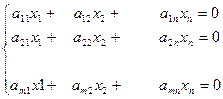
Однородная система всегда совместна так как х1=х2…=хп=0 является решением системы. Это решение называется нулевым или тривиальным.






