Пусть y= y(u), где u= u(x) – дифференцируемые функции. Тогда сложная функция y=y[u(x)] есть также дифференцируемая функция, причем
, или 
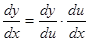
Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.
Производные сложных функций находятся при помощи таблицы:
| 
|
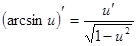
Рассмотрим примеры.
Пример 1: Найти производную функции 
Решение: 
= 
Пример 2: Найти производную функции 
Решение: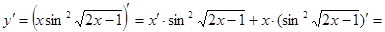 
= 
+
Производные высших порядков
Определение: Производная второго порядка (вторая производная) от функции y=f(x) есть производная от ее первой производной: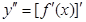 
.
Определение: Производная третьего порядка (третья производная) от функции y=f(x) есть производная от ее второй производной: 
.
Определение: Производная n-ого порядка(n -я производная) от функции y=f(x) есть производная от ее (n-1)-й производной: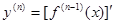 
.
Рассмотрим примеры.
Пример 1: Найти производную второго порядка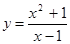 
.
Решение: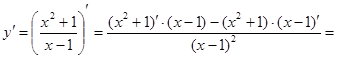 
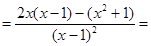
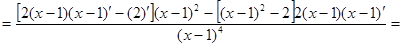
Пример2: Найти производную второго порядка функции 
.
Решение: 
Математический анализ. Интегральное исчисление
Неопределенный интеграл. Методы вычисления
Определение: Функция F(x) называется первообразнойдля функции f(x), если 
или 
.
Любая непрерывная функция f(x) имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым.
Определение: Совокупность F(x)+С всех первообразных для функции f(x) называется неопределенным интегралом от этой функции и обозначается:
.
Основные свойства неопределенного интеграла:
1. 
2. 
;
3. 
4. 
;
5. 
; 6. 
.
Непосредственное интегрирование
Непосредственное интегрирование предполагает использование при нахождении неопределенных интегралов таблицы интегралов
Таблица интегралов
 
| 
  
|
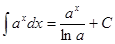
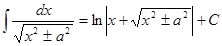
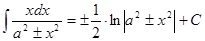
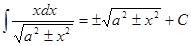
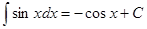
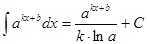
Рассмотрим нахождение интегралов непосредственным методом.
Пример 1: Найти неопределенный интеграл:
.
Решение: =
= 
.
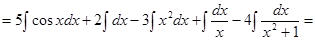
Пример 2: Найти неопределенный интеграл: 
.
Решение: = 
.
Пример 3: Найти неопределенный интеграл 
Решение: = 
Метод подстановки в неопределенном интеграле (метод замены переменной)
Этот метод заключается в том, что заменяют переменную х на 
,где -непрерывно дифференцируемая функция, полагают 
и получают 
При этом получают искомую функцию, выраженную через переменную t. Для возвращения к переменной х необходимо заменить t значением 
, которое находится из соотно-шения 
.
Рассмотрим нахождение интегралов методом подстановки.
Пример 1: Найти неопределенный интеграл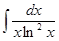 
Решение: =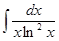 
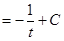
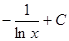
Пример 2: Найти неопределенный интеграл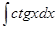 
Решение: 
= 
Пример 3: Найти неопределенный интеграл 
Решение: = 
Пример 4: Найти неопределенный интеграл 
Решение: = 
= 
= 
.
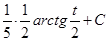