Линейная алгебра
Понятие и формы записи комплексных чисел
Комплексным числом называется выражение вида 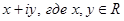 , i - символ, называемый мнимой единицей и обладающий свойством
, i - символ, называемый мнимой единицей и обладающий свойством  . Действительные числа x и y называются действительной и мнимой частями комплексного числа
. Действительные числа x и y называются действительной и мнимой частями комплексного числа  и обозначаются через Re z и Im z соответственно.
и обозначаются через Re z и Im z соответственно.
Всякое комплексное число  может быть изображено точкой M(x,y) с абсциссой x и ординатой y в координатной плоскости, называемой комплексной(см. рис. 1).
может быть изображено точкой M(x,y) с абсциссой x и ординатой y в координатной плоскости, называемой комплексной(см. рис. 1).
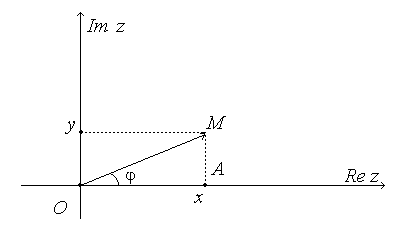
Рис. 1
Число 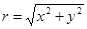 называется модулем комплексного числа
называется модулем комплексного числа  , обозначается символом |z| и равно расстоянию от начала координат О до точки M, изображающей число z.
, обозначается символом |z| и равно расстоянию от начала координат О до точки M, изображающей число z.
Угол φ между положительным направлением оси Оx и вектором 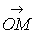 называется аргументом Arg z комплексного числа
называется аргументом Arg z комплексного числа  . При этом
. При этом  если движение от оси Ox осуществляется против часовой стрелки, и
если движение от оси Ox осуществляется против часовой стрелки, и 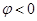 в противном случае. Значения Arg z определяется неоднозначно, с точностью до слагаемых, кратных
в противном случае. Значения Arg z определяется неоднозначно, с точностью до слагаемых, кратных 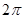 . Поэтому из всех значений Arg z выбирается главное значение, которое лежит в интервале
. Поэтому из всех значений Arg z выбирается главное значение, которое лежит в интервале 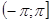 и обозначается через arg z.
и обозначается через arg z.
Главное значение arg z вычисляется по формуле
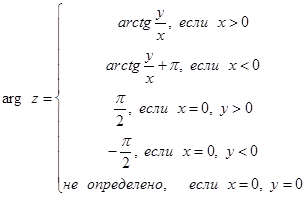
Пример 1 Для числа  имеем
имеем 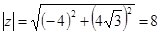
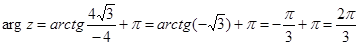
Запись 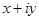 называется алгебраической формой числа z. Из прямоугольного треугольника OAM (см. рис. 1) получаем
называется алгебраической формой числа z. Из прямоугольного треугольника OAM (см. рис. 1) получаем 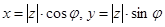 Таким образом, справедливо равенство
Таким образом, справедливо равенство
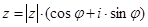
представляющее тригонометрическую форму числа z. Обозначив символом 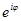 выражение
выражение  , получаем показательную форму комплексного числа z
, получаем показательную форму комплексного числа z


Например, 
Пример 2 Дано комплексное число  . Требуется записать число в алгебраической, тригонометрической и показательной формах
. Требуется записать число в алгебраической, тригонометрической и показательной формах
1. Найдем алгебраическую форму числа a:
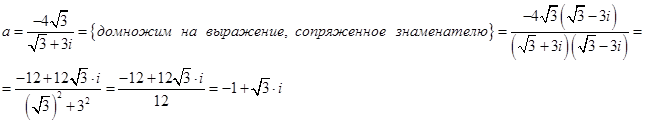 . Числу a соответствует точка М(-1;
. Числу a соответствует точка М(-1;  ), изображенная на рис. 2.
), изображенная на рис. 2.

Рис. 2
Найдем модуль и аргумент числа а
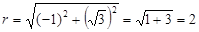 ,
, 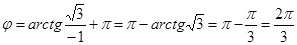
Тогда тригонометрическая и показательная формы числа а определяются равенствами

Основы дискретной математики
Теория множеств
Множество – это совокупность элементов, представляющих между собой единое целое. Имеют место различные операции над множествами. Через  обозначается отношение принадлежности, т.е. х
обозначается отношение принадлежности, т.е. х  А означает, что элемент х принадлежит множеству А. Если х не является элементом множества А, то это записывается х
А означает, что элемент х принадлежит множеству А. Если х не является элементом множества А, то это записывается х 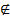 А. Два множества А и В считаются равными, если они состоят из одних и тех же элементов. Мы пишем А=В, если А и В равны, и А ≠ В в противном случае. Через
А. Два множества А и В считаются равными, если они состоят из одних и тех же элементов. Мы пишем А=В, если А и В равны, и А ≠ В в противном случае. Через 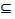 обозначается отношение включения множеств, т.е. А
обозначается отношение включения множеств, т.е. А 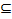 В означает, что каждый элемент множества А является элементом множества В. В этом случае А называется подмножеством В, а В — надмножеством А. Если А
В означает, что каждый элемент множества А является элементом множества В. В этом случае А называется подмножеством В, а В — надмножеством А. Если А 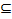 В и А≠В, то А называется собственным подмножеством В и в этом случае пишем A
В и А≠В, то А называется собственным подмножеством В и в этом случае пишем A 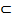 B. Множество, не содержащее элементов, называется пустым и обозначается через 0. Семейство всех подмножеств данного множества А обозначается через Р(А). Объединением множеств А и В называется множество A
B. Множество, не содержащее элементов, называется пустым и обозначается через 0. Семейство всех подмножеств данного множества А обозначается через Р(А). Объединением множеств А и В называется множество A 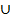 B={x │ x
B={x │ x  А или х
А или х  В}. Пересечением множеств А и В называется множество А
В}. Пересечением множеств А и В называется множество А 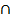 В={x │ х
В={x │ х 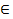 А и х
А и х 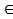 В} Разностью множеств Аи В называется множество А\В={х │ х
В} Разностью множеств Аи В называется множество А\В={х │ х 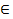 А и х
А и х 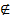 В}. Кроме того встречается обозначение «–А», которое подразумевает краткую запись U\A, где U – универсум, то есть множество, включающее в себя все другие множества. Тогда «- А» будем считать дополнением к множеству А.
В}. Кроме того встречается обозначение «–А», которое подразумевает краткую запись U\A, где U – универсум, то есть множество, включающее в себя все другие множества. Тогда «- А» будем считать дополнением к множеству А.
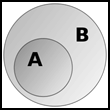
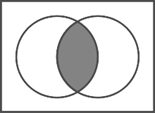
Диаграммы Венна (круги Эйлера - Венна) используются для наглядного изображения множеств. Например:
A 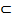 B B
| А 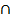 В В
| A 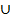 B B
| А\В |
| 
| 
| 
|
Пример 1. Используя диаграммы Эйлера – Венна докажите равенство:
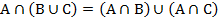
Построим диаграммы для левой и правой частей уравнения:
Выполним по порядку действий левую часть: а) 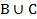 , б)
, б) 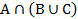
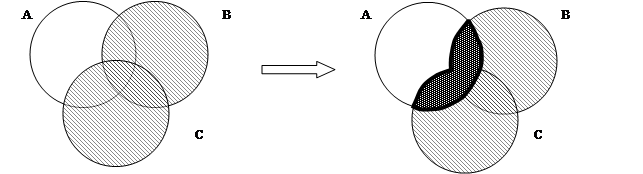
Аналогично в правой части: а)  , б)
, б) 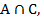 в)
в) 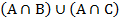
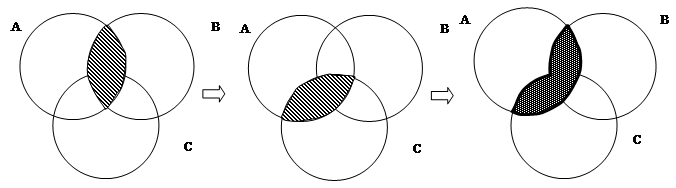 Получив две одинаковые фигуры в ответе, будем считать, что равенство доказано.
Получив две одинаковые фигуры в ответе, будем считать, что равенство доказано.
Математический анализ. Дифференциальное исчисление
Понятие производной
Определение: Производной функции 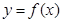 по аргументу x называется предел отношения ее приращения
по аргументу x называется предел отношения ее приращения  к приращению
к приращению 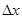 аргумента x, когда приращение аргумента стремится к нулю:
аргумента x, когда приращение аргумента стремится к нулю:
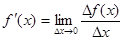 .
.
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Механический смысл производной: скорость есть первая производная пути по времени, т.е. 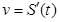 .
.
Геометрический смысл производной: тангенс угла наклона касательной к графику функции 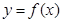 равен первой производной этой функции, вычисленной в точке касания, т.е.
равен первой производной этой функции, вычисленной в точке касания, т.е. 
Уравнение касательнойк графику функции 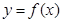 в точке
в точке  :
:

Уравнение нормали к графику функции 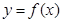 в точке
в точке  :
:
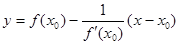
Таблица производных

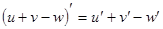
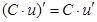
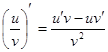
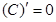
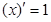

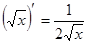
| 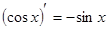




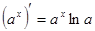 
| 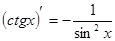
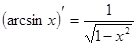
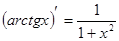
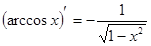
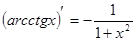
|
Процесс нахождения производных называется дифференцированием функции.
Рассмотрим примеры.
Найти производные функций:
Пример 1: 
Решение: 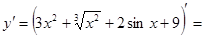


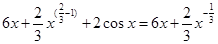 +
+

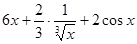
Пример2: 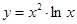
Решение: 
Пример 3: 
Решение: 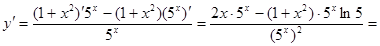
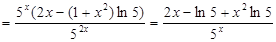
Дифференциал функции
Определение: Дифференциалом функции y=y(x) называется произведение ее производной на дифференциал независимой переменной:
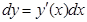 .
.
Для большей наглядности рассмотрим пример.
Пример 1: Найти дифференциал функции 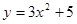
Решение: 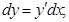
Так как 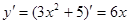 , то
, то  .
.




