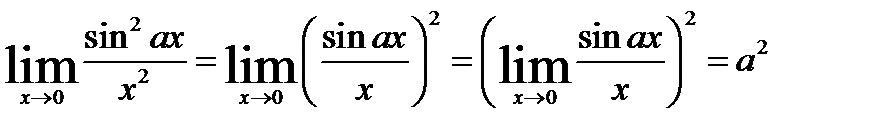При определении предела тригонометрической функции можно независимую переменную заменить ее предельным значением, если оно принадлежит области существования функции:
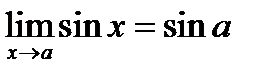
| 
| 
|
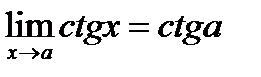
| 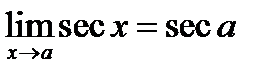
| 
|
Примеры:
1) 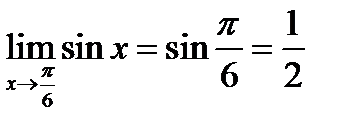
2) 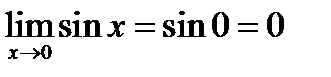
3) 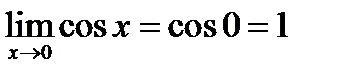
4) 
5)  - не существует, как
- не существует, как  нельзя приписать никакого числового значения.
нельзя приписать никакого числового значения.
Задача 16.1
Найти  .
.
Решение.
На основании приведенного выше правила для отыскания предела тригонометрических функций  , а потому, когда
, а потому, когда 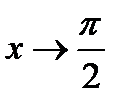 ,
, 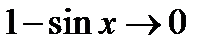 ;
;  и мы имеем дело с отношением двух бесконечно малых функций. Требуется, как уже хорошо известно читателю, специальное исследование, чтобы решить вопрос о пределе Зная. Что
и мы имеем дело с отношением двух бесконечно малых функций. Требуется, как уже хорошо известно читателю, специальное исследование, чтобы решить вопрос о пределе Зная. Что 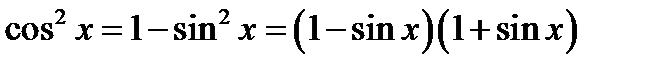 , имеем
, имеем 
 .
.
Задача 16.2
(для самостоятельного решения). Найти 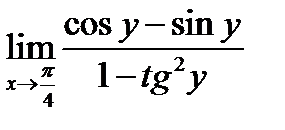 .
.
Ответ. 
Задача 16.3
(для самостоятельного решения). Найти 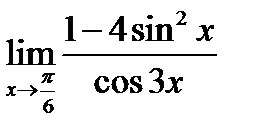 .
.
Указание. Под знаком предела находится при 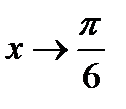 отношение двух бесконечно малых функций. Следует числитель разложить на множители:
отношение двух бесконечно малых функций. Следует числитель разложить на множители:
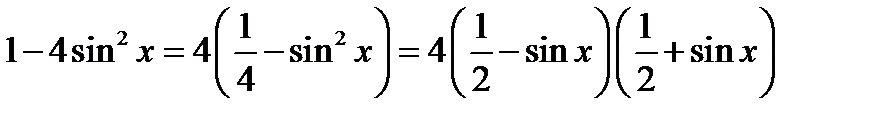 .
.
Заменить дроби
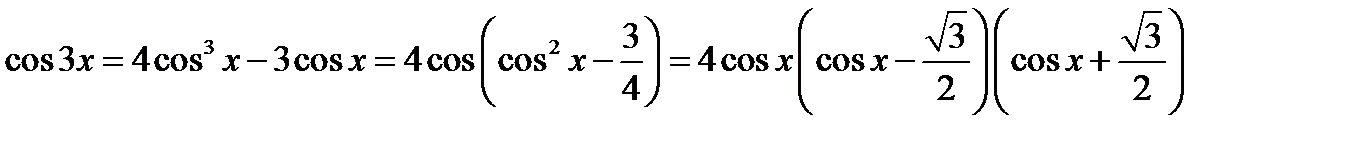
Если под знаком предела имеется сумма или разность тригонометрических функций, часто бывает полезным преобразовать их в произведение по известным формулам тригонометрии.
Учесть, что 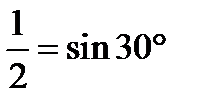 ;
; 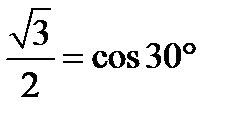
Ответ. 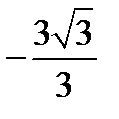 .
.
Задача 16.4
Найти 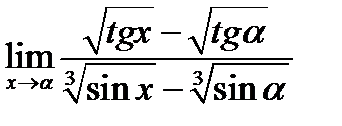 .
.
Решение.
При 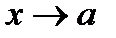 и числитель, и знаменатель дроби – функции бесконечно малые:
и числитель, и знаменатель дроби – функции бесконечно малые:
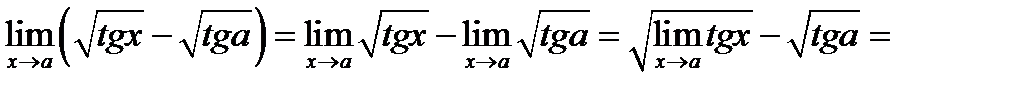
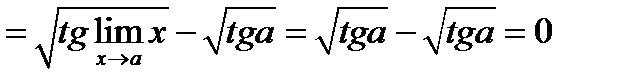 [7]
[7]
Аналогические рассуждения провести и по отношению к знаменателю. Имеем
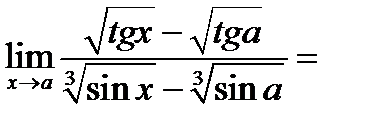
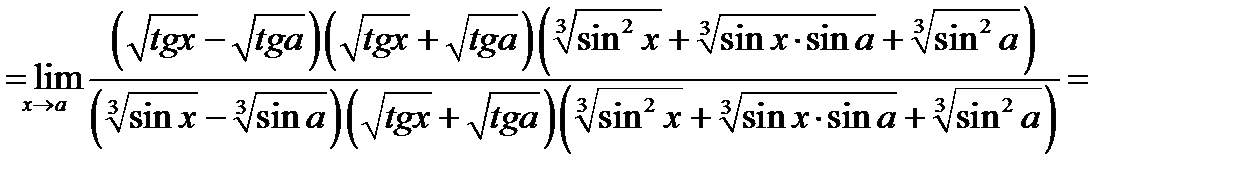
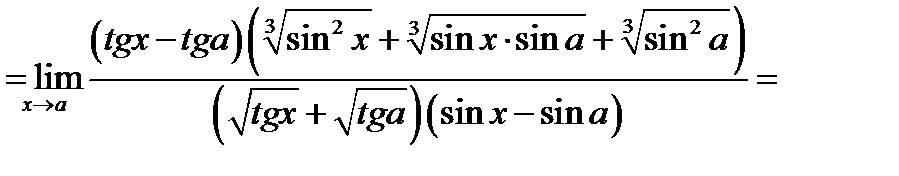
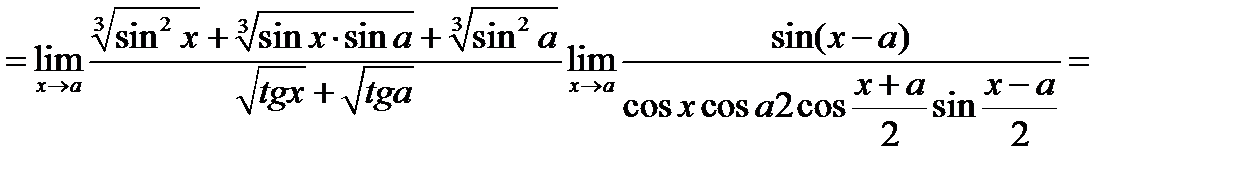
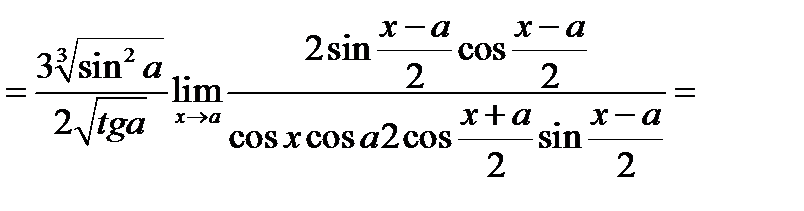

Задача 16.5
(для самостоятельного решения). Найти  .
.
Ответ.  .
.
При решении остальных задач этого практического занятия следует иметь в виду, что
(16.1) 
Задача 16.6
Найти 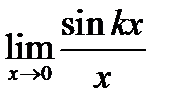 (
( - величина постоянная).
- величина постоянная).
Решение.
Иногда при отыскании предела полезно произвести замену переменной с тем, чтобы упростить отыскание предела и использовать уже известные пределы.
Если под знаком предела делается переменной, то все величины, входящие под знак предела должны быть выражены через эту новую переменную, и из равенства, выражающего зависимость между старой переменной и новой, должен быть определен предел новой переменной.
Для решения предложенной задачи сделаем такую подстановку: 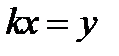 Из этого равенства следует, что
Из этого равенства следует, что  , когда
, когда 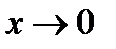 , а
, а  . Тогда
. Тогда 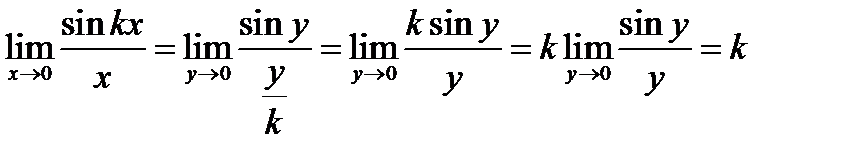 , так как
, так как 
Следует запомнить, что
(16.2) 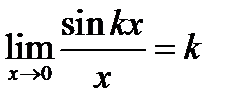
Задача 16.7
Найти  .
.
Решение.

Мы разделили числитель дроби на 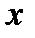 . Это можно было сделать, так как значение
. Это можно было сделать, так как значение  не должно рассматриваться. При вычислении предела числителя и знаменателя последней дроби использована формула(16.2).
не должно рассматриваться. При вычислении предела числителя и знаменателя последней дроби использована формула(16.2).
Задача 16.8
(для самостоятельного решения). Найти 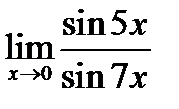 .
.
Ответ. 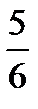
Задача 16.9
Найти 
Решение.
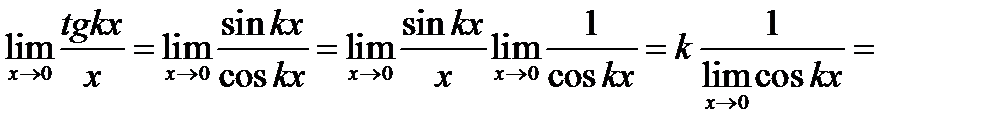
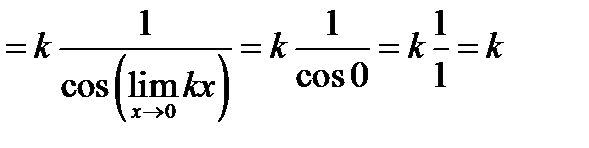
Задача 16.10
(для самостоятельного решения). Найти  .
.
Указание. Числитель и знаменатель дроби разделить на 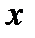 и перейти к пределу. Использовать решение предыдущей задачи.
и перейти к пределу. Использовать решение предыдущей задачи.
Ответ. 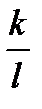
Задача 16.11
(для самостоятельного решения). Найти 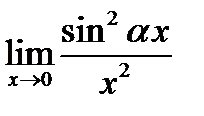 .
.
Указание. Дробь, стоящую под знаком предела, записать так:
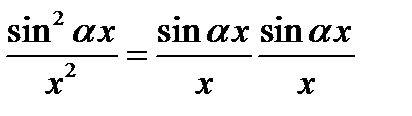
Использовать теорему о пределе произведения [8].
Ответ. 
Задача 16.12
Найти 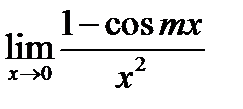 .
.
Решение.
При  числитель и знаменатель дроби – бесконечно малые функции. Воспользуемся тем, что
числитель и знаменатель дроби – бесконечно малые функции. Воспользуемся тем, что 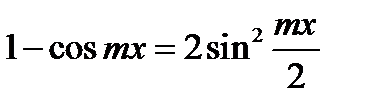 и тогда
и тогда
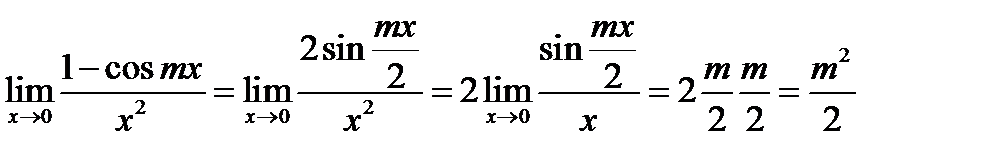
(мы использовали формулу (16.2). в нашем случае  ).
).
Задача 16.13
Найти  .
.
Решение.
При 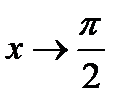 функции
функции 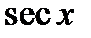 и
и 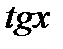 - бесконечно большие функции; таким образом, под знаком предела находится разность двух бесконечно больших функций. Теорему (14.5а о пределе разности применить нельзя, так как не существует конечных пределов каждой из функций
- бесконечно большие функции; таким образом, под знаком предела находится разность двух бесконечно больших функций. Теорему (14.5а о пределе разности применить нельзя, так как не существует конечных пределов каждой из функций  и
и  при
при  .
.
Преобразуем эту разность так:
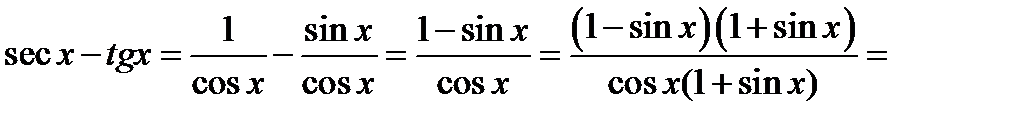

После этого получим

К последней дроби можно было применить теорему о пределе дроби, так как предел знаменателя равен2, а числитель дроби имеет конечный предел 0.
Задача 16.14
(для самостоятельного решения). Найти 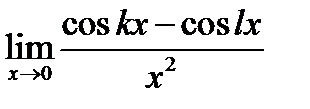 .
.
Указание. Числитель дроби равен  ; использовать так же формулу (16.2).
; использовать так же формулу (16.2).
Ответ. 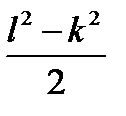
Задача 16.15
(для самостоятельного решения). Найти 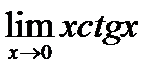 .
.
Указание. При 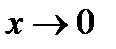 функция
функция  - бесконечно большая. а
- бесконечно большая. а  - величина бесконечно малая. Значит, мы имеем произведение функции бесконечно большой на бесконечно малую и требуется специальное исследование, чтобы определить предел этого произведения.
- величина бесконечно малая. Значит, мы имеем произведение функции бесконечно большой на бесконечно малую и требуется специальное исследование, чтобы определить предел этого произведения.
Учесть, что 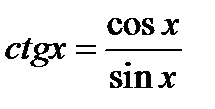 , а поэтому
, а поэтому  . На основании формулы (16.1)
. На основании формулы (16.1)  .
.
Ответ. 1.
Задача 16.16
(для самостоятельного решения). Найти 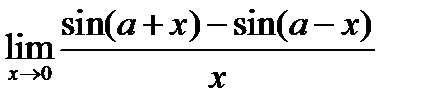
Указание.  .
.
Ответ. 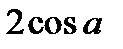
Задача 16.17
(для самостоятельного решения).Найти 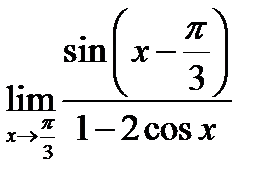 .
.
Указание. Представить числитель в виде 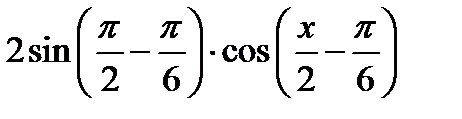 ,
,
а знаменатель 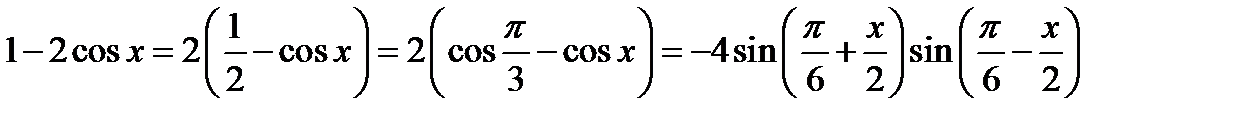 .
.
Сократить дробь и перейти к пределу.
Ответ. 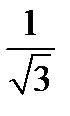
Задача 16.18
Найти 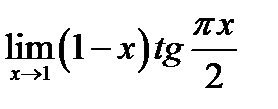 .
.
Решение.
При 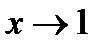 не существует предела
не существует предела  , а потому нельзя применить теорему (14.5в) о пределе произведения. Сделаем в нашем примере подстановку:
, а потому нельзя применить теорему (14.5в) о пределе произведения. Сделаем в нашем примере подстановку: 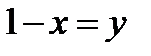 . Когда
. Когда  , то новая переменная
, то новая переменная  , так как
, так как
 Если
Если 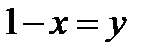 , то
, то 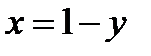 ; выражение стоящее под знаком предела, перепишется так:
; выражение стоящее под знаком предела, перепишется так:
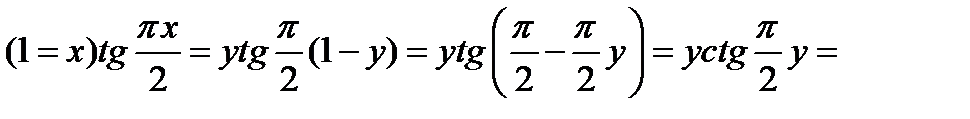
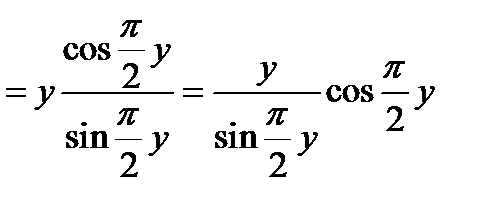 .
.
Поэтому
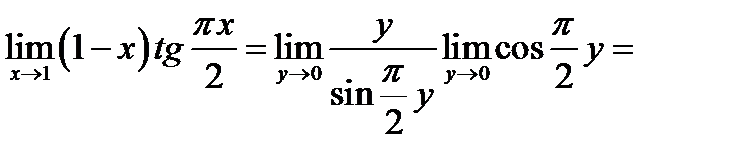
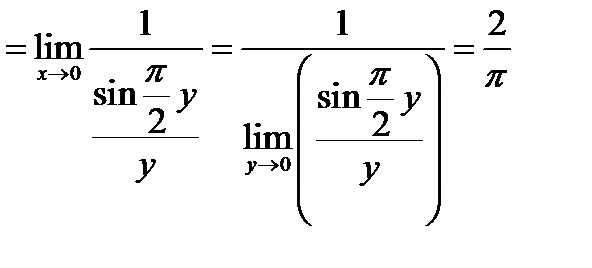 .
.
Задача 16.19
(для самостоятельного решения). Найти 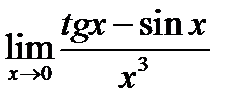 .
.
Указание. 1) 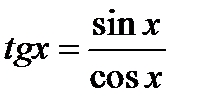 . Преобразовать дробь к виду
. Преобразовать дробь к виду 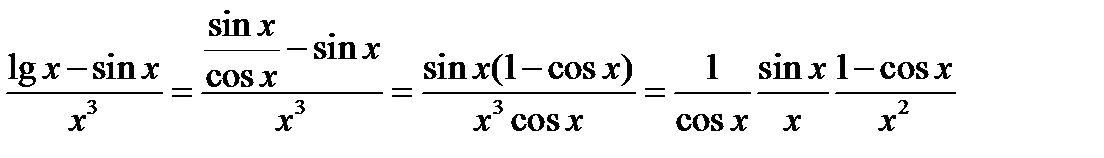 .
.
Ответ. 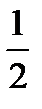
Задача 16.20
(для самостоятельного решения). Найти
1)  ;
;
2)  .
.
Указания. 1) В первом примере умножить числитель и знаменатель дроби на 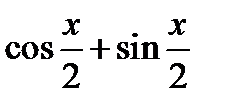 , сократить дробь и перейти к пределу. 2) во втором примере перенести иррациональность в знаменатель, сократить дробь на
, сократить дробь и перейти к пределу. 2) во втором примере перенести иррациональность в знаменатель, сократить дробь на  и перейти к пределу.
и перейти к пределу.
Ответ. 1)  ; 2)
; 2)  .
.
Задача 16.21
(для самостоятельного решения). Найти
1) 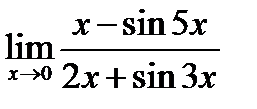 ;
;
2) 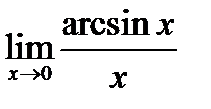 ;
;
3)  .
.
Ответ. 1) 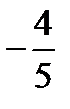 ; 2)
; 2)  ; 3)
; 3) 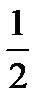 .
.
Указание. В первом приделе числитель и знаменатель дроби разделить на 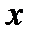 , во втором положить
, во втором положить 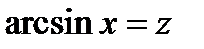 , в третьем примере
, в третьем примере 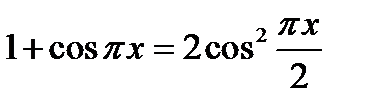 ;
; 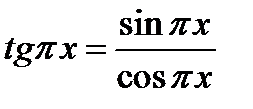 .
.
[1] *Некоторые авторы, например Г.П. Толстов в учебнике «Курс математического анализа», называют эти совокупности чисел не «полуотрезками» а «полуинтервалами».
[2] Многозначные функции нами не рассматриваются
[3] Здесь  - произвольная точка области определения функции, а
- произвольная точка области определения функции, а  - период функции.
- период функции.
[4] Натуральными числами называются все целые положительные числа.
[5] Если 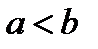 то
то 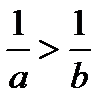 .
.
[6] Деление на 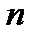 допустимо, так как предполагается, что
допустимо, так как предполагается, что 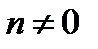 .
.
[7] 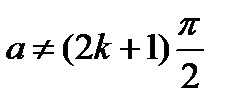 , где
, где 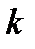 - любое целое число. Если не сделать этой оговорки, то, например, при
- любое целое число. Если не сделать этой оговорки, то, например, при  будет
будет 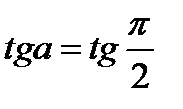 , а
, а 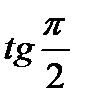 не имеет числового смысла.
не имеет числового смысла.
[8] Можно поступить и так: