Графики целых рациональных функций
Задача 4.13
Построить графики функций:
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
Решение.
1) Данную функцию нельзя отнести ни к четным ни к нечетным функциям:  .
.
Ее областью существования является бесконечный интервал  . Функция – линейная (это хорошо известно читателю из аналитической геометрии). Ее графиком является прямая линия, для построения которой достаточно знать только две ее точки. Возьмем два произвольных значения аргумента
. Функция – линейная (это хорошо известно читателю из аналитической геометрии). Ее графиком является прямая линия, для построения которой достаточно знать только две ее точки. Возьмем два произвольных значения аргумента 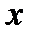 и вычислим соответствующие им значения функции
и вычислим соответствующие им значения функции  .
.
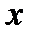
| 
|
| -2 | -14 |
Построим на плоскости точки  и
и  .
.
Прямая изображена на фиг. 4.1.

Графики остальных функций постройте самостоятельно.
Задача 4.14
Построить график функции  .
.
Решение.
Заданная функция – четная. Ее график симметричен относительно оси  . Поэтому достаточно построить часть графика для значений
. Поэтому достаточно построить часть графика для значений 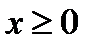 , а потом дополнить эту часть ее «зеркальным отражением» относительно оси
, а потом дополнить эту часть ее «зеркальным отражением» относительно оси  . Так будет получен полный график для этой функции. Так как функция определена при любом значении
. Так будет получен полный график для этой функции. Так как функция определена при любом значении  , составим таблицу ее значений при произвольных значениях
, составим таблицу ее значений при произвольных значениях  и построим на плоскости точки
и построим на плоскости точки 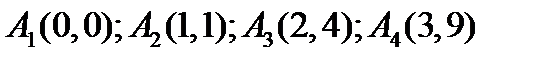 .
.
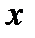
| 
|
Соединим эти точки плавной кривой (фиг.4.2).
Построим теперь «зеркальное отражение» этой кривой относительно оси  и получим полный приближенный график данной функции (фиг.4.3). Очевидно что графиком функции является парабола.
и получим полный приближенный график данной функции (фиг.4.3). Очевидно что графиком функции является парабола.
Задача 4.15
По известному графику функции  построить графики функций:
построить графики функций:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
Указание. Учесть указание 4.5 (стр.232). Пользуясь графиком функции  (фиг.4.3), сохраняя величины абсцисс, в первом случае надо увеличить все ординаты в 3 раза (фиг.4.4), во втором случае уменьшить все ординаты в 2 раза (фиг.4.5), в третьем – уменьшить их в 3 раза (фиг.4.6). В случаях четвертом и пятом использовать указание 4.2 стр.232 (фиг.4.7 и 4.8).
(фиг.4.3), сохраняя величины абсцисс, в первом случае надо увеличить все ординаты в 3 раза (фиг.4.4), во втором случае уменьшить все ординаты в 2 раза (фиг.4.5), в третьем – уменьшить их в 3 раза (фиг.4.6). В случаях четвертом и пятом использовать указание 4.2 стр.232 (фиг.4.7 и 4.8).
Задача 4.16
(для самостоятельного решения). По известному графику функции  построить графики функций:
построить графики функций: 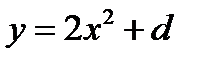 при
при  .
.
Указание. 1) Построить график функции  , использовав график функции
, использовав график функции  . Учесть указание 4.4 (стр.232). Графики этих функции показаны на фиг. 4.9 – 4.12.
. Учесть указание 4.4 (стр.232). Графики этих функции показаны на фиг. 4.9 – 4.12.
Например, график функции 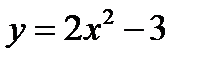 получается из графика функции
получается из графика функции 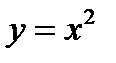 так: увеличив все ординаты этого графика в два раза при сохранении величины соответствующих абсцисс, получим график функции
так: увеличив все ординаты этого графика в два раза при сохранении величины соответствующих абсцисс, получим график функции  . Если этот график опустить на 3 ед. масштаба, то получим график функции
. Если этот график опустить на 3 ед. масштаба, то получим график функции 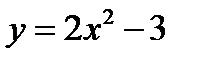 .
.
Задача 4.17
По известному графику функции  построить графики функций:
построить графики функций:
1) 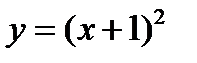 ;
;
2)  .
.
Решение.
1) График функции 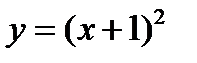 получается их графика функции
получается их графика функции  переносом его на 1 ед. масштаба вдоль оси
переносом его на 1 ед. масштаба вдоль оси 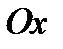 влево – фиг.4.13б (см. указание 4.3 стр. 232).
влево – фиг.4.13б (см. указание 4.3 стр. 232).
2) График функции 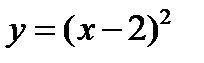 получается из графика функции
получается из графика функции  переносом его вдоль оси
переносом его вдоль оси 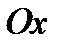 на 2 ед. масштаба вправо – фиг. 4.14а и 4.14б (использовать то же указание).
на 2 ед. масштаба вправо – фиг. 4.14а и 4.14б (использовать то же указание).
Задача 4.18
(для самостоятельного решения). По известному графику функции  построить графики функций:
построить графики функций:
1)  ;
;
2)  .
.
Задача 4.19
Пользуясь графиком функции 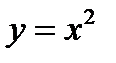 , построить график функции
, построить график функции  .
.
Решение.
Заданную функцию представим в виде 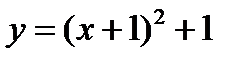 . Исходя из графика функции
. Исходя из графика функции  , построим сначала график функции
, построим сначала график функции  , а потом этот график перенесен на 1 ед. масштаба вверх (фиг.4.15) – см. указание 4.4 стр.232.
, а потом этот график перенесен на 1 ед. масштаба вверх (фиг.4.15) – см. указание 4.4 стр.232.
Задача 4.20
(для самостоятельного решения).Пользуясь графиком функции 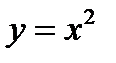 , построить график функции
, построить график функции  .
.
Указание.
Заданную функцию записать в виде  и вести построение в такой последовательности:
и вести построение в такой последовательности:
1)  ;
;
2)  ;
;
3)  ;
;
4) 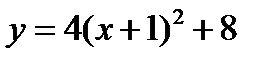 .
.
Задача 4.21
(для самостоятельного решения). Построить графики функций:
1)  ;
;
2)  ;
;
3) 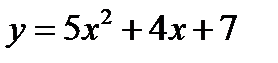 ;
;
4) 
5)  .
.
Найти также точки пересечения этих парабол с осью 
ПЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Продолжение упражнений в построении графиков функций. Графики показательной и логарифмический функции.
Задача 5.1
Построить график кубической параболы  (график этой функции, так же как и график второй степени, надо хорошо запомнить).
(график этой функции, так же как и график второй степени, надо хорошо запомнить).
Решение.
Функция 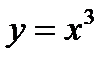 определена при всех значениях
определена при всех значениях 
 . Функция эта нечетная
. Функция эта нечетная  . Поэтому мы построим сначала ту часть ее графика которая соответствует значениям
. Поэтому мы построим сначала ту часть ее графика которая соответствует значениям  , а затем для построения полного графика воспользуемся указанием к построению графика нечетной функции (стр. 231). Так как данная функция определена при любом значении
, а затем для построения полного графика воспользуемся указанием к построению графика нечетной функции (стр. 231). Так как данная функция определена при любом значении  , то мы можем составить таблиц числовых значений аргумента.
, то мы можем составить таблиц числовых значений аргумента.
1) Построим точки  и соединяем их плавной кривой. Построим после этого кривую, симметричную этой кривой относительно начала координат.
и соединяем их плавной кривой. Построим после этого кривую, симметричную этой кривой относительно начала координат.
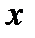
| 
|
Вся полученная кривая и будет приближенным графиком функции  (фиг. 5.1).
(фиг. 5.1).
Задача 5.2
(для самостоятельного решения). Зная график функции  , построить графики функций:
, построить графики функций:
1)  ;
;
2) 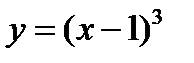 ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7)  ;
;
8) 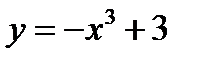 ;
;
9)  ;
;
Указание. Построение этих графиков следует выполнять на основании указаний 4.1 – 4.6 стр.232 (см. фиг. 5.2 – 5.6).
Задача 5.3
(для самостоятельного решения). Построить графики параболы четвертой степени  и, пользуясь им, построить графики функций:
и, пользуясь им, построить графики функций:
1)  ;
;
2)  ;
;
3) 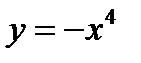 ;
;
4) 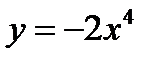 ;
;
5)  ;
;
6)  ;
;
7)  .
.
(графики удобно строить на одном чертеже, используя указания 4.3 – 4.7).
Задача 5.4
Построить график функции 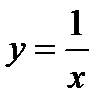 (функция
(функция 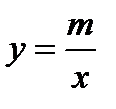 выражает закон обратной пропорциональности между переменными
выражает закон обратной пропорциональности между переменными  и
и 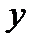 , а ее график называется графиком обратной пропорциональности).
, а ее график называется графиком обратной пропорциональности).
Решение.
Прежде всего замечаем, что заданная функция – нечетная, так как  .
.
Функция  определена при всех значениях
определена при всех значениях  , кроме
, кроме  . Ее область существования состоит из двух бесконечных интервалов
. Ее область существования состоит из двух бесконечных интервалов  и
и  .
.
Построим часть графика для значений 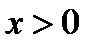 , а полный график функции получим на основании указания для построения графика нечетной функции (стр.231). Составим таблицу числовых значений функции для положительных значений аргумента.
, а полный график функции получим на основании указания для построения графика нечетной функции (стр.231). Составим таблицу числовых значений функции для положительных значений аргумента.
Построим на плоскости точки

| 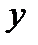
|

| |

| |

| |

| |

| |

|
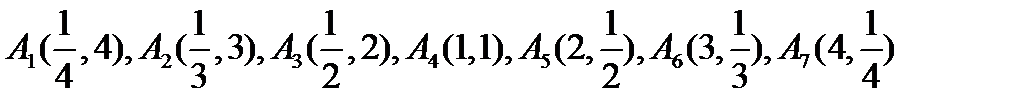 , соединим их плавной линией. Теперь построим кривую, симметричную ей относительно начала координат, и получим приближенный полный график функции (фиг.5.7)
, соединим их плавной линией. Теперь построим кривую, симметричную ей относительно начала координат, и получим приближенный полный график функции (фиг.5.7)
 .
.
Эта кривая, как известно читателю аналитической геометрии,—равнобочная гипербола (иногда говорят равноосная гипербола).
График этой функции был уже рассмотрен в первой части этого пособия. Там же был рассмотрен и график дробнолинейной функции вида 
Читателю рекомендуется повторить относящиеся сюда вопросы.
Графики показательной и логарифмической функции
Задача5.5
Построить график функции  . Считая этот график исходным, построить график функций:
. Считая этот график исходным, построить график функций:
1)  ;
;
2)  ;
;
3)  .
.
Решение.
Показательная функция  определена при всех значениях
определена при всех значениях  . Ее областью существования является бесконечный интервал
. Ее областью существования является бесконечный интервал  . Составим таблицу числовых значений функции, давая аргументу произвольные значения.
. Составим таблицу числовых значений функции, давая аргументу произвольные значения.
Построим на плоскости эти точки, соединим их плавной кривой линией и получим приближенный график данной функции (фиг.5.8а)
1) График функции 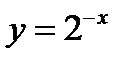 симметричен функции
симметричен функции 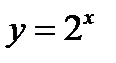 относительно оси
относительно оси  (фиг.5.8б), т.к. если
(фиг.5.8б), т.к. если  , то
, то  (см. указание 4.1 на стрю232).
(см. указание 4.1 на стрю232).

| 
|
| -5 | 
|
| -4 | 
|
| -3 | 
|
| -2 | 
|
| -1 | 
|
2) График функции  симметричен графику функции
симметричен графику функции  относительно оси
относительно оси 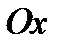 —см.указание 4.2,стр. 232(фиг5.8в).
—см.указание 4.2,стр. 232(фиг5.8в).
3) График функции  симметричен графику функции
симметричен графику функции  относительно оси
относительно оси 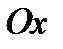 (фиг.5.8г) – см. указание 4.2 стр.232.
(фиг.5.8г) – см. указание 4.2 стр.232.
Задача 5.6
(для самостоятельного решения). Построить график функции  и, считая его исходным, построить графики функций:
и, считая его исходным, построить графики функций:
1)  ;
;
2)  ;
;
3) 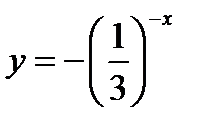 .
.
Задача 5.7
Построить график функции  , считая исходным график функции
, считая исходным график функции  .
.
Решение.
Для построения графика функции  по исходному графику
по исходному графику  следует воспользоваться указанием 4.6(стр.232).
следует воспользоваться указанием 4.6(стр.232).
Сначала построим график функции  . На этом графике выбираем только несколько точек. На том же чертеже построим точки, ординаты которых равны ординатам выбранных точек, но с абсциссами в два раза меньшими, чем у них (на фиг.5.9 на графике функции
. На этом графике выбираем только несколько точек. На том же чертеже построим точки, ординаты которых равны ординатам выбранных точек, но с абсциссами в два раза меньшими, чем у них (на фиг.5.9 на графике функции  выбраны точки
выбраны точки 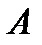 ,
,  и
и  ). Полученные точки соединим плавной кривой линией, которая и будет приближенным графиком функции
). Полученные точки соединим плавной кривой линией, которая и будет приближенным графиком функции  .
.
Задача 5.8
(для самостоятельного решения). Считая исходным график функции 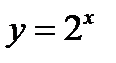 , построить график функции
, построить график функции  .
.
Задача 5.9
(для самостоятельного решения). Построить график функции 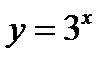 и, считая его исходным, построить графики функций:
и, считая его исходным, построить графики функций:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
Указание. При построении графиков функции 1) и 2) использовать указание 4.4 (стр 232), а при построении графика функции 4) использовать указание 4.6 стр.232.
Задача 5.10
Построить график функции 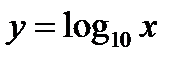 .
.
Решение.
Заданная функция определена только для значений 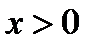 . Составим таблицу числовых значений функции при некоторых произвольно выбранных положительных значениях аргумента. Построим на плоскости точки, абсциссы которых равны значениям аргумента, а ординаты – соответствующим им значениям функции.
. Составим таблицу числовых значений функции при некоторых произвольно выбранных положительных значениях аргумента. Построим на плоскости точки, абсциссы которых равны значениям аргумента, а ординаты – соответствующим им значениям функции.

| 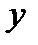
|

| -2 |

| -1 |
| 0,3010 | |
| 0,4771 | |
| 0,6021 |
Построенные точки соединим плавной кривой линией и получим приближенный график данной функции (фиг.5.10)
Задача 5.11
(для самостоятельного решения). Зная график функции  , построить графики функций
, построить графики функций
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
Указание к 4)  .
.
Использовать также указание 4.2(стр.232).
ШЕСТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Построение графиков тригонометрических и обратных тригонометрических функций






