Число  называется пределом функции
называется пределом функции  при
при  , стремящемся к
, стремящемся к  (или в точке
(или в точке  ), если для любого наперед заданного положительного числа
), если для любого наперед заданного положительного числа  (хотя бы и как угодно малого) можно найти такое положительное число
(хотя бы и как угодно малого) можно найти такое положительное число  , что для всех значений
, что для всех значений  , входящих в область определения функции, отличных от
, входящих в область определения функции, отличных от  и удовлетворяющих условию
и удовлетворяющих условию  , имеет место неравенство
, имеет место неравенство 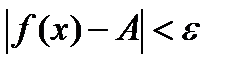 .
.
Короче: число  называется пределом функции
называется пределом функции  при
при  , стремящемся к
, стремящемся к  , если выполнение неравенства
, если выполнение неравенства  влечет за собой выполнение неравенства
влечет за собой выполнение неравенства  , где
, где  - наперед заданное число, а
- наперед заданное число, а  соответствующим образом подобрано.
соответствующим образом подобрано.
В определении предела функции следует обратить внимание на то, что вовсе не требуется, чтобы функция 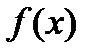 была непременно определена в точке
была непременно определена в точке  . Для того чтобы функция
. Для того чтобы функция  имела возможность стремиться к пределу при
имела возможность стремиться к пределу при  , необходимо лишь чтобы в области ее существования были точки, как угодно близкие к
, необходимо лишь чтобы в области ее существования были точки, как угодно близкие к  и отличные от
и отличные от 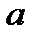 .
.
14.1. Бесконечно малые и бесконечно большие функции.
а) Функция  называется бесконечно малой при
называется бесконечно малой при  , если
, если
(14.1) 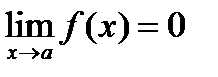 .
.
б) Функция  называется бесконечно большой при
называется бесконечно большой при  если имеет место одно из равенств
если имеет место одно из равенств
 .
.
с) Функция  называется ограниченной при
называется ограниченной при  , если существует такое положительное число
, если существует такое положительное число  , что для всех значений
, что для всех значений  из окрестности числа
из окрестности числа  выполняется неравенство
выполняется неравенство  .
.
14.2. Свойства бесконечно малых функций.
а) Если функция 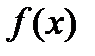 бесконечно мала при
бесконечно мала при  , то и
, то и  также мала при
также мала при  .
.
б) Если функции  и
и  бесконечно малы при
бесконечно малы при  , то сумма их, а также и разность их:
, то сумма их, а также и разность их:  и
и  бесконечно малы при
бесконечно малы при  (это утверждение распространяется на любое фиксированное число функций).
(это утверждение распространяется на любое фиксированное число функций).
с) Если при 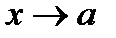 функция
функция  бесконечно мала, а функция
бесконечно мала, а функция  - ограничена, то их произведение
- ограничена, то их произведение  есть функция бесконечно малая.
есть функция бесконечно малая.
14.3. Свойства бесконечно малых функций.
Если при  функция
функция  имеет конечный предел
имеет конечный предел  , а функция
, а функция  - бесконечно велика
- бесконечно велика  , то
, то
а) сумма их – бесконечно велика, т.е.  . Предел отношения
. Предел отношения  к
к  равен нулю:
равен нулю:  .
.
б) если  , а
, а  , причем
, причем 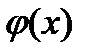 положительна в окрестности точки
положительна в окрестности точки  , то
, то 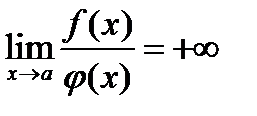 .
.
с) при положительном  , если
, если  , то
, то  .
.
д) произведение двух бесконечно больших функций бесконечно большая, т.е если  и
и  , то и
, то и  .
.
14.4. Связь между бесконечно большими и бесконечно малыми функциями:
а) Если при  - бесконечно большая функция, то функция
- бесконечно большая функция, то функция  бесконечно малая.
бесконечно малая.
б) Если при  функция
функция  бесконечно мала, то функция
бесконечно мала, то функция  - бесконечно большая, причем предполагается, что в окрестности точки
- бесконечно большая, причем предполагается, что в окрестности точки  функция
функция  в нуль на обращается.
в нуль на обращается.
14.5. Правила предельного перехода.
а) Если при  функция
функция  и
и  имеют конечные пределы, то и алгебраическая сумма их
имеют конечные пределы, то и алгебраическая сумма их  имеет предел, который равен сумме их пределов, т.е. если
имеет предел, который равен сумме их пределов, т.е. если  , а
, а  , то
, то  .
.
Короче (но не совсем точно): предел алгебраической суммы нескольких функций равен алгебраической сумме пределов этих функций.
б) Если при  функции
функции  и
и  имеют пределы, то их произведение
имеют пределы, то их произведение  также имеет предел, который равен произведению их пределов, т.е. если
также имеет предел, который равен произведению их пределов, т.е. если  , а
, а  , то
, то  .
.
Короче (но не совсем точно): предел произведения двух функций равен произведению пределов этих функций. Свойства а) и б) распространяются на любое фиксированное число функций.
с) Если при  функции
функции  и
и  имеют пределы и предел функции
имеют пределы и предел функции  равен нулю, то предел их частного существует и равен частному от деления их пределов, т.е. если
равен нулю, то предел их частного существует и равен частному от деления их пределов, т.е. если  , а
, а 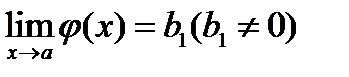 , то
, то 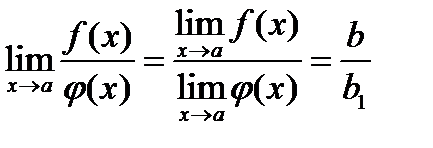
Короче (но не совсем точно): предел частного равен частному пределов если предел знаменателя не равен нулю.
14.6. Предел целой рациональной функции.
Если

То
(14.2) 
т.е. при отыскании предела целой рациональной функции можно в аналитическом выражении функции заменить аргумент его предельным значением.
14.7. Предел дробно-рациональной функции.
Если
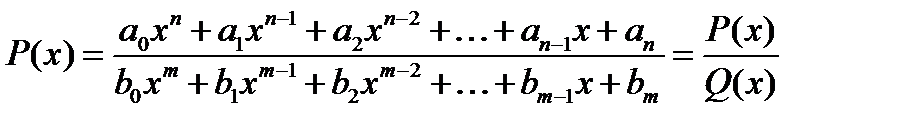 ,
,
То
(14.3)  , если
, если 
т.е. при отыскании предела дробно-рациональной функции можно в аналитическом выражении функции заменить аргумент его предельным значением, если при этом предельном значении знаменатель не обращается в нуль.
Задача 14.1
Найти  .
.
Решение.
Функция  - целая рациональная. Для отыскания ее предела применима формула (14.2). Заменим в аналитическом выражении функции
- целая рациональная. Для отыскания ее предела применима формула (14.2). Заменим в аналитическом выражении функции  его предельным значением и получим
его предельным значением и получим
 .
.
Задача 14.2
(для самостоятельного решения). Найти
1)  ;
;
2) 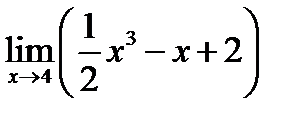 .
.
Ответ.
1)  ;
;
2)  .
.
Указание. Воспользоваться формулой (14.2).
Задача 14.3
Найти  .
.
Решение.
Здесь отыскивается предел дробно-рациональной функции. Прежде чем применять (14.3), надо проверить, не обращается ли в нуль знаменатель дроби при  . Проверяем:
. Проверяем: 

Задача 14.4
(для самостоятельного решения). Найти переделы:
1)  ;
;
2)  .
.
Указания. 1) Проверить, что знаменатель дроби в первом примере при  , а во втором при
, а во втором при  не обращается в ноль; 2) воспользоваться формулой (14.3).
не обращается в ноль; 2) воспользоваться формулой (14.3).
Ответ.
1) 0;
2)  .
.
Задача 14.5
Найти  .
.
Решение.
Знаменатель дроби  обращается в нуль при
обращается в нуль при 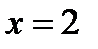 , а поэтому функция
, а поэтому функция  при
при 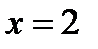 не существует.
не существует.
Теорему о пределе дроби (14.5п. с) применить нельзя, так как предел знаменателя равен нулю. По той же причине нельзя применит и формулу (14.3). Но определение предела функции содержит существующую оговорку: при отыскании предела функции  при
при  значение функции
значение функции  при
при  может не рассматриваться. От функции
может не рассматриваться. От функции  это определение не требует, чтобы точка
это определение не требует, чтобы точка  входила в область существования функции. Поэтому значение
входила в область существования функции. Поэтому значение  может нами не приниматься во внимание. Именно эти соображения и дадут возможность решить задачу. В нашем случае мы должны считать, что
может нами не приниматься во внимание. Именно эти соображения и дадут возможность решить задачу. В нашем случае мы должны считать, что  , стремясь к 2,никогда не становиться равным 2, а потому значение функции
, стремясь к 2,никогда не становиться равным 2, а потому значение функции 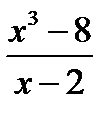 при
при  нас не интересует.
нас не интересует.
При  и числитель и знаменатель, и знаменатель дроби обращается в нуль. Мы имеем в данном случае отношение двух бесконечно малых функций, о котором без специального исследования ничего определенного сказать нельзя. Для решения задачи разделим числитель и знаменатель дроби
и числитель и знаменатель, и знаменатель дроби обращается в нуль. Мы имеем в данном случае отношение двух бесконечно малых функций, о котором без специального исследования ничего определенного сказать нельзя. Для решения задачи разделим числитель и знаменатель дроби 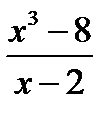 на
на  . Мы имеем право это сделать потому, что значение
. Мы имеем право это сделать потому, что значение  не рассматривается и, значит,
не рассматривается и, значит, 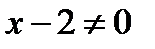
Если бы указанной оговорки а определении предела функции не было и мы должны были бы рассматривать и значение  , то разделить числитель и знаменатель дроби на
, то разделить числитель и знаменатель дроби на  мы не смогли бы, так как такое деление означало бы деление числителя и знаменателя дроби на нуль, что, конечно, недопустимо. После сокращения дроби на
мы не смогли бы, так как такое деление означало бы деление числителя и знаменателя дроби на нуль, что, конечно, недопустимо. После сокращения дроби на  получим
получим
 ,
,
И нам придется отыскать предел на данной функции, а функции 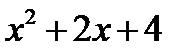 . Тогда перед учащимся должен возникнуть такой вопрос: тождественны ли функции
. Тогда перед учащимся должен возникнуть такой вопрос: тождественны ли функции 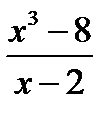 и
и 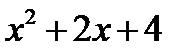 . Этот вопрос имеет положительный ответ: функции тождественны, если не рассматривать значения
. Этот вопрос имеет положительный ответ: функции тождественны, если не рассматривать значения  . Следует иметь ввиду, что две функции тождественны, если они удовлетворяют таким двум требованиям:
. Следует иметь ввиду, что две функции тождественны, если они удовлетворяют таким двум требованиям:
1) Их области существования совпадают и
2) При одном и том же значении аргумента, взятом из области существования функции, численные значения функции равны.
В нашем случае эти два требования будут выполнены, если не рассматривать значения  , но ведь оно и не рассматривается. Таким образом,
, но ведь оно и не рассматривается. Таким образом,

Так как функция 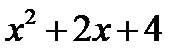 -целая рациональная функция и для определения ее предела на основании формулы (14.2) следует в аналитическом выражении функции заменить аргумент его предельным значением.
-целая рациональная функция и для определения ее предела на основании формулы (14.2) следует в аналитическом выражении функции заменить аргумент его предельным значением.
Можно указать такое
Правило. Для того чтобы определить предел дробно-рациональной функции в случае, когда при  числитель и знаменатель дроби имеют пределы, равные нулю, надо числитель и знаменатель дроби разделить на
числитель и знаменатель дроби имеют пределы, равные нулю, надо числитель и знаменатель дроби разделить на 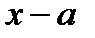 и перейти к пределу.
и перейти к пределу.
Если и после этого числитель и знаменатель новой дроби имеют пределы, равные нулю при  , то надо произвести повторное деление на
, то надо произвести повторное деление на  (это правило основывается на известном из элементарной алгебры следствии из теоремы Безу, согласно которому, если многочлен обращается в нуль при
(это правило основывается на известном из элементарной алгебры следствии из теоремы Безу, согласно которому, если многочлен обращается в нуль при  , то он делится без остатка на
, то он делится без остатка на  ).
).
Теперь для самостоятельного решения будет предложен ряд задач на определение предела дробно-рациональной функции.
Задача 14.6
(для самостоятельного решения). Найти  .
.
Указание. При  числитель и знаменатель дроби – функции бесконечно малые, пределы их равны нулю. Об их отношении без специального исследовании ничего определенного сказать нельзя. Теорему 14.5п.
числитель и знаменатель дроби – функции бесконечно малые, пределы их равны нулю. Об их отношении без специального исследовании ничего определенного сказать нельзя. Теорему 14.5п.  о пределе дроби применить нельзя, так как предел знаменателя равен нулю. Следует применить указанное правило; разделить числитель и знаменатель дроби на
о пределе дроби применить нельзя, так как предел знаменателя равен нулю. Следует применить указанное правило; разделить числитель и знаменатель дроби на  . Повторить рассуждения предыдущей задачи о допустимости такого решения.
. Повторить рассуждения предыдущей задачи о допустимости такого решения.
Ответ. 
Следует не только запомнить тот или иной прием, но главное - понять, на чем основано его применение, и каждое действие проводить совершенно сознательно, а не автоматически, «по правилам». Применяя правило, надо понимать те положения, из которых оно выведено.
Задача 14.7
(для самостоятельного решения). Найти  .
.
Указание. Здесь опять-таки функции, состоящие в числителе и знаменателе дроби, бесконечно малы при  . Для решения вопроса о предел их отношения следует разделить числитель и знаменатель дроби на
. Для решения вопроса о предел их отношения следует разделить числитель и знаменатель дроби на  . Этим указанием воспользуйтесь и при решении двух следующих задач.
. Этим указанием воспользуйтесь и при решении двух следующих задач.
Ответ. 
Задача 14.8
(для самостоятельного решения). Найти  .
.
Ответ. 
Задача 14.9
(для самостоятельного решения). Найти  .
.
Ответ.  .
.
Задача 14.10
Найти  (
( и
и  - целые положительные числа).
- целые положительные числа).
Решение.
При  числитель и знаменатель дроби имеют предел, равный нулю, а поэтому это функции бесконечно малы. Для решения вопроса о пределе их отношения следует числитель и знаменатель разделить на
числитель и знаменатель дроби имеют предел, равный нулю, а поэтому это функции бесконечно малы. Для решения вопроса о пределе их отношения следует числитель и знаменатель разделить на  . Допустимость такого деления подробно была объяснена в задаче (14.5). Повторяем, что
. Допустимость такого деления подробно была объяснена в задаче (14.5). Повторяем, что  , стремясь к 1, не становится равным 1, а потому
, стремясь к 1, не становится равным 1, а потому  , и деление на
, и деление на 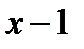 имеет смысл.
имеет смысл.
Функция  при
при  не существует, но значение
не существует, но значение 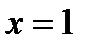 нашему рассмотрению не должно подлежать. Воспользуемся известной формулой алгебры
нашему рассмотрению не должно подлежать. Воспользуемся известной формулой алгебры
(14.4) 
Полагая здесь  , а
, а  , в нашем случае получим
, в нашем случае получим

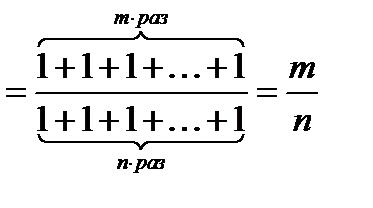
Задача 14.11
Найти 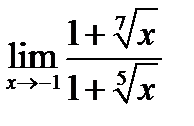 .
.
Решение.
При 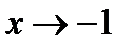 числитель и знаменатель дроби имеют пределы, равные нулю, а потом это функции – бесконечно малые. Чтобы можно было применить формулу (14.4), с помощью которой была решена предыдущая задача, следует сделать подстановку
числитель и знаменатель дроби имеют пределы, равные нулю, а потом это функции – бесконечно малые. Чтобы можно было применить формулу (14.4), с помощью которой была решена предыдущая задача, следует сделать подстановку 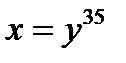 , где показатель степени 35 – наименьшее кратное показателей корней.
, где показатель степени 35 – наименьшее кратное показателей корней.
Если  , то
, то  , а
, а  , и тогда
, и тогда 
Причем  , когда
, когда  , и задача перепишется так:
, и задача перепишется так:

Теперь следует разделить числитель и знаменатель дроби на  применить формулу (14.3).
применить формулу (14.3).
Ответ.  .
.
Задача 14.12
(для самостоятельного решения). Найти:
1) 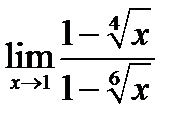 ;
;
2)  .
.
Ответ.
1)  ;
;
2)  .
.
Задача 14.13
Найти  .
.
Решение.
При  имеем
имеем
Придел числителя:
 .
.
Предел знаменателя:
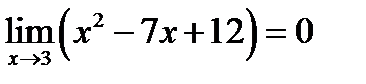 .
.
Теорема (14.5 п.с) о пределе дроби неприменима. Рассмотрим обратную дробь  , и не предел при
, и не предел при 

(здесь теорема о пределе дроби применима, так как предел знаменателя 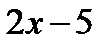 не равен нулю). Так как предел функции
не равен нулю). Так как предел функции  равен нулю, то эта функция при
равен нулю, то эта функция при  бесконечно малая, а потом функция
бесконечно малая, а потом функция  при
при  - бесконечно большая, и тогда ее предел
- бесконечно большая, и тогда ее предел 
(мы воспользовались теоремой 14.4 пункт (б).
Задача 14.14
(для самостоятельного решения). Найти  .
.
Ответ. 
Задача 14.15
(для самостоятельного решения). Найти 
Ответ.  .
.
Задача 14.22
(для самостоятельного решения). Найти  .
.
Указание. Произвести вычитание дробей.
Ответ. 
Задача 14.16
(для самостоятельного решения). Найти 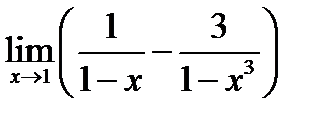 .
.
Ответ.  .
.
Указание. После приведения к общему знаменателю окажется, что при 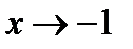 числитель и знаменатель - функции бесконечно малые. Воспользоваться указанным на стр. 304 правилом.
числитель и знаменатель - функции бесконечно малые. Воспользоваться указанным на стр. 304 правилом.
ПЯТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Продолжение упражнений на нахождение предела функции.
Решим несколько задач на нахождение предела дробно-рациональной функции при  .
.
Задача 15.1
Найти 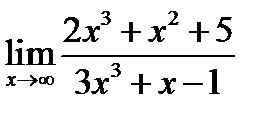 .
.
Решение.
Для того чтобы можно было применить теорему о пределе дроби, надо, чтобы числитель и знаменатель дроби имели приделы и чтобы придел знаменателя не был равен нулю. В данном случае это теорема неприменима, так как пределы числителя и знаменателя дроби не существуют При  и числитель и знаменатель дроби функции бесконечно большие (см. теоремы 14.4 о свойствах бесконечно больших функций. Рекомендуется еще раз повторить эти теоремы). Значит мы имеем дело с отношением бесконечно больших функций. Об этом отношении, так же как и об отношении двух бесконечно малых функций, ничего определенного без специального исследования сказать нельзя. Для решения задачи следует применить прием, знакомый из решения задачи 12.1 (полезно также возвратиться к задаче 12.8): дроби разделить на высшую степень
и числитель и знаменатель дроби функции бесконечно большие (см. теоремы 14.4 о свойствах бесконечно больших функций. Рекомендуется еще раз повторить эти теоремы). Значит мы имеем дело с отношением бесконечно больших функций. Об этом отношении, так же как и об отношении двух бесконечно малых функций, ничего определенного без специального исследования сказать нельзя. Для решения задачи следует применить прием, знакомый из решения задачи 12.1 (полезно также возвратиться к задаче 12.8): дроби разделить на высшую степень  , встречающуюся в членах дроби, а после этого перейти к пределу
, встречающуюся в членах дроби, а после этого перейти к пределу
Итак.


Так как при 
 - величина бесконечно малая, а поэтому и
- величина бесконечно малая, а поэтому и 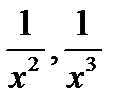
 - величины бесконечно малые (см. теоремы 14.4);
- величины бесконечно малые (см. теоремы 14.4);  ;
;  , а
, а  и пределы этих величин равны нулю, когда
и пределы этих величин равны нулю, когда  .
.
После деления числителя и знаменателя на  оказалось возможным применить теорему о пределе дроби, так как теперь и числитель, и знаменатель дроби имеют пределы, равные соответственно 2 и 3, и предел знаменателя не равен нулю.
оказалось возможным применить теорему о пределе дроби, так как теперь и числитель, и знаменатель дроби имеют пределы, равные соответственно 2 и 3, и предел знаменателя не равен нулю.
Для самостоятельного решения предлагается несколько логических задач.
Задача 15.2
(для самостоятельного решения). Найти:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
Ответ. 1) 5; 2)0; 3) 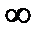 ; 4)
; 4)  ; 5)
; 5)  .
.
Задача 15.3
(для самостоятельного решения). Найти  .
.
Указание. Произвести вычитание дробей.
Ответ. 
Задача 15.4
(для самостоятельного решения). Найти  .
.
Ответ. 
Задача 15.5
(для самостоятельного решения). Найти  .
.
Ответ. 16.
Решение остальных задач этого практического занятия основано на применении теоремы:
При постоянном показателе степени можно переходить по пределу в основании степени при условии, что предел основания ступени существует, т.е.
(15.1) 
Где  - постоянная величина (для случая, когда
- постоянная величина (для случая, когда 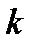 - целое число, мы этой теоремой пользовались неоднократно, так как она прямо следует из теоремы о пределе произведения).
- целое число, мы этой теоремой пользовались неоднократно, так как она прямо следует из теоремы о пределе произведения).
Из формулы (15.1) следует, что при любом нечетном  всегда
всегда
(15.2) 
Если же  - четное число, то эта формула верна только тогда, когда функция
- четное число, то эта формула верна только тогда, когда функция  - неотрицательна, т.е. когда
- неотрицательна, т.е. когда  .
.
Выполним сначала ряд простых упражнений на применение этой теоремы.
Задача 15.6
Найти:
1)  ;
;
2)  .
.
Решение.
На основании формулы (15.2) имеем:
1) 
2) 
Задача 15.7
Найти  .
.
Решение.

Задача 15.8
Найти при нечетном 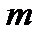
1)  ;
;
2)  ;
;
3)  .
.
Решение.
1) 
2) 
Т.е. при  функция
функция 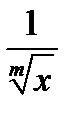 бесконечно мала;
бесконечно мала;
3) 
Так как по результатам второго примера этой задачи при  функция
функция  бесконечно мала, полому функция
бесконечно мала, полому функция  - бесконечно велика.
- бесконечно велика.
Задача 15.9
Найти  .
.
Решение.
Когда  , числитель и знаменатель имеют своим пределом нуль, а почему они бесконечно малы:
, числитель и знаменатель имеют своим пределом нуль, а почему они бесконечно малы:

Для того, чтобы решить вопрос о пределе их отношения, перенесем иррациональность а знаменатель, умножив для этого числитель и знаменатель дроби на  . Будем иметь
. Будем иметь

 .
.
Так как  , не становясь равным нулю, то деление на
, не становясь равным нулю, то деление на  числителя и знаменателя дроби возможно.
числителя и знаменателя дроби возможно.
При решении задачи мы вместо предела функции  отыскали предел функции
отыскали предел функции  ; здесь должен быть затронут вопрос о тождественности этих функций (подобно тому как этот вопрос возник при решении задачи 14.5). О функциях
; здесь должен быть затронут вопрос о тождественности этих функций (подобно тому как этот вопрос возник при решении задачи 14.5). О функциях  и
и  мы можем сказать, что они тождественны
мы можем сказать, что они тождественны  .
.
Таким образом, замена функции  при отыскании предела функцией
при отыскании предела функцией  является законной.
является законной.
При отыскании предела дроби, содержащей иррациональные выражения, в большом числе случаев приходиться с помощью преобразований переходить от заданной функции к другой заданной функции, и у учащегося должен возникать вопрос о тождественности заданной функции и той, которая получается в результате преобразований. Во всех дальнейших примерах исследованием этого вопроса мы заниматься не будем, предоставляя это читателю.
Теперь, после решения этой задачи, укажем правило для решения задач, в которых требуется определить предел дроби, содержащей иррациональные выражения в случае, когда ее числитель и знаменатель – бесконечно малые функции, т.е. когда из пределы равны нулю.
Правило. Чтобы найти предел дроби, содержащей иррациональные выражения в случае, когда предел и числителя, и знаменателя дроби равен нулю, надо перенести иррациональность из числителя в знаменатель или из знаменателя в числитель и после этого сделать необходимые упрощения, (приведение подобных членов, сокращение и т.д.) и перейти к пределу.
Задача 15.10
Найти  .
.
Решение.
При  числитель и знаменатель дроби имеют предел, равный нулю. Перенесем иррациональность в знаменатель, для чего умножим числитель и знаменатель на
числитель и знаменатель дроби имеют предел, равный нулю. Перенесем иррациональность в знаменатель, для чего умножим числитель и знаменатель на  .
.
Получим



Задача 15.11
(для самостоятельного решения). Найти пределы:
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
Ответ.
1)  ;
;
2) 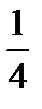 ;
;
3)  ;
;
4)  .
.
Задача 15.12
Найти 
Решение.
При  числитель и знаменатель дроби имеет предел, равный нулю. В этой задаче придется сначала числитель и знаменатель дроби умножить на
числитель и знаменатель дроби имеет предел, равный нулю. В этой задаче придется сначала числитель и знаменатель дроби умножить на  , а потом на
, а потом на  или сразу умножить числитель и знаменатель дроби на
или сразу умножить числитель и знаменатель дроби на  . Используя это указание, получаем:
. Используя это указание, получаем:





Задача 15.13
(для самостоятельного решения). Найти пределы:
1)  ;
;
2) 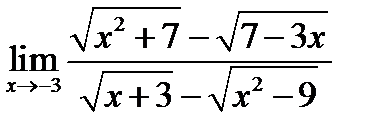 ;
;
3)  ;
;
4)  .
.
Ответ.
1)  ;
;
2) 0;
3)  ;
;
4) 
Указание. В третьем примере одним из множителей числителя будет  . Корни этого квадратного трехчлена
. Корни этого квадратного трехчлена  ;
;  , вследствие чего
, вследствие чего  .
.
Задача 15.14
Найти 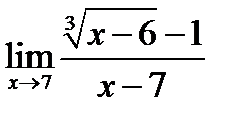 .
.
Решение.
Здесь и предел числителя, и предел знаменателя равен нулю. Перенесем иррациональность из числителя в знаменатель. Воспользуемся известной формулой алгебры  . Положим
. Положим  ,
,  . Значит, для того, чтобы получить в числителе разность кубов, надо его умножить на
. Значит, для того, чтобы получить в числителе разность кубов, надо его умножить на  . Умножая и знаменатель на эту величину получаем
. Умножая и знаменатель на эту величину получаем



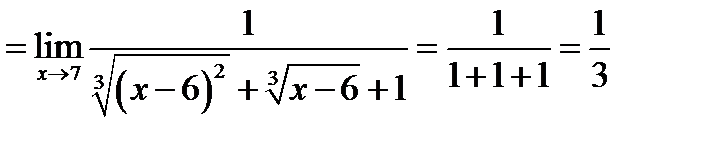 .
.
Задача 15.15
(для самостоятельного решения). Найти  .
.
Ответ. 
Задача 15.16
(для самостоятельного решения). Найти  .
.
Ответ. 
Задача 15.17
(для самостоятельного решения). Найти  .
.
Ответ. 
Задача 15.18
Найти  .
.
Решение.
Здесь непосредственно теорема 4.5 не может быть применена, так как при  пределы слагаемых не существуют: мы имеем дело с разностью двух бесконечно больших величин, о которой ничего определенного без специального исследования сказать нельзя.
пределы слагаемых не существуют: мы имеем дело с разностью двух бесконечно больших величин, о которой ничего определенного без специального исследования сказать нельзя.
Умножим и разделим данное выражение на сопряженное с ним и получим


Так как при  знаменатель дроби, стоящий под знаком предела, есть функция бесконечно большая (см. задачу 15.8(3)), а потому дробь
знаменатель дроби, стоящий под знаком предела, есть функция бесконечно большая (см. задачу 15.8(3)), а потому дробь  есть величина бесконечно малая, а ее произведение на -2 есть также бесконечно малая величина.
есть величина бесконечно малая, а ее произведение на -2 есть также бесконечно малая величина.
Задача 15.19
Найти  . Когда
. Когда  , выражение, стоящее в скобках, есть разность двух бесконечно больших величин, о которой без специального исследования нельзя сказать ничего определенного. Умножим и раздели функцию, стоящую под знаком предела, на выражение, сопряженное с
, выражение, стоящее в скобках, есть разность двух бесконечно больших величин, о которой без специального исследования нельзя сказать ничего определенного. Умножим и раздели функцию, стоящую под знаком предела, на выражение, сопряженное с  , т.е. на
, т.е. на  , и получим
, и получим 
Так как  .
.
Теперь рассмотрим случай, когда  .Выражение, стоящее в скобках, имеет в этом случае положительное значение и неограниченно возрастает по абсолютной величине, множитель же
.Выражение, стоящее в скобках, имеет в этом случае положительное значение и неограниченно возрастает по абсолютной величине, множитель же  , стоящий за скобкой, неограниченно возрастает по абсолютной величине, но сохраняет отрицательное значение Поэтому все выражение
, стоящий за скобкой, неограниченно возрастает по абсолютной величине, но сохраняет отрицательное значение Поэтому все выражение  при
при  неограниченно возрастает по абсолютной величине, сохраняя отрицательное значение и
неограниченно возрастает по абсолютной величине, сохраняя отрицательное значение и  .
.
Задача 15.20
(для самостоятельного решения). Найти 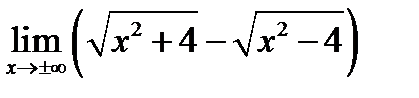 .
.
Ответ.
При  и при
и при  искомый предел равен 0.
искомый предел равен 0.
Задача 15.21
Найти 
Решение.
1) Рассмотрим сначала случай  :
:

Так как 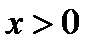 при
при  , а мы рассматриваем арифметическое значение корня, то
, а мы рассматриваем арифметическое значение корня, то  и
и  , а потому
, а потому 
2) Пусть 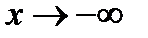 . По-прежнему
. По-прежнему 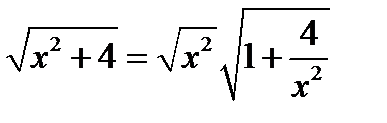 , но теперь
, но теперь  , так как
, так как  , а мы рассматриваем арифметическое значение корня, и
, а мы рассматриваем арифметическое значение корня, и  , а
, а 
Задача 15.22
(для самостоятельного решения). Найти 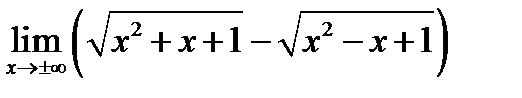 .
.
Указание. Учесть, что при  имеем
имеем 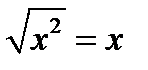 , а при
, а при 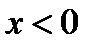 тот же
тот же  .
.
Ответ.
При  искомый предел равен +1, а при
искомый предел равен +1, а при 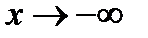 искомый редел равен -1.
искомый редел равен -1.
Задача 15.23
(для самостоятельного решения). Найти  .
.
Ответ.
 при
при  ;
;  при
при 
Задача 15.24
(для самостоятельного решения). Найти  .
.
Указание. Выражение, состоящее под знаком предела, умножить и разделить на  , чтобы получить в числителе разность кубов. После упрощений под знаком предела будет находится выражение
, чтобы получить в числителе разность кубов. После упрощений под знаком предела будет находится выражение
 .
.
Знаменатель дроби представить в виде

И сократить дробь на 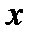 .
.
Ответ 0.
Задача 15.25
(для самостоятельного решения). Найти  .
.
Указание. Выражение, стоящее под знаком предела, умножить и разделить на 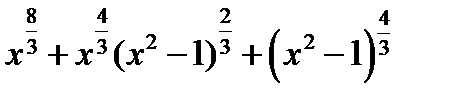 и полученную дробь сократить на
и полученную дробь сократить на  .
.
Ответ. 0.
ШЕСНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Определение пределов тригонометрических функций и упражнения на использование предела  .
.






