Ели функция рассматривается только при целых и положительных значениях аргумента, то она называется функцией натурального аргумента. Множество ее значений образует числовую последовательность: каждому целому предложенному числу соответствует число 
—член последовательности, имеющий номер 
. Это значит, что 
.
Определение. Числовой последовательностью называется множество значений функции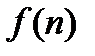 
, определенной на множестве натуральных чисел.
Член 
называется общим членом последовательности.
Последовательность с общим членом 
содержит бесконечное множество чисел и обозначается 
.
Последовательность считается заданной, если дан способ вычисления любого ее члена по известному номеру.
Задача 10.1
Зная общий член последовательности 
написать ее первые десять членов.
Решение.
Давая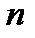 
значения 
получим:
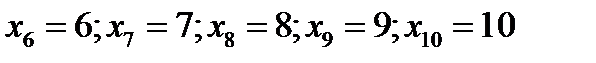
Эта последовательность из 10 членов запишется так 1,2,3,4,5,6,7,8,9,10.
Вообще же последовательность с общим членом 
запишется так: 
Задача 10.2
Написать первые десять членов последовательности, если ее общий член 
.
Решение.
Вычисляя значение дроби 
при значениях 
равных , получим:
.
Вообще же последовательность с общим членом 
запишется так:
Задача 10.3
(для самостоятельного решения). Написать последовательности с общими членами:
1) 
;
2) 
;
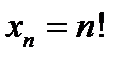3) 
;
4) 
;
5) 
;
6) 
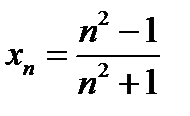
7) 
;
8) 
;
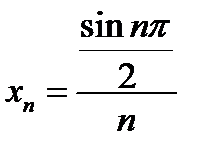9) 
10) 
.
Задача 10.4
По данным первым членам последовательности
Написать ее общий член.
Решение.
Прежде всего отметим, что заданием нескольких первых членов последовательности не определяется вся последовательность. Однако условимся считать, что как написанные члены последовательности, так и все следующие за ними составлены по одному и тому же закону соответствия между натуральными числами и членами последовательности.
В нашем случае нетрудно усмотреть, что числитель каждой дроби равен квадрату номера плюс пять, т.е. 
, а знаменатель каждой дроби на единицу больше числителя, т.е. равен 
. Итак,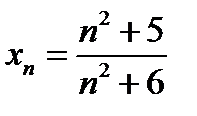 
.
Задача 10.5
(для самостоятельного решения). Написать формулу общего члена последовательности по данным ее первым членам:
1) 
;
2) 
3) 
4) 
5) 
6) 
7) 
Ответ.
1) 
;
2) 
;
3) 
;
4) 
;
5) 
;
6) 
;
7) 
.
Монотонные последовательности
Последовательность называется монотонно возрастающей, если при всех 
каждый ее член больше предыдущего, т.е. если 
, и монотонно убывающей, если каждый ее член меньше предыдущего, т.е. если 
.
Примеры монотонных последовательностей:
1) Последовательность натуральных чисел
—монотонно возрастающая.
2) Последовательность чисел 
, обратных натуральных,
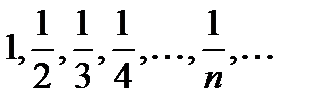—монотонно убывающая.
Если переменная величина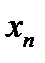 
изменяется не монотонно, то ее называют колеблющейся.
