Течение потоков в реальных элементах самолетов, двигателей и других
конструкций всегда происходит с трением (диссипацией энергии) и часто с энергообменом с окружающей средой. Возможен также отбор или подвод газа. Рассмотрим течение идеального газа в канале при наличии таких воздействий на поток и выведем уравнение, учитывающее их влияние на скорость потока.
Течение газа в канале при принятых выше допущениях описывается следующей системой уравнений:
1) уравнением неразрывности
;
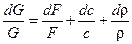2) уравнением сохранения энергии
;
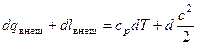3) обобщенным уравнением Бернулли
= 
.
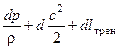Если газ идеальный, то в эту систему входит также уравнение его состояния (в дифференциальной форме)
.
Определив из уравнения (2) 
, а из уравнения (3) - 
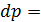
и подставив полученные выражения в уравнение состояния, получим
.
Откуда 
.
Подставляя значение 
в уравнение (1) с учетом того, что
, a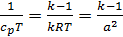 
,
после алгебраических преобразований получим следующее уравнение
. (5.3)
Это уравнение позволяет качественно проанализировать, каким образом различные воздействия влияют на скорость дозвукового и сверхзвукового потока. Здесь рассмотрим лишь некоторые из них.
Тепловое воздействие. В этом случае dq внеш ¹ 0, а dF = dl внеш = dl трен = dG = 0 и общее уравнение примет вид:
.
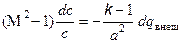Из этого уравнения следует, что подвод теплоты (dq внеш > 0 ) к дозвуковому потоку газа (М < 1) вызывает рост его скорости, а для увеличения скорости сверхзвукового потока (М > 1) теплота должна отводиться (dq внеш < 0).
Утверждение о необходимости изменения знака воздействия при переходе через скорость звука носит название закона обращения воздействия.
Канал, в котором разгон потока происходит под действием подвода или отвода теплоты, называется тепловым соплом.
Воздействие трения. В этом случае dl трен ¹ 0, а dF = dq внеш = = dl внеш = dG = 0 и общее уравнение принимает вид:
.
В отличие от других воздействий работа трения может быть только положительной (dl трен > 0). Поэтому наличие трения при отсутствии других воздействий приводит к разгону дозвукового потока. Это связано с тем, что работа трения переходит в теплоту, а как было показано ранее, подвод теплоты к дозвуковому потоку разгоняет его. Однако следует иметь в виду, что разгон потока под воздействием трения (dc > 0) сопровождается в соответствии с уравнением Бернулли 
уменьшением давления (dp < 0). Это снижение давления будет происходить в большей степени, чем при аналогичном разгоне потока без трения за счет других воздействий (например, геометрического), что объясняется диссипацией энергии в потоке с трением и проявляется в уменьшении полного давления газа р* вдоль канала.
Геометрическое воздействие на течение газа в каналах будет рассмотрено ниже.
