Примечания. 1. Из формулы (2.17) следует, что 
.
Следовательно, газовая постоянная 
представляет собой работу, совершаемую газом в процессе изобарного расширения при его нагреве на 1 градус.
2. Подставим в уравнение первого закона термодинамики 
значения 
, 
и 
в изобарном процессе
.
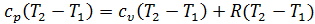Отсюда следует уравнение Майера 
3. Формулу первого закона термодинамики для изобарного процесса независимо от природы газа можно записать в виде
или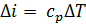 
.
Следовательно, в изобарном процессе теплота процесса численно равна изменению энтальпии рабочего тела.
Изотермический процесс
Изотермическим называется процесс, протекающий при постоянной температуре.
|
|
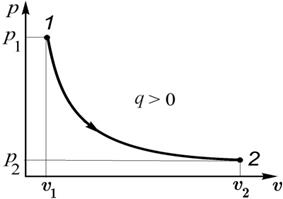
| Рис. 2.7. График изотермического процесса | Рис. 2.8. К определению внутренней энергии газа |
1. Уравнение процесса – 
.
2. График процесса. Из уравнения состояния следует, что 
, так как 
. Следовательно, графиком процесса в р, υ - координатах является равнобокая гипербола (рис. 2.7).
3. Связь между параметрами состояния газа. Для этого запишем уравнение состояния для точек 2 и 1 и разделим их друг на друга
, 
.
Так как в изотермическом процессе 
, то
. (2.20)
4. Теплоемкость газа в изотермическом процессе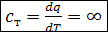 
, так как в этом процессе 
, а 
.
5. Определение количества теплоты q, подведенной к газу, совершенной им работы l и изменения его внутренней энергии Δ u:
- изменение внутренней энергии 
, т.к. 
;
- согласно первому закону термодинамики . Так как = 0, то 
, где 
. Из уравнения состояния следует, что 
. Тогда 
. Таким образом, в изотермическом процессе
. (2.21)
Если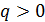 
, то, согласно равенству (2.21), 
. Значит, при подводе теплоты к газу его удельный объем возрастает и наоборот (рис. 2.7).
Таким образом, в изотермическом процессе теплота, сообщаемая газу, идет на совершение им работы расширения против внешних сил.
Используя график изотермического процесса (рис. 2.8), можно показать, что изменение внутренней энергии газа в любом процессе 
. Действительно, во всех процессах a, b и c, начинающихся в точке 0 и заканчивающихся на изотерме, изменение внутренней энергии будет одинаково, т.е. 
, так как начальное и конечное значение температуры в этих процессах одно и то же.
Но согласно первому закону термодинамики в изохорном процессе a теплота, подведенная к газу, идет только на увеличение его внутренней энергии, т.к. в этом процессе газ не совершает работу, т.е. 
. Как установлено выше, в изохорном процессе 
. Отсюда следует, что в любом процессе
.
|
| Рис. 2.9. Графики адиабатного и изотермического процессов |
Адиабатный процесс
Адиабатным называется процесс, протекающий при отсутствии теплообмена с окружающей средой (т.е. при q = 0).
1. Уравнение процесса.
Для вывода уравнения процесса запишем уравнение первого закона термодинамики в двух формах:
и 
или в виде 
и 
.
Разделив второе уравнение на первое, получим
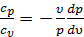или 
,
где 
– показатель адиабаты.
Проинтегрировав последнее уравнение, получим
или 
.
Откуда следует выражение для уравнения адиабатного процесса в виде
. (2.22) 2. График процесса. Из уравнения процесса (2.22) следует, что 
. В р, υ - координатах – это неравнобокая гипебла.
Так как k >1, то адиабата протекает круче изотермы (рис. 2.9).
3. Связь между параметрами состояния газа. Для этого запишем уравнение адиабаты для точек 2 и 1 и разделим их друг на друга
, 
.
Тогда получим
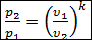. (2.23)
Из уравнения состояния, записанного для точек 1 и 2 (рис. 2.9), следует, что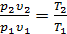 
. Используя соотношение (2.23), получим
. (2.24)
4. Теплоемкость газа в адиабатном процессе. Так как в этом процессе 
, а 
, то
.
5. Определение количества теплоты q, подведенной к газу, совершенной им работы l и изменения его внутренней энергии Δ u:
- количество тепла, подведенного к газу 
;
- изменение внутренней энергии газа
;
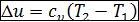- для адиабатного процесса по определению q = 0. Тогда из первого закона термодинамики следует, что при q = 0 работа расширения газа
, (2.25)
т. е. в адиабатном процессе работа газа совершается за счет убыли его внутренней энергии. Поэтому, как видно из формулы (2.25), адиабатное расширение газа (т.е. при 
сопровождается уменьшением его температуры, а сжатие - повышением.
Из уравнения Майера 
и выражения для показателя адиабаты следует, что 
, a 
, тогда
. (2.26)
Политропные процессы
1. К политропным относятся процессы, подчиняющиеся уравнению
, (2.27)
где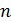 
– показатель политропы, который может принимать значения ±∞. Для данного политропного процесса величина 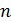постоянная.
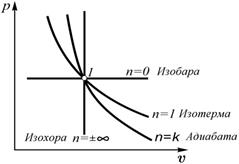
2. Графики политропных процессов. Политропный процесс является обобщающим по отношению к основным термодинамическим процессам. Действительно:
- если 
, то из уравнения политропного процесса получим уравнение изобарного процесса, т.к.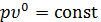 
или 
;
|
| Рис. 2.10. График политропных процессов |
- если 
, тогда 
. Из уравнения состояния следует, что 
. Следовательно, значению соответствует уравнение изотермического процесса ;
если 
, то из уравнения политропного процесса получим уравнение адиабатного процесса 
;
- если 
, то из уравнения политропного процесса 
получим 
– т.е. уравнение изохорного процесса.
3. Связь между параметрами состояния газа в политропном процессе аналогичны связи в адиабатном процессе, а именно
, 
.
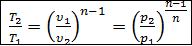4. Определение количества теплоты q, подведенной к газу, совершенной им работы l и изменения его внутренней энергии Δ u: По аналогии с адиабатным процессом:
- количество тепла, подведенного к газу 
;
- изменение внутренней энергии газа ;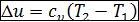
- работа газа в политропном процессе
,
5. Теплоемкость политропного процесса. Подставляя значения q, 
и в уравнение первого закона термодинамики , получим
или 
.
Окончательно для политропного процесса теплоемкость газа равна
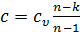. (2.28)
Таким образом, теплоемкость политропного процесса зависит от показателя политропы 
и рода газа, т.к. 
и 
зависят от рода газа.
Теплоемкость в каждом политропном процессе имеет вполне определенную величину, зависящую от значений 
, k и 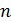. Причем, в зависимости от показателя политропы, теплоемкость может быть положительной или отрицательной, а в отдельных случаях равной нулю (в адиабатном процессе) или бесконечности (в изотермическом процессе). Действительно, в соответствии с (2.28):
- в изобарном процессе , тогда 
;
- в изотермическом процессе → 
;
- в адиабатном процессе → 
;
- в изохорном процессе 
→ 
.
