Задачами исследования термодинамических процессов в газах является выявление закономерностей изменения параметров при протекании процессов и установление закономерностей превращения энергии, т.е. определение значения теплоты 
, работы l и изменения внутренней энергии Δ u.
Методика исследования процессов в газах предусматривает решение следующих вопросов:
1. Установление уравнения процесса;
2. Определение графика процесса;
3. Нахождение связи между параметрами состояния газа, изменяющимися при протекании процесса;
4. Определение теплоемкости газа;
5. Определение количества теплоты q, подведенной к газу, совершенной
им работы l и изменения его внутренней энергии Δ u.
Будем рассматривать только равновесные процессы в идеальных газах.
Изохорный процесс
Изохорным называется процесс, протекающий при постоянном объеме.
1. Уравнение процесса – 
.
2. График процесса – вертикальная линия в р, υ -координатах (рис. 2.5).
3. Связь между параметрами состояния газа. Для этого запишем уравнение состояния для точек 2 и 1 и разделим их друг на друга
, 
.
Так как в изохорном процессе 
, то
. (2.14)
4. Теплоемкость газа в изохорном процессе обозначается символом 
. Для идеального газа при умеренных температурах
где 
– число степеней свободы молекулы газа.
|
| Рис. 2.5. График изохорного процесса |
5. Определение количества теплоты q, подведенной к газу, совершенной им работы l и изменения его внутренней энергии Δ u:
- так как 
, то 
, значит, элементарная работа 
и работа расширения газа l = 0;
- согласно первому закону термодинамики 
. Так как l = 0, то
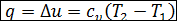. (2.15).
Если 
, то 
. Тогда из (2.14) следует, что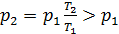 
. Значит, при подводе теплоты к газу его давление возрастает и наоборот (рис. 2.5).
Таким образом, в изохорном процессе теплота, сообщаемая газу, идет только на увеличение его внутренней энергии, т.е. на увеличение его температуры.
Изобарный процесс
Изобарным называется процесс, протекающий при постоянном дав-
Лении.
1. Уравнение процесса – 
.
2. График процесса – горизонтальная линия в р, υ -координатах (рис. 2.6).
3. Связь между параметрами состояния газа. Для этого запишем уравнение состояния для точек 2 и 1 и разделим их друг на друга
, .
|
| Рис. 2.6. График изобарного процесса |
Так как в избарном процессе 
, то
. (2.16)
4. Теплоемкость газа в изобарном процессе обозначается символом ср. Для идеального газа при умеренных температурах
.
5. Определение количества теплоты q, подведенной к газу, совершенной им работы l и изменения его внутренней энергии Δ u:
— работа расширения газа: так как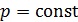 
, то
(2.17)
— количество тепла, подведенного к газу
; (2.18)
— изменение внутренней энергии газа
; (2.19)
Если 
, то . Тогда из (2.16) следует, что 
. Значит, при подводе к газу теплоты его удельный объем возрастает и наоборот (рис. 2.6).
