Первый закон термодинамики представляет собой результат обобщения многочисленных наблюдений и экспериментов, утверждающий, что теплота, сообщенная системе в каком-либо процессе, идет на повышение её внутренней энергии и на совершение системой работы против внешних сил.
Таким образом, если в результате взаимодействия с внешней средой термодинамической системе передана теплота Q и при этом система совершила против внешних сил работу L, а её внутренняя энергия возросла на 
, то
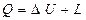. (2.2)
Первый закон термодинамики (2.2) применительно к единице массы рабочего тела может быть записан в виде
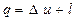(2.3)
или в дифференциальной форме
. (2.4)
Работа и теплота
|
| Рис. 2.2 |
Работа газа. Рассмотрим равновесный процесс расширения газа в цилиндре с поршнем (рис. 2.2). Пусть изменение состояния газа в цилиндре изображается в координатах р, 𝜐 кривой 1 - 2 (рис. 2.3). Газ, расширяясь, совершает работу против внешних сил (действующих со стороны поршня). Если в некотором промежуточном состоянии между точкам 1 и 2 газ имеет давление р, то при бесконечно малом перемещении поршня на расстояние dx работа, совершаемая газом, будет равна:
,
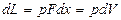где F - площадь поршня, а полная работа, совершаемая газом в процессе 1- 2,
.
В расчете на 1 кг газа его работа в элементарном процессе равна:
, (2.5)
| 
|
| Рис. 2.3 | Рис. 2.4 |
где 
- удельный объем газа, а полная работа в процессе 1-2
, (2.6)
т.е. работа газа эквивалентна площади, расположенной под кривой 1-2 в координатах р, .
Правило знаков для работы и теплоты. Во всех формулах, выражающих первый закон термодинамики, положительными считаются теплота, подведенная к системе (телу) и работа, произведенная самой системой, т.е. отведенная от неё.
С учетом того, что уравнение первого закона термодинамики в дифференциальной форме можно записать так:
,(2.7)
а в интегральной форме 
.
Рассмотрим теперь два разных равновесных процесса перехода тела из состояния 1 в состояние 2 (рис. 2.4). Хотя в процессах а и b исходные и конечные состояния тела одинаковы, значения работы в этих процессах (эквивалентные площадям под кривыми а и b) различны. Таким образом, работа тела (системы) не является функцией состояния, а зависит от характера процесса, в котором она производится.
Теплота. Теплота, также как и работа, не является функцией состояния. Действительно, поскольку работа l зависит от характера протекания данного процесса, а D u не зависит от него, а определяется только начальным и конечным состояниями системы, то, как следует из первого закона термодинамики,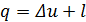 
, теплота также зависит от характера протекания процесса.
В общем случае переменной теплоемкости тела в данном процессе
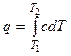. (2.8)
Если же для данного процесса известны значения средней теплоемкости 
, то тогда 
. (2.9)
Энтальпия
В термодинамических расчетах, кроме внутренней энергии, широко используется другая функция состояния - энтальпия. Так называется термодинамическая функция, равная (в расчете на единицу массы):
i = u + p . (2.10)
Энтальпия является функций состояния поскольку u - функция состояния, а p и v - параметры состояния.
В дифференциальной форме
. (2.11)
Определим энтальпию идеального газа. Для идеального газа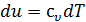 
, а из уравнения состояния идеального газа следует, что 
. Тогда 
.
Но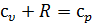 
. Следовательно, для идеального газа
. (2.12)
Первый закон термодинамики в дифференциальной форме имеет вид:
Поскольку из (2.11) следует, что 
, а 
, то уравнение первого закона термодинамики может быть записано также в виде: 
. (2.13)
