Задание 1
Даны вершины А (x 1; y 1), В (x 2; y 2), С (x 3; y 3) треугольника.
Найти:
1. Длину стороны АВ.
2. Угол А.
3. Уравнение медианы, проведенной из вершины С.
4. Координаты точки пересечения высот треугольника.
5. Длину высоты, опущенной из вершины С.
6. Образ точки пересечения высот при осевой симметрии относительно прямой АВ.
7. Уравнение прямой, проходящей через точку пересечения высот, параллельной прямой АВ.
Сделать чертеж.
Задачи 1–10
1. А (0;0), В (6;3), С (3;4).
2. А (0;2), В (6;5), С (3;6).
3. А (–1;0), В (5;3), С (2;4).
4. А (–2;1), В (4;4), С (1;5).
5. А (–2;0), В (4;3), С (1;4).
6. А (–1;2), В (5;5), С (2;6).
7. А (–2;2), В (4;5), С (1;6).
8. А (0;1), В (6;4), С (3;5).
9. А (1;1), В (7;4), С (4;5).
10. А (1;–1), В (7;2), С (4;3).
Задание 2
Найти уравнение линии, если отношение расстояний от каждой ее точки до точки F (a; b) и до прямой Ах + Ву + С = 0 равно  . Сделать чертеж.
. Сделать чертеж.
Задачи 11–20
11. а = 1, b = 0, А = 0, В = 1, С = 3,  = 3.
= 3.
12. а = 2, b = 1, А = 1, В = 0, С = 2,  = 1.
= 1.
13. а = –3, b = 0, А = 1, В = 0, С = 0,  = 2.
= 2. 

14. а = 0, b = –4, А = 0, В = 1, С = 1,  =
=  .
.
15. а = 4, b = 0, А = 1, В = 0, С = 1,  =
=  .
.
16. а = –3, b = 3, А = 0, В = 1, С = –1,  =
=  .
.
17. а = 3, b = –2, А = 0, В = 1, С = –4,  = 1.
= 1.
18. а = –2, b = 0, А = 0, В = 1, С = –3,  =
=  .
.
19. а = 0, b = 3, А = 1, В = 0, С = –4,  =
=  .
.
20. а = 0, b = 1, А = 0, В = 1, С = 3,  =
= 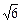 .
.
Задание 3
Даны векторы  и вектор
и вектор  со своими координатами в базисе
со своими координатами в базисе 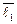 ,
, 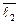 ,
, 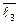 . Показать, что векторы
. Показать, что векторы  сами образуют базис, и найти координаты этого вектора
сами образуют базис, и найти координаты этого вектора  в новом базисе.
в новом базисе.
Задачи 21–30
21.  = (2;–1;2),
= (2;–1;2), 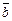 = (3;1;2),
= (3;1;2), 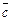 = (0;–1;2),
= (0;–1;2),  = (1;–7;10).
= (1;–7;10).
22.  = (1;3; 0),
= (1;3; 0), 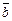 = (2;0;0),
= (2;0;0), 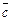 = (1;2;–1),
= (1;2;–1),  = (3;–3; 0).
= (3;–3; 0).
23.  = (4;7;8),
= (4;7;8), 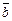 = (9;1;3),
= (9;1;3), 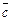 = (2;–4;1),
= (2;–4;1),  = (1;–13;–13).
= (1;–13;–13).
24.  = (2;7;3),
= (2;7;3), 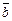 = (3;1;8),
= (3;1;8), 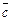 = (2;–7;4),
= (2;–7;4),  = (16;14;27).
= (16;14;27).
25.  = (–3;2;1),
= (–3;2;1), 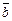 = (4;1;2),
= (4;1;2), 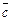 = (1;2;–1),
= (1;2;–1),  = (–3;10;–1).
= (–3;10;–1).
26.  = (2;1;4),
= (2;1;4), 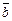 = (–3;5;1),
= (–3;5;1), 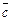 = (1;–4;–3),
= (1;–4;–3),  = (–7;5;–5).
= (–7;5;–5).
27.  = (2;–4;3),
= (2;–4;3), 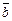 = (1;–2;4),
= (1;–2;4), 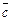 = (3;–1;5),
= (3;–1;5),  = (2;–9;5).
= (2;–9;5).
28.  = (2;3;1),
= (2;3;1), 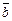 = (–1;2;–2),
= (–1;2;–2), 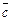 = (1;2;1),
= (1;2;1),  = (9;11;7).
= (9;11;7).
29.  = (1;2;3),
= (1;2;3), 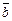 = (2;–1;–1),
= (2;–1;–1), 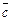 = (1;3;4),
= (1;3;4),  = (4;4;6).
= (4;4;6).
30.  = (1;2;1),
= (1;2;1), 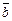 = (–1;0;1),
= (–1;0;1), 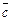 = (2;0;0),
= (2;0;0),  = (4;2;0).
= (4;2;0).
Задание 4
Исследовать на совместность и решить систему уравнений.
Задачи 31–40
31. 
| 36. 
|
32. 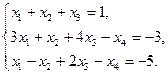
| 37. 
|
33. 
| 38. 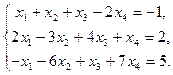
|
34. 
| 39. 
|
35. 
| 40. 
|
Задание 5
Вычислить пределы функций.
Задачи 41–50
41. 1)  при а) х 0 = 3; б) х 0 = –5; в) х 0 = при а) х 0 = 3; б) х 0 = –5; в) х 0 =  ;
2) ;
2)  ; 3) ; 3)  ; 4) ; 4)  . .
|
42. 1)  при а) х 0 = –4; б) х 0 = 1; в) х 0 = при а) х 0 = –4; б) х 0 = 1; в) х 0 =  ;
2) ;
2)  ; 3) ; 3)  ; 4) ; 4) 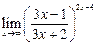 . .
|
43. 1)  при а) х 0 = –6; б) х 0 = 2; в) х 0 = при а) х 0 = –6; б) х 0 = 2; в) х 0 =  ;
2) ;
2) 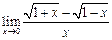 ; 3) ; 3)  ; 4) ; 4)  . .
|
44. 1)  при а) х 0 = 2; б) х 0 = –1; в) х 0 = при а) х 0 = 2; б) х 0 = –1; в) х 0 =  ;
2) ;
2)  ; 3) ; 3)  ; 4) ; 4)  . .
|
45. 1)  при а) х 0 = –1; б) х 0 = –2; в) х 0 = при а) х 0 = –1; б) х 0 = –2; в) х 0 =  ;
2) ;
2)  ; 3) ; 3)  ; 4) ; 4)  . .
|
46. 1)  при а) х 0 = –1; б) х 0 = –4; в) х 0 = при а) х 0 = –1; б) х 0 = –4; в) х 0 =  ;
2) ;
2)  ; 3) ; 3)  ;4) ;4) 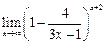 . .
|
47. 1)  при а) х 0 = –4; б) х 0 = 2; в) х 0 = при а) х 0 = –4; б) х 0 = 2; в) х 0 =  ;
2) ;
2)  ; 3) ; 3)  ; 4) ; 4) 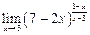 . .
|
48. 1)  при а) х 0 = –3; б) х 0 = –1; в) х 0 = при а) х 0 = –3; б) х 0 = –1; в) х 0 =  ;
2) ;
2)  ; 3) ; 3)  ; 4) ; 4)  . .
|
49. 1)  при а) х 0 = –3; б) х 0 = –2; в) х 0 = при а) х 0 = –3; б) х 0 = –2; в) х 0 =  ;
2) ;
2)  ; 3) ; 3)  ; 4) ; 4) 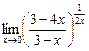 . .
|
50. 1)  при а) х 0 = –9; б) х 0 = –1; в) х 0 = при а) х 0 = –9; б) х 0 = –1; в) х 0 =  ;
2) ;
2)  ; 3) ; 3)  ; 4) ; 4)  . .
|
Задание 6
Найти производные функций.
Задачи 51–60
51. 1) y = sin (ex + 1) · ln x;
2) y = arctg (ex + 5 x);
3) y = (x 2 + x)10 · tg3 x.
52. 1) y = tg (ln x – 2) · e 2 x ;
2) y = arcsin 2(ex – x);
3) y = (sin 2 x + 3)10 · x 2.
53. 1) y = ctg ( – 1) · sin x;
2) y = arccos 3(ex – 3);
3) y = (tg 3 x + 4)12 · x 3.
54. 1) y = – 1) · sin x;
2) y = arccos 3(ex – 3);
3) y = (tg 3 x + 4)12 · x 3.
54. 1) y =  ;
2) y = ;
2) y =  ;
3) ;
3)  .
55. 1) .
55. 1)  ;
2) ;
2)  ;
3) ;
3)  . .
| 56. 1)  ;
2) y = arcctg 3(ex – 2) · x;
3) ;
2) y = arcctg 3(ex – 2) · x;
3)  .
57. 1) .
57. 1)  ;
2) y = ;
2) y =  ;
3) ;
3)  .
58. 1) y = tg 9 x – x 2 · .
58. 1) y = tg 9 x – x 2 · 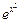 ;
2) ;
2)  ;
3) ;
3) 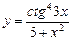 .
59. 1) .
59. 1)  ;
2) ;
2)  ;
3) ;
3)  .
60. 1) y = (sin 5 x + e 2 x )4;
2) .
60. 1) y = (sin 5 x + e 2 x )4;
2)  ;
3) ;
3)  . .
|
Задание 7
Исследовать средствами дифференциального исчисления функцию и построить ее график.
Задачи 61–70
61.  ;
62. ;
62.  ;
63. ;
63.  ;
64. ;
64.  ;
65. ;
65.  ; ;
| 66.  ;
67. ;
67. 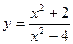 ;
68. ;
68. 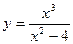 ;
69. ;
69.  ;
70. ;
70.  . .
|

ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ № 2
Задание 1
Показать, что данная функция удовлетворяет указанному соотношению.
Задачи 1–10
1. u =  ,
,  .
.
2.  ,
,  .
.
3.  ,
, 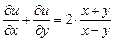 .
.
4.  ,
,  .
.
5.  ,
,  .
.
6. 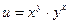 ,
,  .
.
7.  ,
,  .
.
8.  ,
,  .
.
9.  ,
,  .
.
10. u = y · sin (y · e–x),  .
.
Задание 2
Найти неопределeнные интегралы. Результаты проверить дифференцированием.
Задачи 11–20
11. 1)  ;
2) ;
2)  ;
3) ;
3)  .
12. 1) .
12. 1)  ;
2) ;
2)  ;
3) ;
3)  .
13. 1) .
13. 1)  ;
2) ;
2)  ;
3) ;
3)  .
14. 1) .
14. 1)  ;
2) ;
2)  ;
3) ;
3)  .
15. 1) .
15. 1) 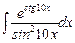 ;
2) ;
2)  ;
3) ;
3) 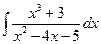 . .
| 16. 1)  ;
2) ;
2)  ;
3) ;
3) 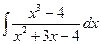 .
17. 1) .
17. 1)  ;
2) ;
2) 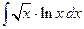 ;
3) ;
3) 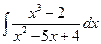 .
18. 1) .
18. 1) 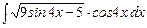 ;
2) ;
2)  ;
3) ;
3)  .
19. 1) .
19. 1)  ;
2) ;
2)  ;
3) ;
3)  .
20. 1) .
20. 1)  ;
2) ;
2)  ;
3) ;
3)  . .
|
Задание 3
Найти площади плоских фигур, заключенных между линиями.
Задачи 21–30
21. y = sin 2 x, y = 0,  .
.
22. y = cos 0,5 x, y = 0,  .
.
23.  , y = x, x = 2, y = 0.
, y = x, x = 2, y = 0.
24.  ,
,  ,
, 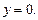
25. y = ex, y = e, x = 0.
26. y = 2 cos x, y = 0,  .
.
27. y = 2 sin x, y = 0, 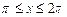 .
.
28. y = 3 x 2, y = 1,5 x + 4,5, y = 0.
29.  ,
,  .
.
30.  ,
,  ,
,  .
.
Задание 4
Найти область сходимости степенного ряда  .
. 
Задачи 31–40
31.  . .
| 35. 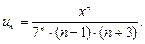
|
32. 
| 36. 
|
33. 
| 37. 
|
34. 
| 38. 
|
39. 
| 40.  . .
|
Задание 5
Вычислить определенный интеграл с точностью до 0,001 с помощью разложения подынтегральной функции в ряд по степеням х
и последующего почленного интегрирования.
Задачи 41–50
| 41. |  . .
| 46. |  . .
|
| 42. |  . .
| 47. | 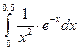 . .
|
| 43. |  . .
| 48. |  . .
|
| 44. |  . .
| 49. | 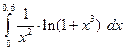 . .
|
| 45. |  . .
| 50. |  . .
|
Задание 6
Решить задачу Коши для линейного неоднородного дифференциального уравнения первого порядка.
Задачи 51–60
51.  , y (1) =
, y (1) =  .
.
52.  , y (0) = 1.
, y (0) = 1.
53.  , y (0) = 2.
, y (0) = 2.
54. 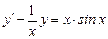 ,
,  .
.
55.  , y (1) = e.
, y (1) = e.
56. 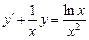 , y (1) = – 5.
, y (1) = – 5.
57. 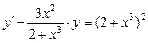 , y (0) = 6.
, y (0) = 6.
58.  , y (0) = –3.
, y (0) = –3.
59.  ,
, 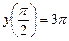 .
.
60.  , y (0) = 7.
, y (0) = 7.
Задание 7
Найти общее решение линейного неоднородного дифференциального уравнения второго порядка.
Задачи 61–70
| 61. | y'' – 6 y' + 5 y = 2 x 2 + x. |
| 62. | y'' + 4 y' + 4 y = 3 sin x. |
| 63. | y'' – 4 y' + 5 y = 4 · e 3 x . |
| 64. | y'' – 5 y' = x 2. |
| 65. | y'' – 3 y' – 10 y = –2 · e 5 x . |
| 66. | y'' – 6 y' + 9 y = –7 · e 3 x . |
| 67. | y'' – 2 y' + 10 y = –5 x 2. |
| 68. | y'' + 5 y' = 7 · e 2 x . |
| 69. | y'' + 10 y' + 25 y = x 2 – 3 x + 5. |
| 70. | y'' – 4 y' – 21 y = sin x + cos x. |
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Шипачев В. С. Задачи по высшей математике: Учебное пособие для вузов. — М.: Высшая школа, 1997. — 304 с.
Сборник индивидуальных учебных заданий по высшей математике: Учебное пособие: В 3 ч. Ч. 1 / А. П. Рябушко, В. В. Бархатов,
В. В. Державец, И. Е. Юруть; Под общ. ред. А. П. Рябушко. — Мн.: Вышэйшая школа, 1990. — 270 с.
Лихолетов И. И. Высшая математика, теория вероятностей и математическая статистика. — Мн.: Вышэйшая школа, 1976. — 720 с.
Шипачев В. С. Основы высшей математики: Учебное пособие для вузов / Под ред. А. Н. Тихонова. — 3-е изд., стер. — М.: Высшая школа, 1998. — 479 с.
Минюк С. А., Ровба Е. А. Высшая математика: Учебное пособие для студентов экономических специальностей высших учебных заведений. — Гродно: Гродненский государственный университет, 2000. — 394 с.
Сборник задач и упражнений по высшей математике. Общий курс: Учебное пособие / А. В. Кузнецов, Д. С. Кузнецова, Е. И. Шилкина
и др. — Мн.: Вышэйшая школа, 1994. — 284 с.
Лихолетов И. И., Мацкевич И. П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. — 3-е изд., стер. — Мн.: Вышэйшая школа, 1976. — 456 с.
Высшая математика. Общий курс: Учебник / А. И. Яблонский,
А. В. Кузнецов, Е. И. Шилкина и др.; Под общ. ред. С. А. Самаля. —Мн.: Вышэйшая школа, 2000. — 351 с.
Гусак А. А. и др. Справочник по высшей математике / А. А. Гусак, Г. М. Гусак, Е. А. Бричикова. — Мн.: ТетраСистемс, 1999. — 640 с.
Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики: Учебное пособие для вузов. — 7-е изд., испр. — М.: Наука, 1989. — 656 с.
Гусак А. А. Задачи и упражнения по высшей математике: В 2 ч. Ч. 1. — 2-е изд., перераб. — Мн.: Вышэйшая школа, 1988. — 247 с.
Данко П. Е. и др.Высшая математика в упражнениях и задачах:
В 2 ч. Ч. 1 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. — 5-е изд., испр. — М.: Высшая школа, 1999. — 304 с.
Минорский В. П. Сборник задач по высшей математике: Учебное пособие для вузов. — 13-е изд., стер. — М.: Наука, 1987. — 352 с.
Высшая математика. Общий курс: Учебник / А. В. Кузнецов,
Л. Ф. Янчук, С. А. Мызгаева и др.; Под общ. ред. А. И. Яблонского. — Мн.: Вышэйшая школа, 1993. — 349 с.
Жевняк Р. М. и др. Общий курс высшей математики: Учебное пособие для экономических специальностей вузов / Р. М. Жевняк,
А. А. Карпук, А. И. Марченко, В. Т. Унукович. — Орша, 1996. — 320 с.
Красс М. С. Математика для экономических специальностей: Учебник. — М.: Инфра-М, 1999. — 464 с.
Гусак А. А. Высшая математика: В 2 т. Т. 1. — 2-е изд., испр. — Мн.: ТетраСистемс, 2000. — 544 с.
СОДЕРЖАНИЕ
Пояснительная записка..................................................................... 3
Программа курса.............................................................................. 4
Методические указания по выполнению заданий
контрольной работы № 1.................................................................. 8
Методические указания по выполнению заданий
контрольной работы № 2................................................................ 52
Требования к оформлению контрольных работ............................ 85
Варианты контрольной работы № 1............................................... 87
Варианты контрольной работы № 2............................................... 89
Задания контрольной работы № 1.................................................. 91
Задания контрольной работы № 2.................................................. 97
Список рекомендуемой литературы............................................ 102
Учебное издание
ВЫСШАЯ МАТЕМАТИКА
ОБЩИЙ КУРС
Пособие
(программа курса, задания контрольных работ № 1 и № 2
и методические рекомендации по их выполнению)
для студентов первого курса заочной формы обучения
специальностей «Коммерческая деятельность»,
«Товароведение и экспертиза товаров», «Маркетинг»
Авторы-составители:
Кохно Александр Павлович
Романенко Николай Денисович
Мокеева Светлана Александровна
Кузменкова Инна Анатольевна
| Редактор | О. М. Ковалева |
| Компьютерная верстка | И. Г. Лейковская |
Подписано в печать 25.11.02.Формат 60´841/16.
Бумага типографская № 1. Гарнитура Таймс.
Усл. печ. л. 6,04. Уч.-изд. л. 6,0. Тираж 625 экз. Заказ №
УО «Белорусский торгово-экономический университет
потребительской кооперации».
Лицензия ЛВ № 111 от 21.01.02.
246029, г. Гомель, просп. Октября, 50.
Отпечатано на ризографе
УО «Белорусский торгово-экономический университет
потребительской кооперации».
Лицензия ЛП № 112 от 10.01.02.
 |
246029, г. Гомель, просп. Октября, 50.






