Понятие неопределенного интеграла
Функция F (x) называется первообразной для функции f (x) на некотором промежутке Х, если для любого элемента 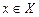 выполняется равенство F' (x) = f (x).
выполняется равенство F' (x) = f (x).
Если F (x) — одна из первообразных для функции f (x) на промежутке Х, то всякую другую первообразную Ф (х) на промежутке Х можно представить в виде Ф (х) = F (x) + с, где с — постоянная величина.
Неопределенным интегралом от функции f (x) называется множество всех ее первообразных, т. е. 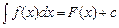 .
.
При этом f (x) — подынтегральная функция, f (x) dx — подынтегральное выражение, 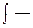 знак неопределенного интеграла, х —
знак неопределенного интеграла, х —
переменная интегрирования.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Свойства неопределенного интеграла:
1. 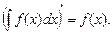
2. 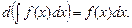
3. 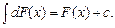
4. 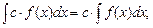 где с — постоянная величина.
где с — постоянная величина.
5. 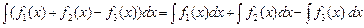 .
.
6. Если 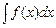 = F (x) + c и
= F (x) + c и 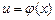 — дифференцируемая функция, то
— дифференцируемая функция, то 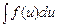 = F (и) + c.
= F (и) + c.
Таблица основных неопределенных интегралов:
1. 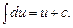
2. 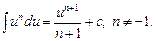
3. 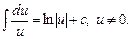
4. 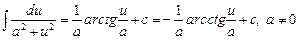 .
.
5. 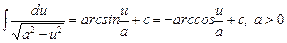 .
.
6. 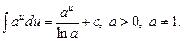
7. 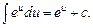
8. 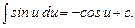
9. 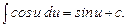
10. 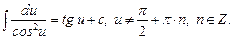
11. 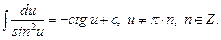
12. 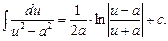
13. 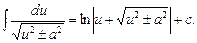
14. 
15. 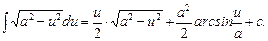
16. 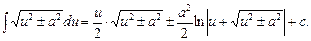
Интегрирование методом замены переменной и по частям
Метод замены переменной проводится по формуле
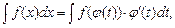
где х = 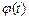 — некоторая дифференцируемая функция.
— некоторая дифференцируемая функция.
Если и = и (х), v = v (x) — некоторые дифференцируемые функции, то справедлива формула интегрирования по частям
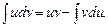
Интегрирование простейших рациональных дробей
Интегрирование проводят в зависимости от типа простейшей рациональной дроби.
1. 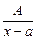 (А, а — постоянные действительные числа) — простейшая рациональная дробь первого типа.
(А, а — постоянные действительные числа) — простейшая рациональная дробь первого типа.
Пример. 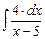 =
= 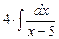 =
= 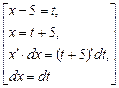 =
=  = =
= = 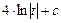 =
= 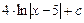 .
.
2. 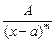 (А, а, т — постоянные числа,
(А, а, т — постоянные числа, 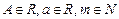 ,
, 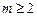 ) — простейшая рациональная дробь второго типа.
) — простейшая рациональная дробь второго типа.
Пример. 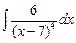 =
= 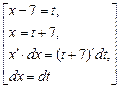 =
= 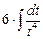 =
= 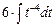 =
=
= 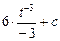 =
= 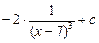 =
= 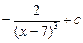 .
.
3. 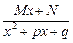 (М, N, p, q — постоянные числа, М, N, p, q
(М, N, p, q — постоянные числа, М, N, p, q 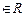 , х 2 + рх + q не имеет действительных корней) — простейшая рациональная дробь третьего типа.
, х 2 + рх + q не имеет действительных корней) — простейшая рациональная дробь третьего типа.
Пример. 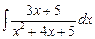 =
= 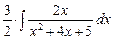 +
+ 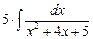 =
=
= 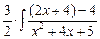 dx +
dx + 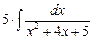 =
= 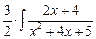 dx –
dx – 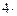
 ·
·
· 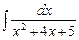 + 5 ·
+ 5 · 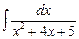 =
= 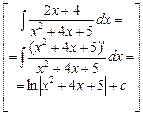 =
=
= 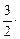
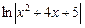 –
– 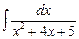 =
= 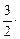
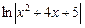 –
– 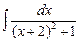 =
=
=[ d (x + 2) = (x + 2) 'dx = dx ] = 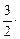
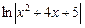 –
– 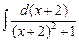 =
=  ·
·
· 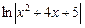 – arctg (x + 2) + c.
– arctg (x + 2) + c.
4. 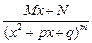 (М, N, р, q — постоянные числа, М, N, р, q
(М, N, р, q — постоянные числа, М, N, р, q 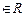 ,
, 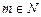 ,
, 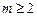 ; х 2 + рх + q не имеет действительных корней) — простейшая рациональная дробь четвертого типа.
; х 2 + рх + q не имеет действительных корней) — простейшая рациональная дробь четвертого типа.
Интеграл от этой дроби считается с помощью рекуррентных формул, позволяющих уменьшить число т до 1.
Интегрирование правильных и неправильных рациональных дробей
Рациональная дробь 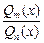 (Qn (x), Qm (x) — некоторые многочлены степеней n и m соответственно) называется правильной, если
(Qn (x), Qm (x) — некоторые многочлены степеней n и m соответственно) называется правильной, если  , и неправильной в противном случае (если
, и неправильной в противном случае (если 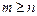 ).
).
Для интегрирования правильной дроби ее предварительно раскладывают на простейшие дроби. Для этого многочлен Qn (x) разлагают на неприводимые множители. Общий вид такого разложения следующий:
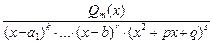 =
= 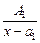 +
+ 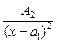 + … +
+ … +
+ 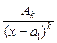 + … +
+ … +  + … +
+ … + 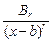 +
+ 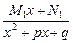 +
+
+ 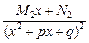 +…+
+…+ 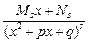 ,
,
где А 1, А 2, …, Аk, В 1, В 2, …, Вr , М 1, М 2, …, Мs , N 1, N 2, …, Ns — некоторые неопределенные действительные коэффициенты, которые следует еще определить.
Интегрирование неправильной рациональной дроби сводят к интегрированию правильной рациональной дроби выделением из первой целой части.






