При исследовании функций и построении графиков рекомендуется использовать нижеприведенную схему.
1. Указать область определения функции D (y).
2. Исследовать функцию на четность, нечетность.
Функция y = f (x) с симметричной относительно начала координат областью определения D (y) называется четной, если для всех х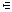 
D (y) выполняется равенство f (– x) = f (x), и нечетной, если f (– x) = –f (x). График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат.
3. Провести исследование функции на периодичность.
Если функция периодическая, то дальнейшее исследование можно проводить на интервале, длина которого равна периоду.
4. Исследовать поведение функции на границе области опре-
деления, найти односторонние пределы в точках разрыва. Найти асимптоты.
Прямая 
называется асимптотой графика функции y = f (x), если расстояние от точки М графика функции до прямой стремится к нулю при неограниченном удалении этой точки по графику функции от начала координат. Различают вертикальные, наклонные и горизонтальные асимптоты.
Пусть х 0 — точка разрыва функции. Прямая х = х 0 называется вертикальной асимптотой графика функции y = f (x), если хотя бы один из односторонних ее пределов в точке х 0 равен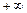 
(или 
).
Если существуют и конечны 
= k, 
, то прямая у = k · x + b называется наклонной асимптотой графика функции y = f (x).
Горизонтальная асимптота — это частный случай наклонной
при k = 0.
5. Найти производную y'.
6. Найти критические точки функции, т. е. те значения аргумента х, которые принадлежат D (y) и в которых производная y' равна нулю или ее не существует.
7. Найти интервалы монотонности и точки локальных экстремумов.
Теорема 1. Если дифференцируемая функция y = f (x), х 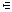(a, b) возрастает (убывает) на интервале (a, b), то 
(
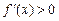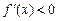) для любого х 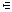(a, b).
Теорема 2. Если функция y = f (x), х 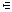(a, b) имеет положительную (отрицательную) производную в каждой точке интервала (a, b), то эта функция возрастает (убывает) на интервале (a, b).
Точка х 0, принадлежащая D (y), называется точкой локального минимума (максимума) функции y = f (x), если найдется такая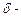 
окрест-
ность (х 0 – 
; х 0 + ) 
точки х 0 (х' 0), что для всех
х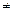 
х 0 (х 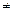х' 0) из этой окрестности (рис. 12) выполняется неравенство
.
Точки локальных минимума и максимума называются точками локального экстремума, а значения функции в этих точках называются локальными экстремумами функции.
Теорема 3. Пусть функция y = f (x) непрерывна в критической точке х 0 и в некоторой 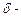окрестности имеет конечную производную, кроме, быть может, самой точки х 0. Если при переходе через точку х 0 производная f' (x) меняет свой знак с плюса на минус, то х 0 является точкой локального максимума, если же f' (x) при переходе через х 0 меняет знак с минуса на плюс, то она является точкой локального минимума.
|
| Рис. 12 |
8. Найти вторую производную 
, т. е. производную от первой производной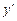 
.
9. Определить интервалы выпуклости, вогнутости графика функции, точки перегиба.
График функции y = f (x) имеет на интервале (a, b) выпуклость (вогнутость), если он расположен ниже (выше) любой касательной, проведенной к нему в любой точке из (a, b) (рис. 13).
|
| Рис. 13 |
Точка графика функции из D (y), в которой выпуклость сменяется вогнутостью (или наоборот), называется точкой перегиба.
Теорема. Если во всех точках интервала (a, b) функция y = f (x) имеет отрицательную (положительную) вторую производную , то график этой функции на интервале (a, b) является выпуклым (вогнутым). Если вторая производная при переходе через точку х 0, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х 0 — точка перегиба.
10. Найти точки пересечения графика с осями координат, интервалы знакопостоянства фукции (промежутки, на которых f (x) > 0 или f (x) < 0), контрольные точки.
11. Построить график функции с учетом проведенного исследования.
Вопросы для самопроверки
1. Дайте определение производной. Каков ее геометрический смысл?
2. Какие вы знаете экономические интерпретации производной функции? Приведите примеры.
3. Пусть функция y = f (x) является в некоторой точке дифференцируемой. Следует ли отсюда, что она является непрерывной в этой точке?
4. Сформулируйте общие правила дифференцирования функций и формулы нахождения производных основных элементарных функций.
5. Что называется дифференциалом функции? По какой формуле он вычисляется?
6. Для раскрытия каких неопределенностей может быть использовано правило Лопиталя? Приведите примеры.
7. Как определяются асимптоты кривой? Каким образом они находятся?
8. Какие вы знаете признаки возрастания и убывания функции? Покажите, что функция у = ln x возрастает, а функция у = cos x – 2 x убывает при всех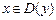 
.
9. Что называется экстремумом функции? Сформулируйте достаточное условие его существования.
10. Дайте определение выпуклости, вогнутости графика функции на интервале. Сформулируйте достаточные условия существования этих свойств у графика.
11. Какая точка называется точкой перегиба графика функции? Какое вы знаете достаточное условие существования перегиба в точке?
12. Какова схема исследования функции и построения ее графика?
Типовая задача 6
Найти производные следующих функций:
1) у = (ln2 x + 5 x)10;
2) у = (5 cos 3 x + x) · tg 3 x;
3) 
.
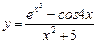Решение. Используя формулы и правила дифференцирования, находим производные данной функции следующим образом:
1) 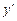= ((ln2 x + 5 x)10) ' = 10 · (ln2 x + 5 x)9 · (ln2 x + 5 x) ' = 10 · (ln2 x +
+ 5 x)9 · 
= 10 · (ln2 x + 5 x)9 · 
.
2) 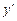=((5 cos 3 x + x) · tg 3 x) ' = (5 cos 3 x + x) ' · tg 3 x + (5 cos 3 x + x) · (tg 3 x) ' =
= (5 cos 3 x · ln5 · (cos 3 x) ' + 1) · tg 3 x + (5 cos 3 x + x) · 
· 3 = (–5 cos 3 x · ln5 · · sin 3 x · 3 + 1) · tg 3 x + (5 cos 3 x + x) · 
= (–3 · ln5 · 5 cos 3 x · sin 3 x +
+ 1) · tg 3 x +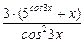 
.
3) 
= 
=
= 
=
= 
.
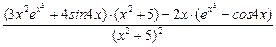Ответ: 1) 10 · (ln2 x + 5 x)9 · ;
2) (–3 · ln5 · 5 cos 3 x · sin 3 x + 1) · tg 3 x + ;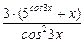
3) .
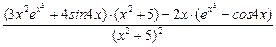Типовая задача 7
Исследовать функцию у = 
и построить ее график.
Решение. 1. Так как функция не определена при х + 1 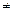0 (х 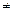–1), то D (y) = 
.
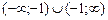2. Функция является ни четной, ни нечетной, так как D (y) не является симметричной относительно начала координат.
3. Функция является непериодической.
4. Находим асимптоты.
х = –1 — точка разрыва. Если х будет стремиться к (–1) слева, оставаясь меньше (–1), то (х + 1)2 — положительная бесконечно малая функция, а — положительная бесконечно большая функция, т. е. если 
, то (х + 1)2 
+0, а 
, или 
.
Аналогично показывается, что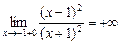 
.
Делаем вывод, что прямая х = –1 — вертикальная асимптота
графика.
Для нахождения наклонных асимптот у = k · x + b при 
находим пределы:
k = 
= 
= 
=
= 
= 
= 
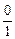= 0,
b = 
= 
= 
=
= 
= 
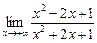= 1.
Таким образом, у = 1 — горизонтальная асимптота графика.
Аналогичным образом показывается, что у = 1 — горизонтальная асимптота и при х 
.
5. 
= 
=
= 
= 
= 
.
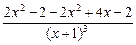6. Находим критические точки. Решаем уравнение y' = 0:
= 0 
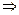
x = 1.
Точка х = –1, в которой производная не существует, не принадлежит D (y). Точка х = 1 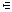D (y). Поэтому х = 1 — единственная критическая точка.
7. Критическая точка х = 1 разбивает область определения на интервалы. Определим знак первой производной у' на каждом интервале (рис. 14).
Рис. 14
.
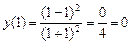Составим следующую таблицу:
| х | (–  ; –1)
| –1 | (–1; 1) | (1; )
| |
| y' | + | Не существует | – | + | |
| у | Возрастает | Не существует | Убывает | Возрастает | |
| Экстремума нет | min |
8. 
= 
=
= 
= 
=
= 
= 
.
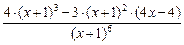9. Решим уравнение 
: = 0.
Отсюда 
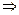
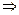х = 2.
Точка х = –1, в которой вторая производная не существует, не принадлежит D (y). Точка х = 2 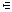D (y). Определим знак второй производной на области определения (рис. 15).
Рис. 15
.
Составим следующую таблицу:
| х | (– ; –1)
| –1 | (–1; 2) | (2; )
| |
| y'' | + | Не существует | + | – | |
| у | 
| Не существует |
| 1/9 | 
|
| График вогнутый | Перегиба нет | График вогнутый | Точка перегиба | График выпуклый |
10. Находим точки пересечения графика с осями координат.
10.1. С осью Ох. Так как у = 0, то имеем
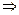
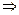
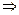х = 1.
10.2. С осью Оу. Так как х = 0, то имеем у =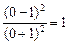 
.
Значит, (1,0), (0,1) — точки пересечения с осями координат.
Так как числитель и знаменатель дроби являются полными квадратами, то 
при всех х 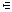D (y).
11. По результатам исследования строим график функции (рис. 16).
|
| Рис. 16 |
