При рассмотрении алгебраических критериев используются лишь коэффициенты характеристического уравнения и необходимые и достаточные условия устойчивости систем.
Необходимое условие является справедливым для всех систем:
Все коэффициенты характеристического уравнения должны быть положительными
Необходимое условие является и достаточным для систем 1-го и 2-го порядка.
Для устойчивости линейной САУ по критерию Гурвица необходимо и достаточно, чтобы были положительными n главных определителей матрицы коэффициентов характеристического уравнения заданной системы (знаменатель передаточной функции):
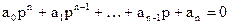
Матрица коэффициентов
По диагонали от левого верхнего угла до правого нижнего выписывают все коэффициенты по порядку от а1 до аn. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с чётными и нечётными индексами. В случае отсутствия даннного коэффициента или если его индекс <0 или >n, то на его место пишется 0.
а1 а3 а5 ………0 1=а1>0
а0 а2 а4 ………0 а1 а3
0 
а1 а3 а5…....0 2= а0 а2
………………. а1 а3 а5
……………..аn 3= а0 а2 а4
0 а1 а3
…………………
n =аn* n-1
Если аn=0, то имеет место апериодическая граница устойчивости.
Если n1=0, то это колебательная граница устойчивости.
Критерий Раусса.
Так же базируется на коэффициентах характеристического уравнения, из которого строится таблица.
Для устойчивости систем по критерию Раусса необходимо и достаточно чтобы при а0>0 все коэффициенты первого столбца таблицы Раусса были положительными.
| а0 | а2 | а4 | а6 | а8 |
| а1 | а3 | а5 | а7 | а9 |
| b1 | b2 | b3 | b4 | |
| c1 | c2 | c3 | … | … |
| … | … | … | … | … |
b1=(a1*a2-a0*a3)/a1
b2=(a1*a4-a0*a5)/a1
b3=(a1*a6-a0*a7)/a1
b4=(a1*a8-a0*a9)/a1
c1=(b1*a3-a1*b2)/b1
c2=(b1*a5-a1*b3)/b1……
Для устойчивости системы все коэффициенты 1-го столбца должны быть больше 0
а0>0, a1>0…
Частотные критерии
Критерий Михайлова.
Критерий базируется на поведении кривой, которую описывает конец вектора (X(ω),Y(ω)) замкнутой системы при изменении частоты от 0 до +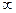 
.
Возьмём характеристический полином следующего вида:
(1)
Подставим в него 
и выделим вещественную и мнимую части.
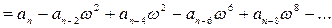
- вещественная часть,
- мнимая часть.
Изобразим годограф Михайлова выражения 
на комплексной плоскости.
Берём значения 
и строим годограф. Для различных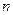 
годограф имеет формы, представленные на рисунке. Эти годографы называются кривыми Михайлова. Кривая Михайлова строится по точкам, рассчитывается 
и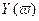 
для данной частоты, на кривой указываются значения частоты.
Формулировка критерия Михайлова.
Чтобы САР была устойчивой, необходимо и достаточно, чтобы вектор D (jω) при изменении частоты от 0 до +∞ начал движение с точки, лежащей на положительной вещественной оси, и, вращаясь только против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов комплексной плоскости, повернувшись на угол n∙π/2, где n – степень характеристического уравнения D (jω)= 0
Другими словами, требуется, чтобы кривая Михайлова проходила последовательно 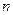квадрантов против часовой стрелки, всё время огибая начало координат и уходила в 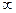в том квадранте, номер которого соответствует показателю степени полинома. Если это условие не выполняется, то система является неустойчивой.
Устойчивая Неустойчивая Апериодическая Колебательная
граница устойчивости граница устойчивости
Другая формулировка критерия Михайлова:
Она состоит в использовании свойства перемежаемости корней многочленов 
и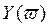 
.
Идя по кривой Михайлова от т. 
в направлении возрастания частоты, мы выходим из оси 
, затем пересекаем ось 
, потом снова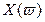 
и т. д.
Это значит, что корни уравнений 
и 
должны следовать поочерёдно друг за другом.
Кривые 
и 
имеют приблизительно такой вид:
Перемежаться должны корни 
, 
, 
,… Между ними должно быть следующее соотношение: 
Условием устойчивости системы является перемежаемость корней полиномов вещественной и мнимой частей комплексной передаточной функции. Нарушение этого условия говорит о неустойчивости системы.
