Типовые звенья
Это простые модели элементов сложных линейных систем и даже систем вцелом.
Переходная характеристика звеньев
Переходная характеристика или функция позволяет и качественно, и количественно характеризовать быстродействие звеньев и систем. Переходный процесс может быть как монотонным, так и колебательным и его длительность и является количественной характеристикой быстроты реакции звена на прикладываемые к нему воздействия.
Типовые звенья бывают:
- простейшие (пропорциональное звено, интегратор и дифференцирующее звено);
- звенья первого порядка (апериодическое или инерционное, инерционно-дифференцирующее, форсирующее и др.);
- звено второго порядка (колебательное и его частный случай – апериодическое второго порядка);
- звено третьего порядка (способное терять устойчивость, его можно назвать звеном Вышнеградского);
- звено запаздывания.
Основные характеристики линейных звеньев:
- переходная характеристика h (t) - реакция звена на ступенчатое единичное воздействие 1(t);
- передаточная функция W (s), связывающая изображения входного X (s) и выходного Y (s) сигналов линейного звена;
- комплексный коэффициент передачи W (j w), связывающий спектры входного X (j w) и выходного Y (j w) сигналов линейного звена;
- импульсная или весовая функция w (t) реакция звена на дельта-функцию Дирака d(t).
Типовые звенья линейных систем можно определять различными эквивалентными способами, в частности с помощью, так называемой передаточной функции, имеющей, как правило, дробно-рациональный вид, т.е. представляющей собой отношение двух полиномов:
где bi и aj – коэффициенты полиномов. Это т.н. параметры передаточной функции или звена.
Передаточная функция – это отношение изображения Y(p) выходного сигнала y(t) звена к изображению X(p) его входного сигнала x(t).
Т.е., передаточная функция позволяет по любому известному входному сигналу x(t) найти выходной y(t). Это значит, что с точки зрения ТАУ передаточная функция полностью характеризует систему управления или ее звено. Это же самое можно сказать и в отношении совокупности коэффициентов полиномов числителя и знаменателя передаточной функции.
Наличие нулевых корней в числителе или знаменателе передаточной функции типовых звеньев - это признак для разбиения последних на три группы:
- Позиционные звенья: 1, 2, 3, 4, 5, - не имеют нулевых корней, и, следовательно, в области низких частот (т.е. в установившемся режиме), имеют коэффициент передачи равный k.
- Интегрирующие звенья: 6, 7, 8, - имеют нулевой корень-полюс, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к бесконечности.
- Дифференцирующие звенья: 9, 10 - имеют нулевой корень-ноль, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к нулю.
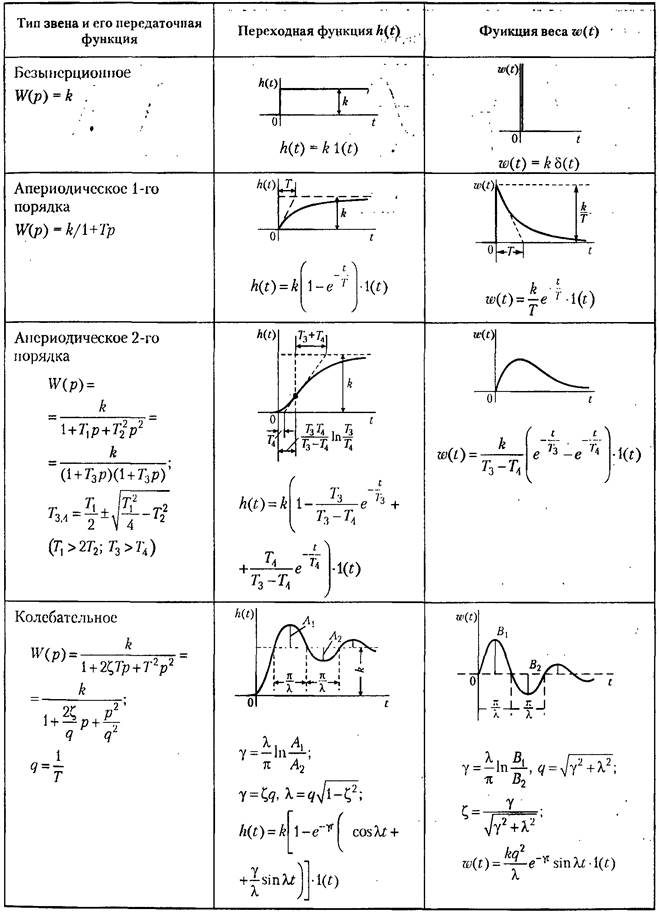
Переходные и весовые характеристики основных типовых звеньев приведены в Таблице 1. Перечисленные линейные звенья содержат один вход и один выход. Существует еще одно линейное звено, которое может иметь несколько, больше одного, входов и один выход: сумматор. Сумматор - необходимое звено для построения модели достаточно сложной системы, состоящей из нескольких звеньев.
Типовых звеньев всего около полутора десятков, но из них, как из кубиков (или, если угодно, как любое сложное вещество из отдельных химических элементов), можно построить модель линейной системы управления любой сложности.
Минимальный набор звеньев, который позволяет построить модель линейной системы любой сложности, в том числе и самих типовых звеньев, состоит всего из трех звеньев: пропорционального, интегратора и сумматора. Однако модель, построенную из этих трех звеньев, бывает труднее анализировать, чаще удобнее применять кроме них еще несколько типов звеньев.
Таблица 1. Передаточные, переходные и весовые функции типовых звеньев.
Позиционные
Интегрирующие
Дифферецирующие
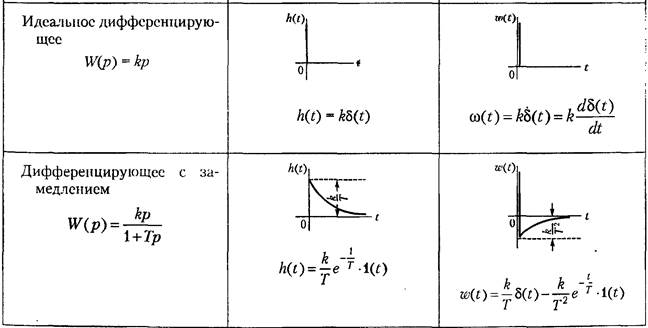
Соединение звеньев.
4. Частотные характеристики
Частотная передаточная функция получается из обычной заменой оператора Лапласа s(или р) на комплексную частоту j w, т.е. в результате перехода от изображения Лапласа к изображению Фурье.
Дифференциальное уравнение движения системы связывает входной и выходной сигналы (т.е. функции времени), передаточная функция связывает изображения Лапласа тех же сигналов, а частотная ПФ связывает их спектры.
Частотная передаточная функция может быть представлена в следующих видах:
W (j w) = A (w) e j j(w), или W (j w) = U (w) + jV (w);
где:
· A (w) - модуль частотной передаточной функции - находится как отношение модулей числителя и знаменателя:
· j(w) - фаза частотной передаточной функции - находится как разность аргументов числителя и знаменателя:
· 
U (w) и V (w) - вещественная и мнимая части частотной ПФ. Для их нахождения необходимо избавиться от мнимости в знаменателе, умножением на сопряженную знаменателю комплексную величину.
