Розглянемо систему (1.1) у двовимірному випадку. Через кожну точку 
фазової площини проходить єдина фазова крива, за виключенням особливих точок 
, таких що
Лінеаризуємо систему в околі точки рівноваги . Процедура лінеаризації (1.1): 
. В новій системі координат 
положенню рівноваги відповідає точка (0,0). Якщо f і g – аналітичні функції поблизу , то можна розкласти f і g в ряд Тейлора в околі цієї точки. Зважаючи на те, що в точці рівноваги 
, та знехтувавши величинами більш за першого за перший порядок малості, отримаємо лінеаризовану в околі систему відносно змінних :
Введемо позначення:
.
Розв'язки лінійної системи
(1.5)
дають параметричні (t – параметр) форми фазових кривих поблизу нерухомої точки .
Нехай 
та 
– власні значення матриці А, тобто
. (1.6)
Отже, розв’язки (1.5) мають вигляд:
(1.7)
де 
– довільні константи, а 
– власні вектори матриці А, які відповідають 
і визначаються за формулою:
(1.8)
Виключення параметра t в (1.7) дає фазові криві на площині (x,y) поблизу точки рівноваги . Вираз (1.7) використовується, якщо власні значення не є рівними. Якщо ж 
, то розв’язки (1.5) будуть пропорційні 
.
Далі розглянемо вплив власних значень матриці А на характер особливої точки лінійної системи (1.5). Для спрощення викладення вважатимемо, що точкою рівноваги є (0,0).
I)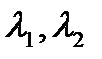 
є дійсними числами і не дорівнюють один одному.
а) і мають однаковий знак. Типові власні вектори 
зображені на рис. 1. 3,а. Нехай 
Тоді, згідно з (1.7), наприклад, при 
справедливий вираз 
. Значить, точка на фазовій площині рухається лише уздовж 
у напрямку початку координат при 
: якщо 
– уздовж PО; якщо 
– уздовж QO. Згідно з (1.7), кожний розв’язок наближається до (0,0) при , тому що при 
коли 
. Отже 
~ 
при .
Таким чином, поблизу початку координат всі розв’язки наближаються до нуля уздовж 
, як зображено на рис. 1.3,а. Така особлива точка називається вузол (тип I). Якщо 
, це буде стійкий вузол, оскільки всі траєкторії наближуються до (0,0) при . Якщо 
, це – нестійкий вузол; оскільки 
при (рис. 1.3,б).
Рис.1.3. Особлива точка – вузол: а – стійкий, б – нестійкий
б) і мають різні знаки. Припустимо, наприклад, що 
. Тоді, 
уздовж 
при , в той час як 
уздовж 
при 
.
Таким чином, рух уздовж 
і 
відбувається в різних напрямках; розв’язки поблизу (0,0) зображені на рис. 1.4,а. Така точка рівноваги називається сідловою точкою. Вона завжди нестійка, за виключенням руху строго вздовж напрямку вектора.
II) і є комплексними числами: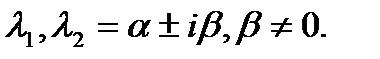 
Розв’язок (1.7) в цьому випадку включає в себе 
і, отже, коливально наближується до точки (0,0) або віддаляється від неї.
а) 
. В цьому випадку виникає точка рівноваги фокус, який є стійким при 
і нестійким при 
. На рис. 1.4,б зображена особлива точка на кшталт фокуса.
б) 
. В цьому випадку фазові криві представляють собою еліпси. Така особлива точка – центр; її зображено на рис 1.4, в.
У випадку особливих точок такого типу, знайдених за допомогою лінійного наближення функцій 
і 
, необхідно розглядати члени більш високого порядку (ніж лінійні) для того, щоб визначити, стійкі вони чи ні.
Рис.1.4. Особлива точка: а – сідло, б – фокус, в – центр
ІІІ) 
.
а) Розв'язки включають члени типу 
і в даному випадку існує тільки єдиний власний вектор 
, уздовж якого розв'язки прямують до (0,0). Параметр 
у виразі впливає на поведінку розв'язку далеко від (0,0). Ця точка називається вузол (тип ІІ); вона зображена на рис. 1.5,а.
б) Якщо розв'язки не включають члена , то особлива точка називається діакритичною, і може бути як стійкою, так і нестійкою залежно від знака 
. Траєкторії поблизу діакритичної особливої точки наведено на рис. 1.5,б.
Рис.1.5. Особлива точка: а – вузол (тип ІІ), б – діакритична
Таким чином, тип особливою точки залежить від параметрів 
в матриці А в (1.5). На рис. 1.6 підведений підсумок викладеним вище результатам в термінах сліду і визначника матриці А.
Рис. 1.6. Підсумкова діаграма, яка демонструє вплив сліду 
= 
і визначника 
на характер особливої точки
