Способ концентрических сфер- посредников

Способ концентрических сфер- посредников для построения линии пересечения поверхностей можно использовать при наличии следующих условий:

1. Обе поверхности должны быть поверхностями вращения.

2. Оси поверхностей должны пересекаться между собой.

3. Оси поверхностей должны быть параллельны одной из плоскостей проекций.

Если последнее условие не выполняется, то путем преобразования чертежа систему приводят в такое положение, при котором плоскость осей становится параллельной какой- либо плоскости проекций.

В основе метода концентрических сфер- посредников лежит следующая теорема: две соосные поверхности вращения пересекаются по окружностям, число которых равно числу точек пересечения меридианов поверхностей. Если общая ось этих поверхностей параллельна какой- либо плоскости проекций, то на эту плоскость проекций окружности проецируются прямолинейными отрезками.

Предположим, что некоторая поверхность вращения Ф (i,m) пересекается со сферой Ф’ (i,n), причем центр сферы находится на оси этой поверхности, то есть сфера будет соосна с поверхностью Ф и в пересечении получатся окружности, которые образуются при вращении точек пересечения меридианов m и n (рис. 10.2).

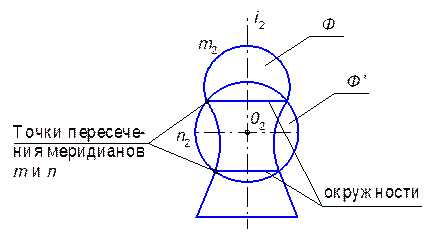Рис.12.2

План решения задачи способом концентрических сфер- посредников можно сформулировать так:

1. Принимая точку пересечения осей заданных поверхностей за центр, строят вспомогательные сферы- посредники.

2. Сфера- посредник будет соосна каждой из заданных поверхностей, а поэтому пересечет их по окружностям, которые строятся на основании точек пересечения меридианов.

3. Находят общие точки пересечения полученных окружностей. Эти точки и принадлежат искомой линии пересечения поверхностей.

Пример. Построить линию пересечения конуса вращения Ф(i,l) c цилиндром вращения Ф’(i’,l’), оси которых параллельны фронтальной плоскости проекций и пересекаются в точке 0 (рис. 10.5).

Решение. Из точки 0 ₂ как из центра описывают окружность, которая является фронтальной проекцией сферы- посредника (рис. 12.3). Эта сфера соосна как с цилиндром, так и с конусом, и поэтому рассекает их по окружностям, которые на фронтальной плоскости проекций изобразятся отрезками прямых: на цилиндре S ₂ P ₂ (окружность а) и Н ₂ L ₂ (окружность в); на конусе M ₂ N ₂ (окружность m) и K ₂ T ₂ (окружность n).

Рис. 12.3

На пересечении этих отрезков (окружностей) получают точки 1₂,2₂,3₂,4₂, принадлежащие обеим данным поверхностям и, следовательно, искомой линии пересечения. На фронтальной проекции точки 1₂,3₂- видимые, а точки 2₂,4₂- невидимые, так как расположены на невидимой половине поверхности.

Для построения горизонтальной проекции точек удобно пользоваться окружностями (в нашем случае окружностью n), полученными на сферах- посредниках, плоскости которых параллельны горизонтальной плоскости проекций. На рис. 12.3 показано построение точек 1₁, 2₁, 3₁, 4₁.

Изменяя радиус вспомогательной сферы, можно получить достаточное количество точек для построения искомой линии пересечения. Однако начинать решение задачи нужно с определения радиуса максимальной и минимальной секущих сфер (рис. 12.4).

Для определения радиуса максимальной сферы отмечают точки пересечения очерковых образующих цилиндра и конуса, лежащих в общей плоскости симметрии обеих фигур (на - это точки A ₂, B ₂, C ₂, D ₂). Радиус Rmax

равен расстоянию от точки 0 ₂ до самой удаленной точки пересечения очерковых образующих, в нашем случае до точки B ₂. Итак, Rmax = 0 ₂ B ₂ (рис. 12.4).

Радиус Rmin наименьшей сферы- посредника должен быть равен радиусу сферы касательной к одной поверхности и пересекающей другую (в нашем случае-касательной к конусу и пересекающей цилиндр).

Необходимо определить точки E ₁, F ₁, M ₁, N ₁ (рис. 12.5), лежащие на горизонтальном очерке цилиндра, так как на горизонтальной проекции они являются точками видимости и отделяют видимую часть кривой от невидимой.

Рис. 12.4