Способы преобразования комплексного чертежа позволяют преобразовывать прямые и плоскости общего положения в частное положение относительно плоскостей проекций, что облегчает решение позиционных и метрических задач.
Способы замены плоскостей проекций
Этот способ заключается в замене одной из заданных плоскостей проекций новой, перпендикулярной к оставляемой плоскости проекций. При этом сохраняется принцип ортогональности: линии связи в новой системе плоскостей перпендикулярны новой оси.
Если замена одной плоскости проекций недостаточна, то прибегают к последовательной замене обеих плоскостей проекций.
Замена одной плоскости проекций
Пусть дана точка А проекциями А 1 и А 2 на плоскостях 
и 
. Введем новую плоскость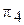 
, перпендикулярную горизонтальной плоскости проекций и на ней получим новую проекцию точки А 4 (рис. 8.1). Очевидно, что расстояние новой проекции А 4 от новой оси х 14 равно расстоянию фронтальной проекции А 2 от оси х 12.
На эпюре после совмещения плоскости 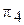с плоскостью новая проекция А 4 располагается на линии связи, перпендикулярной новой оси х 14, причем расстояние от новой оси х 14 до новой проекции А 4 равно расстоянию от заменяемой оси х 12 до заменяемой проекции А 2.
Пример: Определить истинную величину отрезка АВ способом замены плоскостей проекций (рис. 8.2)
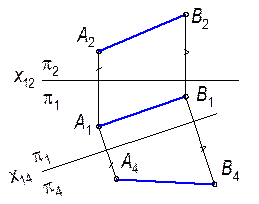
Рис. 8.2
Заменим плоскость на плоскость 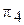, перпендикулярную и параллельную заданному отрезку АВ. При этом новая ось х 14 займет положение, параллельное горизонтальной проекции АВ. Символическая запись преобразования: 
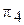; // AB (на эпюре х 14// A 1 B 1).
Через концы отрезка A 1 B 1 проведем линию связи, перпендикулярную новой оси и отложим на них отрезки, равные расстоянию точек A 2 и В 2 от оси х 12. Полученная проекция A 4 B 4 является натуральной величиной отрезка AB.
Замена двух плоскостей проекций
В том случае, когда одной заменой плоскостей проекций не удается достичь желаемого частного положения геометрического объекта относительно плоскостей проекций, производят две последовательные замены плоскостей проекций.
Например, преобразование отрезка прямой общего положения в проецирующую прямую возможно в результате двух следующих преобразований (рис. 8.3).
1) ; 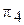// AB (на эпюре х 14// A 1 B 1).
2) 
; 
// AB (на эпюре х 45// A 4 B 4).
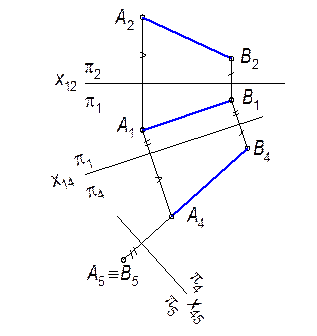
Рис. 8.3
Задачи
5.1.3.1. Найти горизонтальную проекцию отрезка AB, длина которого 45 мм.
8.1.3.2. Найти фронтальную проекцию точки К 1, отстоящей от горизонтали h на 20 мм.
8.1.3.3. Определить расстояние от точки М до плоскости 
(АВС).
8.1.3.4. Определить углы наклона прямой АВ к плоскостям проекций и .
8.1.3.5. Определить расстояние между параллельными плоскостями 
и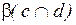 
.
8.1.3.6. Определить углы наклона плоскости (АВС) к плоскостям проекций и .
8.1.3.7. Определить расстояние между параллельными прямыми a и b.
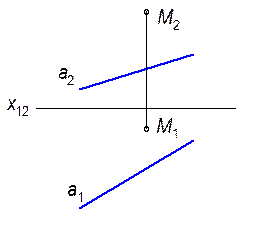
8.1.3.8. Определить расстояние от точки М до прямой а.
8.1.3.9. Построить проекции прямоугольного равнобедренного 
АВС, катет АВ которого принадлежит прямой а. Угол при вершине А – прямой.
8.1.3.10. Найти горизонтальную проекцию точки D, равноудаленной от вершин заданного треугольника АВС.
8.1.3.11. Найти горизонтальную проекцию прямой СD, параллельной прямой АВ, если известно, что расстояние между ними равно 20мм. Указать количество решений.
8.1.3.12. Провести прямую m, параллельной двум заданным прямым а и b и удаленную от прямой a на 20мм и от прямой b на 15мм. Указать количество решений.
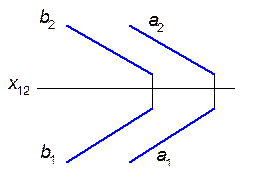
8.1.3.13. Построить проекции квадрата ABCD по данной его стороне АВ и направлению а 2 фронтальной проекции смежной с АВ стороны АD.
Способ вращения
Способ вращения заключается в том, что геометрический объект вращают вокруг некоторой оси до требуемого положения относительно плоскостей проекций. При этом все точки объекта описывают дуги окружностей в плоскостях, перпендикулярных оси вращения. Центры этих дуг располагаются на оси вращения, а радиусы равны кратчайшему расстоянию от вращаемых точек до оси. Оси вращения располагают параллельно или перпендикулярно одной из плоскостей проекций.
