
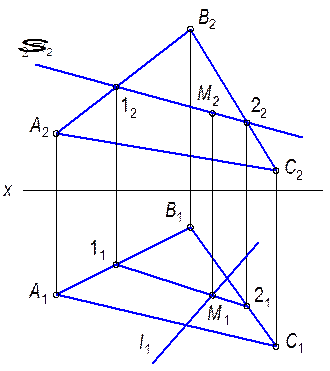
Рис. 5.1 Рис. 5.2
Пересечение прямой с плоскостью Параллельность прямой и плоскости
1. Точка пересечения прямой с плоскостью (точка встречи) определяется как точка, принадлежащая одновременно и прямой и плоскостью.
2. Если плоскость частного положения, то траектория точки пересечения с прямой находится на пересечении следа-проекции плоскости с соответствующей проекцией прямой, а вторая из условия принадлежности с прямой.
3. Если плоскость и прямая общего положения, то точка встречи находится в такой последовательности:
а) прямую заключаем в проецирующую плоскость;
б) строим линию пересечения вспомогательной (проецирующей) и заданной плоскостей;
в) находим точку встречи на пересечении полученной линии с заданной прямой.
4. Признаком параллельности прямой и плоскости частного положения является параллельность следа-проекции плоскости соответствующей проекции прямой.
5. Признаком параллельности плоскости и прямой является параллельность прямой некоторой прямой плоскости.
Задачи
5.1.1. Построить точку пересечения прямой АВ с плоскостью (q ^ p2).
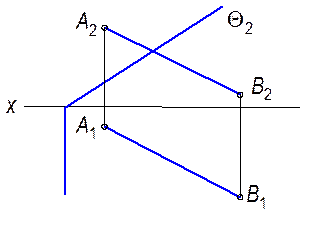
5.1.2. Построить точку пересечения прямой СD и плоскостью Г(Г ^ p1).

5.1.3. Построить проекции точки пересечения прямой m c плоскостью  (АВС).
(АВС).

5.1.4. Построить точку пересечения прямой m с плоскостью S(f Ç h).

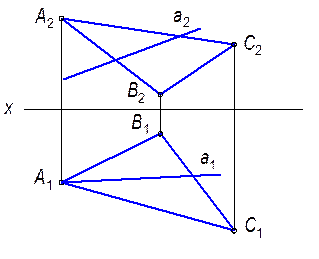
5.1.5. Построить точку пересечения прямой l с плоскостью a (а Ç b).

5.1.6. Построить точку пересечения прямой а с плоскостью  (АВС).
(АВС).
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Рис. 6.1 Рис. 6.2
В основе перпендикулярности прямых и плоскостей на чертеже положена теорема о прямом угле: Если одна из сторон прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то на эту плоскость прямой угол проецируется без искажения.
1. Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым плоскости. Такими прямыми на эпюре выбираются пересекающиеся линии уровня плоскости (горизонталь, фронталь, профильная прямая). Тогда проекции перпендикуляра будут перпендикулярны соответствующим проекциям линий уровня плоскости (Г1^ h 1; Г2^ f 2; Г3^ p 3).
2. Две плоскости взаимно перпендикулярны, если в одной из них возможно провести прямую, перпендикулярную к другой плоскости.
3. Две прямые взаимно перпендикулярны, если одна из них лежит в плоскости, перпендикулярной второй прямой (если через одну из них можно провести плоскость, перпендикулярную второй прямой).
Задачи
6.1.1. Построить проекции равнобедренного ∆ АВС, если СМ (СМ êêp1) высота А Î p1; В Î p2.

6.1.2. Построить проекции ромба АВСD, если АС (АС êêp2) диагональ ромба, В Î p1; D – равноудалена от плоскостей p1 и p2.

6.1.3. Построить проекции ∆ АВС с прямым углом при вершине А, гипотенуза ВС которого лежит на прямой l.

6.1.4. Через точку А провести проекции прямой, перпендикулярной к плоскости å (f Ç h).

6.1.5. Через точку А провести проекции прямой, перпендикулярной к плоскости ∆ (АВС).

6.1.6. Через точку К провести проекции перпендикуляра к плоскости å (а Ç b).

6.1.7. Через точку А провести проекции плоскости, перпендикулярной к прямой ВС.

6.1.8. В точке М пересечения медиан (центр тяжести) ∆ АВС провести перпендикуляр к его плоскости.

МНОГОГРАННИКИ
Если все точки линии принадлежат поверхности, то линия принадлежит поверхности.
Если точка принадлежит линии, а линия поверхности, то точка принадлежит поверхности.
Задачи
7.1.1. Построить недостающие проекции точек, принадлежащих поверхностям геометрических фигур.

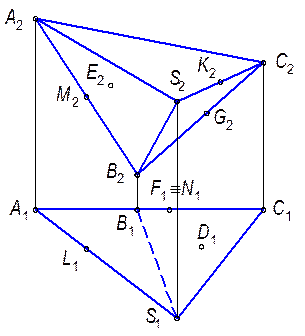
7.1.2. Построить недостающие проекции линий, принадлежащих поверхностям геометрических фигур.


7.1.3. Построить линию пересечения пирамиды с плоскостью.


7.1.4. Построить линию пересечения плоскости с геометрическими фигурами.


7.1.5. Построить точки пересечения прямой с геометрическими фигурами.
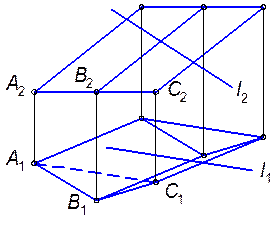

7.1.6. Построить линию пересечения двух многогранников и определить видимость.








