Этот способ применяется для определения натуральной величины плоских фигур и углов. Геометрический объект вращается вокруг линии уровня до положения, параллельного одной из плоскостей проекций.
Например, вращением вокруг горизонтали плоскость общего положения, заданную 
АВС, преобразуем в горизонтальную плоскость уровня (рис. 108). В качестве оси вращения выберем сторону АВ, являющуюся горизонталью и повернем АВС до совмещения с горизонтальной плоскостью, проходящей через сторону АВ (горизонталь).
Так как, вершины А и В принадлежат оси вращения, они при вращении неподвижны. Рассмотрим вращение точки С.
1. Через точку С проведем плоскость ее вращения – горизонтально- проецирующую плоскость w, перпендикулярную горизонтали (оси вращения).
2. Отметим центр вращения 0 точки А, как точку пересечения плоскости w и горизонтали.
3. Определим радиус вращения точки С: проекции 0 1 С 1, 0 2 С 2 и натуральную величину радиуса 0 1 С 0 (определяется методом прямоугольного треугольника).
4. Находим новую проекцию вершины С (точку 
), которая расположится в плоскости вращения w на расстоянии 0 1 С 0 от горизонтали (так как плоскость АВС вращается до положения горизонтальной плоскости, все прямые в ней изображаются в натуральную величину, в том числе и отрезок 0С).
5. Соединив точки А 1, В 1 с точкой 
найдем натуральную величину АВС.
Вращение вокруг проецирующей прямой
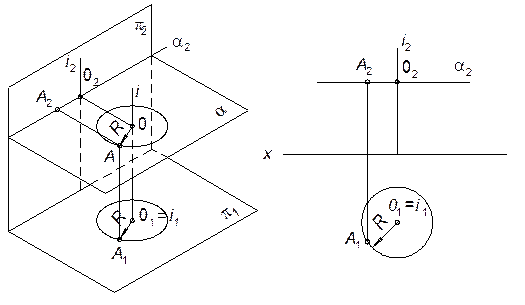
Рис. 8.2.2.1
Пусть точка А вращается вокруг оси i, перпендикулярной горизонтальной плоскости проекции (рис. 91). Вращаясь, точка А будет описывать окружность в плоскости, перпендикулярной оси вращения и, следовательно, параллельной горизонтальной плоскости проекций 
. Поэтому на плоскость эта окружность спроецируется без искажений, а на плоскость 
- в виде отрезка, параллельного плоскости .
Таким образом, при вращении точки вокруг проецирующей прямой на плоскости перпендикулярной оси вращения, проекция точки перемещается по дуге окружности, а на плоскости, параллельной оси вращения - по прямой линии, параллельной оси ox.
Вращение прямой линии и плоскости сводится к вращению на один и тот же угол двух точек, принадлежащих прямой, а вращение плоскости – трех ее точек, не лежащих на одной прямой.
Пример 1: Повернем прямую общего положения АВ до положения горизонтали.
Выберем ось вращения i, проходящую через точку А и перпендикулярную плоскости . В этом случае достаточно повернуть точку В, так как точка А является неподвижной. Фронтальная проекция точки В вращается по дуге окружности радиуса А 2 В 2 до положения, параллельного оси ox, горизонтальная проекция перемещается по линии, параллельной оси ox. Новая горизонтальная проекция 
отражает натуральную величину отрезка АВ, а угол между и осью ox – угол наклона АВ к плоскости .
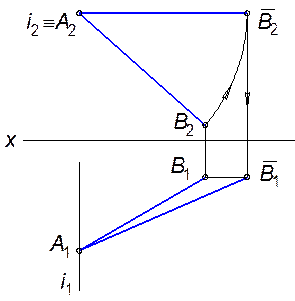
Рис. 8.2.2.2
Пример 2: Повернем плоскость общего положения 
(АВС) до положения, перпендикулярного плоскости .
Горизонталь фронтально-проецирующей плоскости является фронтально-проецирующей прямой. Поэтому в плоскости проведем горизонталь h и повернем ее вокруг горизонтально-проецирующей оси i до положения, перпендикулярного плоскости .
Ось вращения проведем через вершину А, следовательно она при вращении остается неподвижной и достаточно повернуть две другие вершины АВС на одинаковый угол. Учитывая, что при вращении горизонтальная проекция не изменяется по виду и величине, находим новую проекцию вершины В на дуге радиуса А 1 В 1 на расстоянии 11 В 1 от нового положения точки 
. Точка лежит на пересечении дуги радиуса А 1 С 1 и продолжения прямой 
. Фронтальные проекции точек В и С перемещаются по линиям параллельным оси ox, до пересечения с соответствующими линиями связи от точек 
и . Новая фронтальная проекция АВС (
) позволяет определить угол наклона плоскости к плоскости 
.
Рис. 8.2.2.3
