Задача 5. По многолетним данным для данного района вероятность весенних засух равна 0,4, а летних – 0,6. Какова вероятность того, что в наступающем году будет засуха.
Решение. Испытание – предположение урожайности на следующий год. Событие А – в наступающем году будет засуха. Событие В – предполагается весенняя засуха. Событие С – предполагается летняя засуха. Год будет засушливым, если произойдет или весенняя, или летняя, или весенняя и летняя засухи совместно. Следовательно, события В и С совместные. Искомая вероятность
 .
.
Полагая, что весенняя и летняя засухи – события независимые, получим
 .
.
Значит,
 .
.
Ответ. Вероятность того, что в данном районе наступающий год будет засушливым равна 0,76, или 76%.
Задача 6. Три стрелка производят по одному выстрелу в цель независимо друг от друга. Вероятности попадания в цель для каждого из них равны соответственно 0,7; 0,8; 0,9. Найти вероятность того, что: а) в цель попадет только один стрелок; б) в цель попадут только два стрелка; в) в цель попадет хотя бы один стрелок.
Решение. а) Рассмотрим следующие события:
 – первый стрелок попал в цель;
– первый стрелок попал в цель; 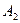 – второй стрелок попал в цель;
– второй стрелок попал в цель;  – третий стрелок попал в цель;
– третий стрелок попал в цель; 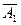 – первый стрелок не попал в цель;
– первый стрелок не попал в цель;  – второй стрелок не попал в цель;
– второй стрелок не попал в цель;  – третий стрелок не попал в цель.
– третий стрелок не попал в цель.
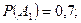


По условию


Пусть событие В – попал только один стрелок. Тогда
 .
.
Отсюда в силу несовместности событий-слагаемых и независимости событий-сомножителей
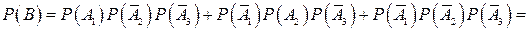
 .
.
б) Пусть событие С – попадут только два стрелка. Тогда
 .
.
Отсюда
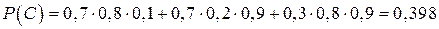 .
.
в) Пусть событие  – попал хотя бы один стрелок. Тогда противоположное событие
– попал хотя бы один стрелок. Тогда противоположное событие  – не попал ни один из них, т.е
– не попал ни один из них, т.е  Поэтому
Поэтому  Отсюда
Отсюда
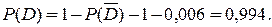
Ответ. 1) Вероятность попадания в цель только одного стрелка равна 9,2%. 2) Вероятность попадания в цель только двух стрелков равна 40%. 3) Вероятность попадания в цель хотя бы одного стрелка – 99,4%.
Задача 7. Среди 15 микрокалькуляторов, имеющихся в вычислительной лаборатории, лишь 6 новых, а остальные – бывшие в употреблении. Наугад взято три микрокалькулятора. Какова вероятность, что все они окажутся новыми?
Решение. Рассмотрим события: А – первый из взятых микрокалькуляторов новый; В – второй микрокалькулятор новый; С – третий микрокалькулятор новый. Тогда
 .
.
Вероятность того, что второй микрокалькулятор будет новый, при условии, что первым уже был отобран новый микрокалькулятор, т.е. условная вероятность события В, равна
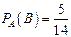 .
.
Вероятность того, что третьим будет отобран новый микрокалькулятор, при условии, что уже отобраны два новых микрокалькулятора, т.е. условная вероятность события С равна
 .
.
Искомая вероятность того, что все три отобранных микрокалькулятора окажутся новыми, равна:
 .
.
Ответ. Вероятность того, что все три отобранных калькулятора новые равна 4,4%.
Задача 8. Известно, что на факультете 80% студентов-заочников могут получить вызов на экзаменационную сессию. Найти вероятность того, что из 40 случайно отобранных студентов факультета 30 получат вызов.
Решение. Будем считать случайный отбор студентов проведением 40 независимых испытаний. Испытание – отбирается один студент. Событие А – отобранный студент получил вызов. Для каждого выбранного студента вероятность получить вызов на сессию постоянна и задана в процентах. Разделив на 100%, получим, что
 .
.
Вероятность противоположного события, состоящего в том, что студент не получит вызова на сессию, равна
 .
.
Найти надо вероятность сложного события 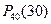 , состоящего в том, что в 40 испытаниях событие А появится ровно 30 раз. Так как
, состоящего в том, что в 40 испытаниях событие А появится ровно 30 раз. Так как 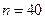 и
и  относительно велики, то выполнять трудоемкие вычисления по формуле Бернулли нерационально. Воспользуемся приближенной локальной формулой Лапласа.
относительно велики, то выполнять трудоемкие вычисления по формуле Бернулли нерационально. Воспользуемся приближенной локальной формулой Лапласа.
По условию задачи  . Вычислим:
. Вычислим:
1) 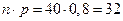 ;
;
2)  ;
;
3)  ;
;
4) находим по таблице значение функции вероятностей  . Так как это четная функция, т.е
. Так как это четная функция, т.е  .
.
Искомая вероятность равна
 .
.
Ответ. Вероятность того, что из 40 случайно отобранных студентов факультета только 30 будут иметь вызов на сессию, равна, 0,1154 или около 11,5%.
Задача 9. Вероятность поражения мишени при каждом выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах будет не менее 70 поражение мишени?
Решение. Будем считать произведение 100 выстрелов числом независимых повторных испытаний, в которых число k – число поражений мишени, может принимать значения от 70 до 100, т.е.
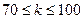 .
.
Испытание – сделан один выстрел. Событие А – мишень поражена. Вероятность появления события А в каждом испытании, т.е. вероятность поражения мишени, постоянна и равна  , вероятность промаха
, вероятность промаха  . Так как
. Так как  велико и рассматривается в заданном промежутке (70; 100), то расчеты вероятности проведем по интегральной формуле Лапласа. По условию задачи:
велико и рассматривается в заданном промежутке (70; 100), то расчеты вероятности проведем по интегральной формуле Лапласа. По условию задачи:
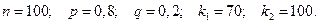
Вычислим:
1)  ;
;
2) 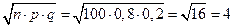 ;
;
3) 
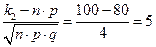 ;
;
4) 
 ;
;
5) искомую вероятность найдем по формуле
 .
.
По таблице значений функции Лапласа Ф(х) находим, что  , так как функция нечетная, т.е.
, так как функция нечетная, т.е.  . Значение функции Ф(х) при
. Значение функции Ф(х) при 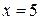 можно в таблице не искать, так как
можно в таблице не искать, так как 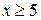 значение Ф(х) постоянно и равно 0,5. Тогда
значение Ф(х) постоянно и равно 0,5. Тогда
 .
.
Ответ. Вероятность поражения мишени в серии из 100 выстрелов от 70 до 100 раз близка к 100% – практически достоверное событие.
Задача 10. Сколько нужно посеять семян, всхожесть которых 70%, чтобы наивероятнейшее число взошедших семян было равно 60?
Решение. По условию задачи  – вероятность того, что посаженное семя взойдет;
– вероятность того, что посаженное семя взойдет; 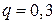 – вероятность того, что семя не даст всхода;
– вероятность того, что семя не даст всхода;  – наивероятнейшее число взошедших семян. Число посеянных семян n требуется найти. Наивероятнейшее число
– наивероятнейшее число взошедших семян. Число посеянных семян n требуется найти. Наивероятнейшее число  взошедших семян найдем по формуле
взошедших семян найдем по формуле
 .
.
Подставив данные величины в эту формулу, получим

и переходим к системе неравенств:
 .
.
Поскольку число семян  является целым числом, то
является целым числом, то  или
или 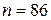 .
.
Ответ. Чтобы при заданной вероятности взошло 60 семян, необходимо посадить 85–86 семян.
Задача 11. Установлено, что всхожесть партии гороха составляет 95%. Отбирается 6 зерен. Какова вероятность того, что они дадут не менее 5 всходов? не более 3 всходов?
Решение. Будем считать высев 6 зерен гороха проведением 6 независимых испытаний. Для каждого из 6 посаженных зерен вероятность прорасти постоянна и задана в процентах. Испытание – посадили одно зернышко гороха. Событие А – посаженное зерно взойдет. Событие В – посаженные 6 зерен гороха дадут не менее 5 всходов. Событие С – посаженные 6 зерен гороха дадут не более 3 всходов. По условию задачи вероятность того, что посаженное зерно гороха взойдет, в каждом отдельном испытании одинакова и равна  . Тогда вероятность противоположного события, что посаженное зерно не даст всхода, равна
. Тогда вероятность противоположного события, что посаженное зерно не даст всхода, равна
 .
.
Вероятность сложного события В, состоящего в том, что дадут всходы 5 или 6 зерен, будем вычислять по формуле Бернулли.
 .
.
Вероятность сложного события С, состоящего в том, что из 6 зерен гороха дадут всходы или не одно, или 1, или 2, или 3, находим по формуле Бернулли.

Ответ. Вероятность того, что при посадке 6 зерен гороха дадут всходы не менее 5 зерен равна 0,967, а не более 3 зерен – 0,002.
Задача 12. Магазин продает продукцию трех сортов, причем первого сорта – 70%. На специализированном заводе изготовлено 25% продукции первого сорта, 75% продукции второго сорта и 25% продукции третьего сорта, продаваемой магазином. Сколько процентов продукции третьего сорта продает магазин, если взятая на контроль продукция оказалась изготовленной на специализированном заводе, а вероятность того что эта продукция 1-го сорта равна 50%.
Решение. Испытание – взята на контроль продукция, продаваемая в магазине.
Событие А – продаваемая магазином продукция, взятая на контроль, изготовлена на специализированном заводе. Событие В1 – продаваемая магазином продукция первого сорта. Событие В2 – продаваемая магазином продукция второго сорта. Событие В3 – продаваемая магазином продукция третьего сорта, причем события В1, В2, В3 составляют полную группу событий, поэтому 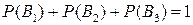 .
.
По условию задачи  , следовательно
, следовательно  . Событие А, состоящее в том, что продаваемая магазином продукция изготовлена на специализированном заводе, можно выразить так:
. Событие А, состоящее в том, что продаваемая магазином продукция изготовлена на специализированном заводе, можно выразить так:
 .
.
Следовательно, можно применить формулу Байеса
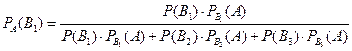 .
.
По условию задачи:
 ;
;  ;
; 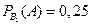 ;
;  ;
;  .
.
Кроме того  . Подставляя все это значения в формулу Байеса, получаем
. Подставляя все это значения в формулу Байеса, получаем
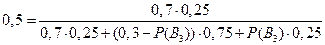 ,
,
 ,
,
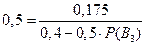 ,
,
 ,
,
 .
.
Ответ. Магазин продает 10% продукции третьего сорта.
Индивидуальные задания по теме «Случайные величины»
ЗАДАЧА 10 (№ 1–20)
Даны две независимые дискретные случайные величины X и Y, которые заданы своими законами распределения. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z = 3X-2Y.
| X | -6 | Y | -8 | ||||||
| P | 0,1 | 0,1 | 0,6 | 0,2 | P | 0,4 | 0,6 |
| X | -2 | -1 | Y | -3 | |||||
| P | 0,2 | 0,5 | 0,1 | 0,2 | P | 0,3 | 0,7 |
| X | -5 | -4 | -2 | Y | -8 | -1 | |||
| P | 0,1 | 0,5 | 0,2 | 0,2 | P | 0,7 | 0,3 |
| X | -6 | -3 | Y | -2 | |||||
| P | 0,3 | 0,3 | 0,2 | 0,2 | P | 0,2 | 0,8 |
| X | -4 | -2 | -1 | Y | -3 | -1 | |||
| P | 0,1 | 0,3 | 0,2 | 0,4 | P | 0,4 | 0,6 |
| X | -2 | Y | |||||||
| P | 0,5 | 0,1 | 0,2 | 0,2 | P | 0,2 | 0,8 |
| X | -7 | -5 | -2 | Y | -3 | ||||
| P | 0,4 | 0,4 | 0,1 | 0,1 | P | 0,1 | 0,9 |
| X | -1 | Y | -2 | ||||||
| P | 0,2 | 0,5 | 0,1 | 0,2 | P | 0,8 | 0,2 |
| X | -8 | -6 | -1 | Y | |||||
| P | 0,5 | 0,1 | 0,2 | 0,2 | P | 0,2 | 0,8 |
| X | -2 | Y | |||||||
| P | 0,1 | 0,1 | 0,3 | 0,5 | P | 0,1 | 0,9 |
| X | -7 | Y | -3 | ||||||
| P | 0,5 | 0,1 | 0,3 | 0,1 | P | 0,3 | 0,7 |
| X | -4 | -1 | Y | ||||||
| P | 0,1 | 0,6 | 0,2 | 0,1 | P | 0,6 | 0,4 |
| X | -5 | -2 | Y | ||||||
| P | 0,1 | 0,3 | 0,2 | 0,4 | P | 0,2 | 0,8 |
| X | -3 | -1 | Y | -3 | |||||
| P | 0,3 | 0,2 | 0,2 | 0,3 | P | 0,5 | 0,5 |
| X | -8 | -6 | -1 | Y | |||||
| P | 0,1 | 0,3 | 0,2 | 0,4 | P | 0,3 | 0,7 |
| X | -2 | -1 | Y | ||||||
| P | 0,1 | 0,5 | 0,2 | 0,2 | P | 0,7 | 0,3 |
| X | -3 | Y | |||||||
| P | 0,1 | 0,6 | 0,2 | 0,1 | P | 0,2 | 0,8 |
| X | -5 | Y | |||||||
| P | 0,2 | 0,3 | 0,1 | 0,4 | P | 0,4 | 0,6 |
| X | -3 | Y | |||||||
| P | 0,3 | 0,2 | 0,2 | 0,3 | P | 0,9 | 0,1 |
| X | -3 | -7 | Y | ||||||
| P | 0,1 | 0,2 | 0,3 | 0,4 | P | 0,3 | 0,7 |
(№ 21–40)
Даны две независимые дискретные случайные величины X и Y, которые заданы своими законами распределения. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение суммы этих случайных величин и математическое ожидание их произведения.
| X | Y | ||||||||||
| P | 0,3 | 0,2 | 0,4 | 0,1 | P | 0,3 | 0,2 | 0,4 | 0,1 |
| X | Y | ||||||||||
| P | 0,2 | 0,4 | 0,3 | 0,1 | P | 0,2 | 0,4 | 0,3 | 0,1 |
| X | Y | ||||||||||
| P | 0,2 | 0,2 | 0,5 | 0,1 | P | 0,1 | 0,5 | 0,3 | 0,1 |
| X | Y | ||||||||||
| P | 0,2 | 0,4 | 0,3 | 0,1 | P | 0,1 | 0,5 | 0,2 | 0,2 |
| X | Y | ||||||||||
| P | 0,1 | 0,2 | 0,5 | 0,2 | P | 0,1 | 0,4 | 0,2 | 0,3 |
| X | Y | ||||||||||
| P | 0,1 | 0,3 | 0,4 | 0,2 | P | 0,2 | 0,4 | 0,3 | 0,1 |
| X | Y | ||||||||||
| P | 0,2 | 0,3 | 0,1 | 0,4 | P | 0,2 | 0,3 | 0,4 | 0,1 |
| X | Y | ||||||||||
| P | 0,2 | 0,3 | 0,1 | 0,4 | P | 0,2 | 0,1 | 0,5 | 0,2 |
| X | Y | ||||||||||
| P | 0,1 | 0,2 | 0,4 | 0,3 | P | 0,2 | 0,3 | 0,4 | 0,1 |
| X | Y | ||||||||||
| P | 0,3 | 0,5 | 0,1 | 0,1 | P | 0,1 | 0,4 | 0,3 | 0,2 |
| X | Y | ||||||||||
| P | 0,1 | 0,2 | 0,2 | 0,5 | P | 0,1 | 0,3 | 0,2 | 0,4 |






