1. Перевірка правильності нульової гіпотези про значення генеральної середньої.
Приклад. Розбіжність вимірів діаметрів кульок X = xi є випадковою величиною, що має закон розподілу N (a; 4). При рівні значущості a = 0,01 перевірити правильність гіпотези 
мм, якщо альтернативна гіпотеза 
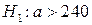мм, коли відомо, що 
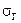= 4 мм і вибіркове середнє значення виміряних у 100 однотипних кульок 
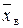= 225 мм.
Розв’язання. Оскільки 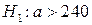мм, будується правобічна критична область. Для цього необхідно знайти критичну точку і побудувати правобічну критичну область. Для знаходження критичної точки застосовуємо відомий вираз:
.
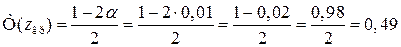За значенням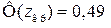 
і скориставшись таблицею знаходимо 
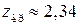. Отже, правобічна критична область матиме вигляд, зображений на рис. 126.
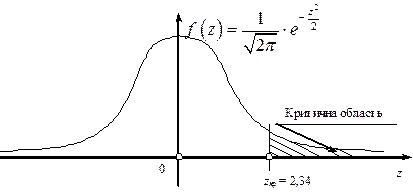
Рис. 126
Обчислимо спостережуване значення критерію за формулою (451)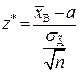 
. Оскільки 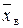= 225 мм, а = 240 мм, 
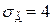мм, n = 100, маємо
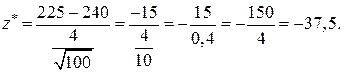
Висновок. Оскільки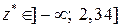 
, то немає підстав для відхилення нульової гіпотези 
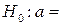240 мм.
Отже, нульова гіпотеза приймається.
Приклад. Проведено 10 незалежних експериментів над випадковою величиною Х, що має нормальний закон розподілу з невідомими значеннями а, s. Наслідки експериментів подано у вигляді статистичного ряду:
| xi | 2,5 | –2,3 | 1,9 | –2,1 | 2,4 | 2,3 | –2,5 | 1,5 | –1,7 | |
| ni |
При рівні значущості a = 0,001 перевірити правильність нульової гіпотези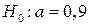 
, при альтернативній гіпотезі 
.
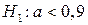Розв’язання. Запишемо статистичний ряд у вигляді статистичного розподілу й обчислимо ,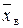 
:
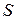| xi | –2,5 | –2,3 | –2,1 | –1,7 | 1,5 | 1,9 | 2,3 | 2,4 | 2,5 | |
| ni |
.
. 
.
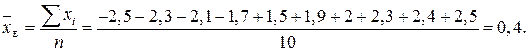
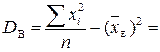
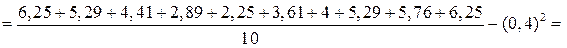
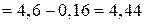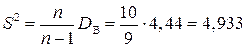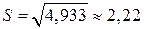При альтернативній гіпотезі 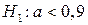будується лівобічна критична область. Для цього необхідно знайти критичну точку, застосовуючи статистичний критерій (451). За таблицею (додаток 6) знаходимо значення
= 
.
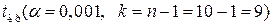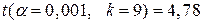Оскільки щільність ймовірностей для розподілу Стьюдента є парною, то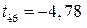 
.
Критична область показана на рис. 127.
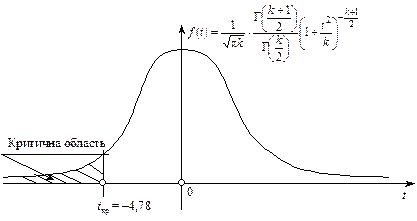
Рис. 127
Обчислимо спостережуване значення критерію:
.
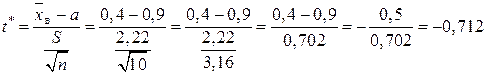Висновок. Оскільки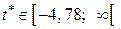 
, то немає підстав відхилити .
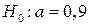Приклад. Реалізувавши вибірку з генеральної сукупності, ознака якої Х має нормальний закон розподілу, дістали статистичний розподіл:
| xi | |||||||||
| ni |
При рівні значущості a = 0,01 перевірити правильність нульової гіпотези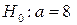 
, якщо альтернативна гіпотеза 
.
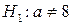Розв’язання. Обчислимо значення , :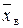
.
.
. 
.
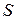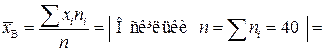
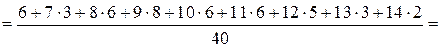
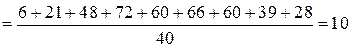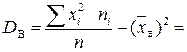
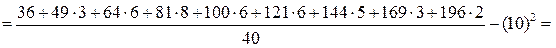
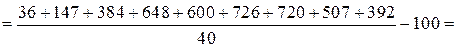
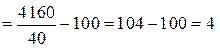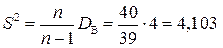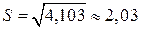При альтернативній гіпотезі 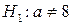будуємо двобічну критичну область. Враховуючи, що sГ є невідомою величиною, для побудови цієї області беремо статистичний критерій (452).
Оскільки критичні точки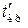 
і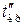 
симетричні відносно нуля і при цьому 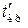= – 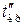, знаходимо за таблицею (додаток 6) :
.
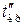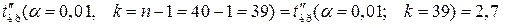Тоді 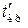= – 2,7.
Двобічна критична область зображена на рис. 128.
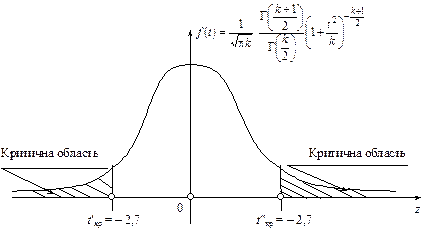
Рис. 128
Обчислимо спостережуване значення критерію:
.
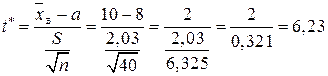Висновок. Оскільки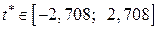 
, то немає підстав приймати .
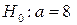Приклад. З генеральної сукупності, ознака якої Х має закон розподілу N (a; 5), реалізована вибірка і побудовано статистичний розподіл:
| xi | 10,9 | 11,2 | 11,3 | 11,5 | 11,6 | 11,8 | 11,9 | |
| ni |
При рівні значущості a = 0,01 перевірити правильність нульової гіпотези
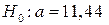при альтернативній гіпотезі
.
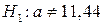Розв’язання. Обчислимо значення 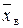. Оскільки 
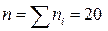, то дістанемо
.
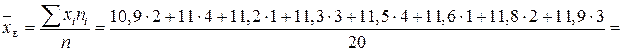
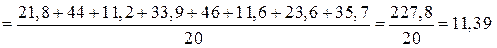При альтернативній гіпотезі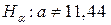 
будується двобічна критична область. Враховуючи те, що відоме значення 
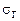= 5, для знаходження критичних точок скористаємося статистичним критерієм 
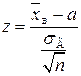, що має закон розподілу N (0; 1).
Критична точка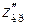 
визначається з рівності
.
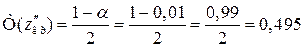За значенням функції Лапласа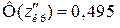 
знаходимо 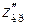= 2,58.
Оскільки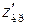 
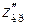= – , то маємо 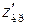= – 2,58.
Двобічна критична область зображена на рис. 129.
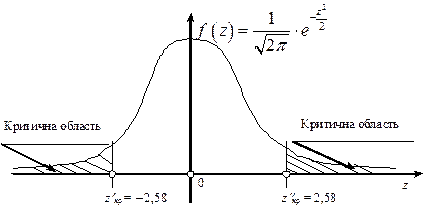
Рис. 129
Обчислимо спостережуване значення критерію
.
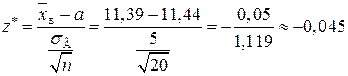Висновок. Оскільки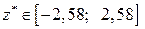 
, немає підстав відхиляти .
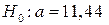Приклад. Реалізувавши вибірку з генеральної сукупності, елементами якої є однотипні заготівки, довжина яких Х є випадковою величиною з нормальним законом розподілу, дістали статистичний розподіл:
| xi | 6,5 | 8,5 | 10,5 | 12,5 | 14,5 | 16,5 |
| ni |
Якщо рівень значущості a = 0,001, перевірити правильність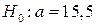 
при альтернативній гіпотезі 
.
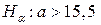Розв’язання. Обчислимо значення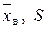 
. Оскільки 
, то маємо
;
.
.
. 
.
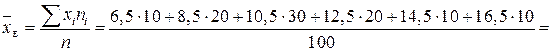
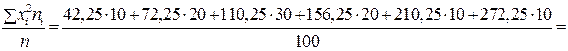
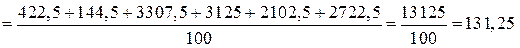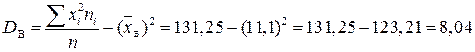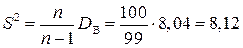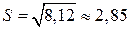Оскільки обсяг вибірки великий (n = 100 > 40), статистичний критерій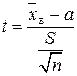 
наближатиметься до закону розподілу N (0; 1). Тому для визначення критичної точки 
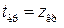застосовуємо рівність
.
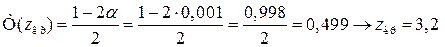Правобічна критична область матиме такий вигляд (рис. 130):
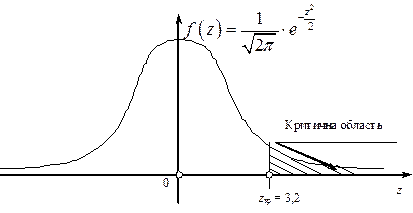
Рис. 130
Обчислимо спостережуване значення критерію
.
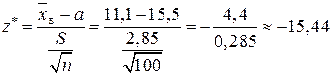Висновок. Оскільки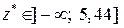 
, то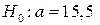 
приймається.
