Практичне заняття 13. Двовимірна дискретна випадкова величина

Задача. Дискретна двомірна випадкова величина 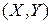задана законом розподілу

–1	0,04	2 а	0,1
	0,05	0,2	0,1
	а	0,05	0,01

Знайти: 1) параметр а; 2) закони розподілу випадкових величин та ; 3) функцію розподілу ; 4) функції розподілу 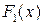та ; 5) ; 6) та ; 7) та ; 8) ; 9) .

Розв’язання. 1) Параметр а знаходимо з умови , тобто

, або .

2) Знайдемо значення

, ,

і запишемо ряд розподілу випадкової величини

	0,24	0,55	0,21

Аналогічно знаходимо

, ,

і запишемо ряд розподілу випадкової величини

	–1
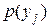
	0,44	0,35	0,21

3) Використовуючи формулу , знайдемо двомірну функцію розподілу , , , , ,

, ,

,

,

,

.

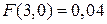4) Скориставшись законами розподілу випадкових величин та , знайдемо 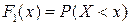та :

, ,

, ;

, ,

, .

5)

.

6) Для обчислення та скористаємось рядами розподілу випадкових величин та :

,

.

7) Обчислюємо дисперсії випадкових величин та :

8) Для обчислення коефіцієнта кореляції 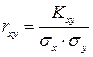необхідно спочатку знайти , та :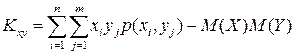

, ,

.

Підставивши отримані значення в формулу, знайдемо коефіцієнт кореляції .

9) . Обчислимо значення умовних ймовірностей :

, , .

Знайдемо умовне математичне сподівання

.

 

Задача 2. Дискретна двомірна випадкова величина 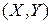задана законом розподілу:

	–2	–1
	0,03	0,07	0,25	0,08
	0,04	0,05	0,1	0,15
	0,02	0,01		0,2

Знайти: 1) закони розподілу випадкових величин та ; 2) функцію розподілу ; 3) функції розподілу 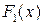та ; 4) .

ПРАКТИЧНЕ ЗАНЯТТЯ 14. ДВОВИМІРНА НЕПЕРЕРВНА

ВИПАДКОВА ВЕЛИЧИНА

 

Задача. Двовимірна випадкова величина 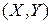має щільність розподілу в області і поза областю.

Знайти: 1) параметр а; 2) ймовірність потрапити в область .

Розв’язання. 1) Параметр а знаходимо з умови, що 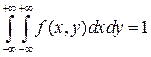, тобто

.

Звідки .

2) .

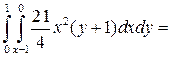
Задача. Двовимірна випадкова величина 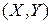має щільність розподілу в прямокутній області і по за областю.

Знайти: 1) функцію розподілу ; 2) та ; 3) та ; 4) .

Розв’язання. 1) За означенням 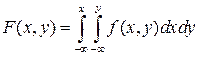, тоді якщо або ;

, якщо i якщо , .

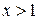2) Для того щоб знайти та потрібно визначити та . Знайдемо ці щiльностi розподiлiв за формулами: , .

,

.

Математичні сподівання знаходимо за формулами

,

.

3) ,

.

4) Для знаходження коефiцiєнта кореляцiï 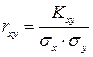спочатку обчислимо , та

.

, .

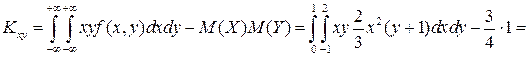
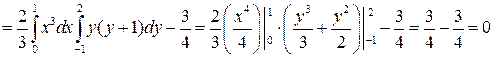Тодi .

ПРАКТИЧНЕ ЗАНЯТТЯ 15. СТАТИСТИЧНІ ОЦІНКИ

ПАРАМЕТРІВ РОЗПОДІЛУ

Приклад. За заданим дискретним статистичним розподілом вибірки

X = xi	–6	–4	–2
ni
Wi	0,05	0,1	0,15	0,2	0,4	0,1

потрібно:

1. Побудувати F ^*(x) і зобразити її графічно;

2. Накреслити полігони частот і відносних частот.

Розв’язання. Згідно з означенням та властивостями F ^*(x) має такий вигляд:

Графічне зображення F ^*(x) подано на рис. 106.

 

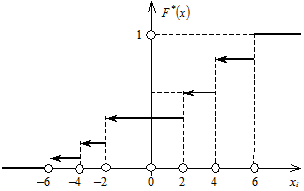
Рис. 106

Полігони частот та відносних частот зображено на рис.107, 108.

Рис. 107

Рис. 108

 

Приклад. За заданим статистичним розподілом вибірки

X = xi	2,5	4,5	6,5	8,5	10,5
ni

потрібно:

1) обчислити , , ;

2) знайти Mo^*, Me^*;

3) обчислити R, V.

Розв’язання. Оскільки , то згідно з формулами (354), (357), (358) дістанемо:

.

Для обчислення визначається

Тоді .

= 5,16.

= 2,27.

Mo^* = 6,5; 8,5.

Отже, наведений статистичний розподіл вибірки буде двомодaльним. Me^* = 6,5, оскільки варіанта х = 6,5 поділяє варіаційний ряд 2,5; 4,5; 6,5; 8,5; 10,5 на дві частини: 2,5; 4,5 і 8,5; 10,5, які мають однакову кількість варіант.